Entropy Search for Information-Efficient Global Optimization

概
主要内容
- 的估计
- 的估计

Hennig P, Schuler C J. Entropy search for information-efficient global optimization[J]. Journal of Machine Learning Research, 2012, 13(1): 1809-1837.

@article{hennig2012entropy,

title={Entropy search for information-efficient global optimization},

author={Hennig, Philipp and Schuler, Christian J},

journal={Journal of Machine Learning Research},

volume={13},

number={1},

pages={1809--1837},

year={2012}}

概

贝叶斯优化中的 Entropy Search (EI) 方法.

主要内容

这篇文章关注的是

\[\max_{x \in I} \:f(x),
\]

的问题, 且假设定义域\(I\)是有界的.

一般, 通过高斯过程定义\(f(x)\)的概率替代函数, 假设

\[f(x) \sim \mathcal{N}(u_0(x), k(x,x)),\\
y = f(x) + \epsilon, \: \epsilon \sim \mathcal{N}(0, \sigma^2).
\]

在已经观测到\(X = \{x_1, \ldots, x_T\}\)以及\(Y = \{y_1, \ldots, y_T\}\)的基础上, 我们可以求得\(f(x^*)\)的后验分布为以

\[\mu (x^*) = \mu_0(x^*) + k(x^*, X)^T [k(X, X) + \sigma I]^{-1}(Y-u_0(X)) \\
\sigma_*^2(x^*)=k(x^*, x^*) - k(x^*, X)^T (k(X,X)+\sigma I)^{-1}k(x^*,X)
\]

为均值和方差的正态分布.

我们的目的是在已有这些条件的基础上, 寻找下一个(或多个)评估点.

定义:

\[\tag{1}
p_{min}(x) =p[x = \arg \min f(x)] = \int_{ f:I \rightarrow R} p(f) \prod_{\tilde{x} \in I, \tilde{x} \not = x} \theta[f(\tilde{x})-f(x)] \mathrm{d}f,
\]

其中\(\theta(x) = 1, x\ge0, else \: 0\). \(\prod\)的部分在针对连续型的定义域时需要特别的定义. 显然(1)表示\(x\)为最小值点的概率.

再定义损失函数(当然损失函数不选择KL散度也是可以的, 但这是EI的名字的由来):

\[\tag{2}
\mathcal{L}(p_{min}) = \mathcal{L}_{KL}(p_{min})=-\int_Ip_{min}(x) \log \frac{p_{min}(x)}{b(x)} \mathrm{d}x.
\]

当我们选择\(b(x)\)为\(I\)上的均匀分布的时候, 当我们最小化\(\mathcal{L}\)的时候, \(p_{min}\)会趋向Dirac分布(即某个点处的概率密度为无穷, 其余为0, 显然, 该点我们有足够的信心认为其是\(f(x)\)的最小值点).

但是这样还不够, 我们进一步关心其期望损失(最小化):

\[\tag{3}
\langle \mathcal{L} \rangle_{x} = \int p(y|x) \mathcal{L}(p_{min} (\cdot|Y, X, y, x)) \mathrm{d}y.
\]

通过最小化(3)，我们可以获得接下来的评估点.

接下来的问题是如果去估计.

\(p_{min}\)的估计

比较麻烦的是\(\prod\)的部分, 策略是挑选\(N\)个点\(\tilde{x} = \{\tilde{x}_1, \ldots, \tilde{x}_N\}\). 一种是简单粗暴的网格的方式, 但是这种方式往往需要较大的\(N\), 另一种是给定一个测度\(u\), 根据已有的观察\((X, Y)\), 通过\(u(X, Y)\)采样\(\tilde{x}\). 一个好的\(u\)应该在使得令损失能够产生较大变化的区域多采样点, 针对本文的情况应该在\(p_{min}\)值比较高的地方多采样点.

文中给了俩种方法, 一种直接的方法是\(p_{min}\)可以用蒙特卡洛积分去逼近,

一下是我猜想的用MC积分的方式(文中未给出具体的形式)"

根据一定策略选取\(\tilde{x}\);
重复J次:

根据概率\(p(f)\)采样\(f(\tilde{x}), f(x)\),
计算\(\prod\)部分

取平均

作者选择的是 Expectation Propagation (EP）的方法, 这种方法能够估计出\(\tilde{x}_i, i=1,\ldots,N\)处的概率\(q_{min}(\tilde{x_i})\): \(f_{min}\)存在于以\(\tilde{x}_i\)为"中心"的一定范围内(文中用step)的概率. 当\(N\)足够的的时候, 这个step正比于\((Nu(\tilde{x}_i))^{-1}\), 则:

\[p_{min}(x) \approx \frac{q_{min}(x_i)Nu(\tilde{x}_i)}{Z_u}, \: Z_u=\int u(x) \mathrm{d}x, \: x_i = \arg \min_{x_i \in \tilde{x}} \|x-x_i\|.
\]

这样我们就完成了\(p_{min}\)的估计, 一个更加好的性质是\(q_{min}\)关于\(\mu, \sigma_*\)的导数是有解析表达式的, 且\(Z_u\)是不必计算的(后续最小化过程中可以省略掉).

\(\mathcal{L}_{KL}\)的估计

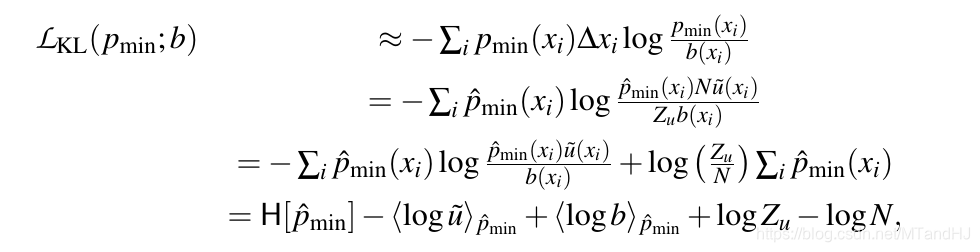
其中\(\hat{p}_{min}=q_{min}\).

\(\langle \Delta \mathcal{L} \rangle\)

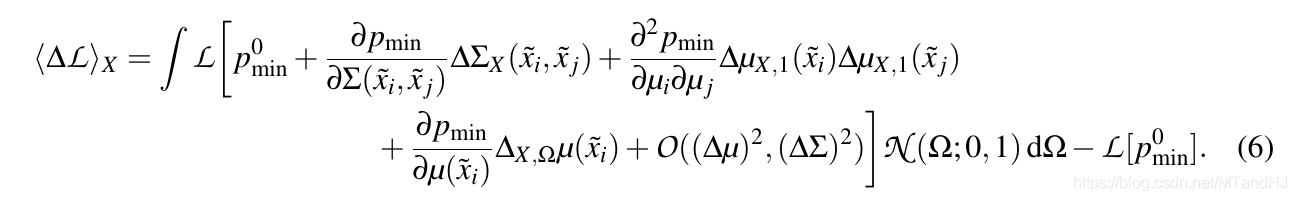
\(\arg \min_X \langle \mathcal{L} \rangle_X\) 用最小化一阶近似替代, 积分可以用MC积分逼近.

最后给出算法: