Algorithm：MD5算法原理说明

MD5算法实现：

输入：不定长度信息（要加密的信息）

输出：固定长度128-bits。由四个32位分组组成，将这四个32位分组级联后将生成一个128位散列值。

基本方式为：求余、取余、调整长度、与链接变量进行循环运算。得出结果。

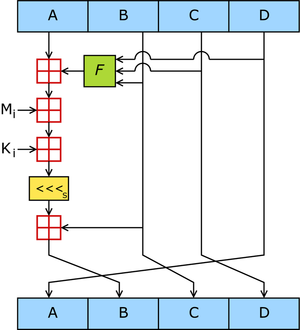
流程图：

1.填充

在MD5算法中，首先需要对输入信息进行填充，使其位长对512求余的结果等于448，并且填充必须进行，即使其位长对512求余的结果等于448。

因此，信息的位长（Bits Length）将被扩展至N*512+448，N为一个非负整数，N可以是零。
填充的方法如下：
1) 在信息的后面填充一个1和无数个0，直到满足上面的条件时才停止用0对信息的填充。
2) 在这个结果后面附加一个以64位二进制表示的填充前信息长度（单位为Bit），如果二进制表示的填充前信息长度超过64位，则取低64位。
经过这两步的处理，信息的位长=N*512+448+64=(N+1）*512，即长度恰好是512的整数倍。这样做的原因是为满足后面处理中对信息长度的要求。

2. 初始化变量（变量值一般不变）

初始的128位值为初试链接变量，这些参数用于第一轮的运算，以大端字节序来表示，他们分别为：

(在程序中变量A、B、C、D的值分别为0x67452301，0xEFCDAB89，0x98BADCFE，0x10325476)

A=0x01234567，

B=0x89ABCDEF，

C=0xFEDCBA98，

D=0x76543210。
（每一个变量给出的数值是高字节存于内存低地址，低字节存于内存高地址，即大端字节序。）

3. 处理分组数据

每一分组的算法流程如下：
（1）第一分组需要将上面四个链接变量复制到另外四个变量中：A到a，B到b，C到c，D到d。

（2）从第二分组开始的变量为上一分组的运算结果，即A = a， B = b， C = c， D = d。

主循环有四轮（MD4只有三轮），每轮循环都很相似。第一轮进行16次操作。每次操作对a、b、c和d中的其中三个作一次非线性函数运算，然后将所得结果加上第四个变量，文本的一个子分组和一个常数。再将所得结果向左环移一个不定的数，并加上a、b、c或d中之一。最后用该结果取代a、b、c或d中之一。

一个MD5运算由类似的64次循环构成，分成4组16次。

F ：一个非线性函数，一个函数运算一次

Mi ：表示一个 32-bits 的输入数据

Ki：表示一个 32-bits 常数，用来完成每次不同的计算。

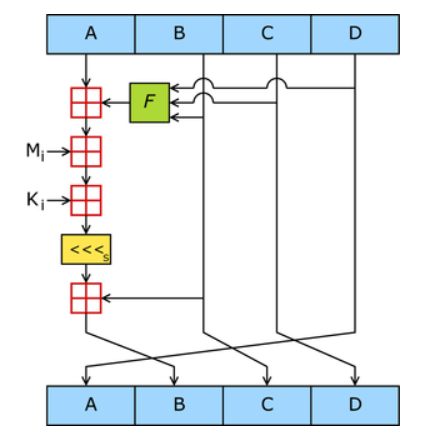
以下是每次操作中用到的四个非线性函数（每轮一个）。
F( X ,Y ,Z ) = ( X & Y ) | ( (~X) & Z )
G( X ,Y ,Z ) = ( X & Z ) | ( Y & (~Z) )
H( X ,Y ,Z ) =X ^ Y ^ Z
I( X ,Y ,Z ) =Y ^ ( X | (~Z) )
（&是与（And），|是或（Or），~是非（Not），^是异或（Xor））
这四个函数的说明：如果X、Y和Z的对应位是独立和均匀的，那么结果的每一位也应是独立和均匀的。
F是一个逐位运算的函数。即，如果X，那么Y，否则Z。函数H是逐位奇偶操作符。
假设Mj表示消息的第j个子分组（从0到15），常数ti是4294967296*abs( sin(i) ）的整数部分，i 取值从1到64，单位是弧度。（4294967296=2^(32)）

现定义：
FF(a ,b ,c ,d ,Mj ,s ,ti ) 操作为 a = b + ( (a + F(b,c,d) + Mj + ti) << s)
GG(a ,b ,c ,d ,Mj ,s ,ti ) 操作为 a = b + ( (a + G(b,c,d) + Mj + ti) << s)
HH(a ,b ,c ,d ,Mj ,s ,ti) 操作为 a = b + ( (a + H(b,c,d) + Mj + ti) << s)
II(a ,b ,c ,d ,Mj ,s ,ti) 操作为 a = b + ( (a + I(b,c,d) + Mj + ti) << s)

注意：“<<”表示循环左移位，不是左移位。

这四轮（共64步）是：
第一轮
FF(a ,b ,c ,d ,M0 ,7 ,0xd76aa478 )
FF(d ,a ,b ,c ,M1 ,12 ,0xe8c7b756 )
FF(c ,d ,a ,b ,M2 ,17 ,0x242070db )
FF(b ,c ,d ,a ,M3 ,22 ,0xc1bdceee )
FF(a ,b ,c ,d ,M4 ,7 ,0xf57c0faf )
FF(d ,a ,b ,c ,M5 ,12 ,0x4787c62a )
FF(c ,d ,a ,b ,M6 ,17 ,0xa8304613 )
FF(b ,c ,d ,a ,M7 ,22 ,0xfd469501)
FF(a ,b ,c ,d ,M8 ,7 ,0x698098d8 )
FF(d ,a ,b ,c ,M9 ,12 ,0x8b44f7af )
FF(c ,d ,a ,b ,M10 ,17 ,0xffff5bb1 )
FF(b ,c ,d ,a ,M11 ,22 ,0x895cd7be )
FF(a ,b ,c ,d ,M12 ,7 ,0x6b901122 )
FF(d ,a ,b ,c ,M13 ,12 ,0xfd987193 )
FF(c ,d ,a ,b ,M14 ,17 ,0xa679438e )
FF(b ,c ,d ,a ,M15 ,22 ,0x49b40821 )
第二轮
GG(a ,b ,c ,d ,M1 ,5 ,0xf61e2562 )
GG(d ,a ,b ,c ,M6 ,9 ,0xc040b340 )
GG(c ,d ,a ,b ,M11 ,14 ,0x265e5a51 )
GG(b ,c ,d ,a ,M0 ,20 ,0xe9b6c7aa )
GG(a ,b ,c ,d ,M5 ,5 ,0xd62f105d )
GG(d ,a ,b ,c ,M10 ,9 ,0x02441453 )
GG(c ,d ,a ,b ,M15 ,14 ,0xd8a1e681 )
GG(b ,c ,d ,a ,M4 ,20 ,0xe7d3fbc8 )
GG(a ,b ,c ,d ,M9 ,5 ,0x21e1cde6 )
GG(d ,a ,b ,c ,M14 ,9 ,0xc33707d6 )
GG(c ,d ,a ,b ,M3 ,14 ,0xf4d50d87 )
GG(b ,c ,d ,a ,M8 ,20 ,0x455a14ed )
GG(a ,b ,c ,d ,M13 ,5 ,0xa9e3e905 )
GG(d ,a ,b ,c ,M2 ,9 ,0xfcefa3f8 )
GG(c ,d ,a ,b ,M7 ,14 ,0x676f02d9 )
GG(b ,c ,d ,a ,M12 ,20 ,0x8d2a4c8a )
第三轮
HH(a ,b ,c ,d ,M5 ,4 ,0xfffa3942 )
HH(d ,a ,b ,c ,M8 ,11 ,0x8771f681 )
HH(c ,d ,a ,b ,M11 ,16 ,0x6d9d6122 )
HH(b ,c ,d ,a ,M14 ,23 ,0xfde5380c )
HH(a ,b ,c ,d ,M1 ,4 ,0xa4beea44 )
HH(d ,a ,b ,c ,M4 ,11 ,0x4bdecfa9 )
HH(c ,d ,a ,b ,M7 ,16 ,0xf6bb4b60 )
HH(b ,c ,d ,a ,M10 ,23 ,0xbebfbc70 )
HH(a ,b ,c ,d ,M13 ,4 ,0x289b7ec6 )
HH(d ,a ,b ,c ,M0 ,11 ,0xeaa127fa )
HH(c ,d ,a ,b ,M3 ,16 ,0xd4ef3085 )
HH(b ,c ,d ,a ,M6 ,23 ,0x04881d05 )
HH(a ,b ,c ,d ,M9 ,4 ,0xd9d4d039 )
HH(d ,a ,b ,c ,M12 ,11 ,0xe6db99e5 )
HH(c ,d ,a ,b ,M15 ,16 ,0x1fa27cf8 )
HH(b ,c ,d ,a ,M2 ,23 ,0xc4ac5665 )
第四轮
II(a ,b ,c ,d ,M0 ,6 ,0xf4292244 )
II(d ,a ,b ,c ,M7 ,10 ,0x432aff97 )
II(c ,d ,a ,b ,M14 ,15 ,0xab9423a7 )
II(b ,c ,d ,a ,M5 ,21 ,0xfc93a039 )
II(a ,b ,c ,d ,M12 ,6 ,0x655b59c3 )
II(d ,a ,b ,c ,M3 ,10 ,0x8f0ccc92 )
II(c ,d ,a ,b ,M10 ,15 ,0xffeff47d )
II(b ,c ,d ,a ,M1 ,21 ,0x85845dd1 )
II(a ,b ,c ,d ,M8 ,6 ,0x6fa87e4f )
II(d ,a ,b ,c ,M15 ,10 ,0xfe2ce6e0 )
II(c ,d ,a ,b ,M6 ,15 ,0xa3014314 )
II(b ,c ,d ,a ,M13 ,21 ,0x4e0811a1 )
II(a ,b ,c ,d ,M4 ,6 ,0xf7537e82 )
II(d ,a ,b ,c ,M11 ,10 ,0xbd3af235 )
II(c ,d ,a ,b ,M2 ,15 ,0x2ad7d2bb )
II(b ,c ,d ,a ,M9 ,21 ,0xeb86d391 )

所有这些完成之后，将a、b、c、d分别在原来基础上再加上A、B、C、D。
即a = a + A，b = b + B，c = c + C，d = d + D
然后用下一分组数据继续运行以上算法。

4. 输出

最后的输出是a、b、c和d的级联。

文章转载至：https://blog.csdn.net/hla199106/article/details/45129963