题解 CF613E Puzzle Lover

解题思路

其实仔细观察我们可以发现路径一定是一个类似于下图的一个左括号之后中间随便反复曲折，然后右边在来一个右括号。

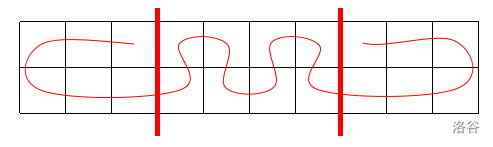
然后对于两个括号形状的东西其实是可以利用 Hash 来判等特殊处理的。

对于中间的部分直接 DP ：

\(f_{i,j,k,0/1}\) 表示第 \(i\) 行，第 \(j\) 列，当前扫到了询问路径的第 \(k\) 个位置，并且是否可以向上或者下转移。

然后优先处理一下左括号形，这里可以维护两个 Hash 分别存储正反的 Hash 值进行判等。

接下来就 DP 处理中间曲折的部分（ \(ch\) 为字符矩阵， \(s\) 为目标字符串），对于 \(ch_{i,j}=s_k\) 的情况进行转移，转移方程如下：

\[f_{i,j,k,0}=f_{i,j,k,0}+f_{i,j-1,k-1,0}+f_{i,j-1,k-1,1}
\]

\[f_{i,j,k,1}=f_{i,j,k,1}+f_{i\;xor\;1,j,k-1,0}
\]

注意转移的时候为了防止当前状态对于之后状态造成过多影响，应该把 k 的循环放在最外层。

对于一个路径而言因为是有向的，因此我们把字符串翻转之后再做一边 DP 就好了。

code

#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define f() cout<<"Pass"<<endl
using namespace std;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
const int N=2e3+10,mod=1e9+7;
const ull base=1331ull;
ull has[N],pre[2][N],suf[2][N],p[N<<1];
int n,m,ans,f[2][N][N<<1][2];
char ch[2][N],s[N<<1];
void Hash()
{
	for(int i=0;i<=1;i++)
		for(int j=1;j<=n;j++)
			pre[i][j]=pre[i][j-1]*base+ch[i][j];
	for(int i=0;i<=1;i++)
		for(int j=n;j>=1;j--)
			suf[i][j]=suf[i][j+1]*base+ch[i][j];
}
ull get_suf(int x,int l,int r){return suf[x][l]-suf[x][r+1]*p[r-l+1];}
ull get_pre(int x,int l,int r){return pre[x][r]-pre[x][l-1]*p[r-l+1];}
ull get_hash(int l,int r){return has[r]-has[l-1]*p[r-l+1];}
void add(int &x,int y){x+=y;if(x>=mod)x-=mod;}
void solve()
{
	Hash();
	for(int i=0;i<=1;i++)
		for(int j=1;j<=n;j++)
		{
			f[i][j][1][0]=(ch[i][j]==s[1]);
			for(int k=2;k<=min(j,m/2);k++)
				if((get_hash(1,k)==get_suf(i^1,j-k+1,j))&&(get_hash(k+1,k<<1)==get_pre(i,j-k+1,j)))
					f[i][j][k<<1][1]=1;
		}
	for(int k=1;k<=m;k++)
		for(int i=0;i<=1;i++)
			for(int j=1;j<=n;j++)
				if(ch[i][j]==s[k])
				{
					add(f[i][j][k][0],f[i][j-1][k-1][0]+f[i][j-1][k-1][1]);
		        	add(f[i][j][k][1],f[i^1][j][k-1][0]);
				}
	for(int i=0;i<=1;i++)
		for(int j=1;j<=n;j++)
			for(int k=0;k<=m;k++)
				if(m-k!=2&&((k&1)==(m&1)))
					add(ans,(f[i][j][k][1]+f[i][j][k][0])*(m==k||(j+(m-k)/2<=n&&get_pre(i,j+1,j+(m-k)/2)==get_hash(k+1,k+(m-k)/2)&&get_suf(i^1,j+1,j+(m-k)/2)==get_hash(k+(m-k)/2+1,m))));
}
void Special_Judge1()
{
	for(int i=0;i<=1;i++)
		for(int j=1;j<=n;j++)
			ans-=(ch[i][j]==s[1]);
}
void Special_Judge2()
{
	for(int i=0;i<=1;i++)
		for(int j=1;j<=n;j++)
			ans-=(ch[i][j]==s[1]&&ch[i^1][j]==s[2]);
}
signed main()
{
	scanf("%s%s%s",ch[0]+1,ch[1]+1,s+1);
	n=strlen(ch[0]+1);	m=strlen(s+1);
	p[0]=1;	for(int i=1;i<=m;i++)	p[i]=p[i-1]*base;
	for(int i=1;i<=m;i++)	has[i]=has[i-1]*base+s[i];
	if(m==1)	Special_Judge1();
	if(m==2)	Special_Judge2();
	solve();
	memset(f,0,sizeof(f));
	for(int i=0;i<=1;i++)	reverse(ch[i]+1,ch[i]+n+1);
	solve();
	printf("%lld",(ans+mod)%mod);
	return 0;
}