数据源：

任意五行两列

目标：

将原排列顺序颠倒

操作过程：

【转换】》【反转行】

　　

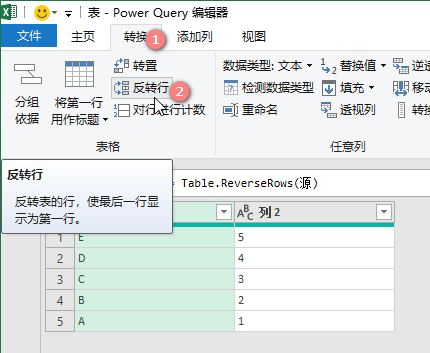
M公式：

　　 = Table.ReverseRows( 表 )

扩展：

　　反转列表：= List.Reverse( 列表 )

　　反转字符串：= Text.Reverse( "字符串" )

Table.ReverseRows反转…Reverse…（Power Query 之 M 语言）的更多相关文章

  1. Table.Sort排序…Sort（Power Query 之 M 语言）

    数据源: 任意查询表 目标: 对其中一列数据进行排序 操作过程: 选取对象>[主页]>[排序]>[升序排序] 选取对象>[主页]>[排序]>[降序排序] M公式: ...

  2. M函数目录（Power Query 之 M 语言）

    2021-12-11更新 主页(选项卡) 管理列(组) 选择列 选择列Table.SelectColumns 删除列 删除列Table.RemoveColumns 删除其他列Table.SelectC ...

  3. Excel.CurrentWorkbook数据源（Power Query 之 M 语言）

    数据源: 任意超级表 目标: 将超级表中的数据加载到Power Query编辑器中 操作过程: 选取超级表中任意单元格(选取普通表时会自动增加插入超级表的步骤)>数据>来自表格/区域 M公 ...

  4. 自定义函数（Power Query 之 M 语言）

    数据源: 任意工作簿 目标: 使用自定义函数实现将数据源导入Power Query编辑器 操作过程: PowerQuery编辑器>主页>新建源>其他源>空查询 编辑栏内写入公式 ...

  5. M语言的写、改、删（Power Query 之 M 语言）

    M语言基本上和其他语言一样,用敲键盘的方式写入.修改.删除,这个是废话. M语言可以在[编辑栏]或[高级编辑器]里直接写入.修改.删除,这个也是废话. M语言还有个地方可以写入.修改.删除,就是[自定 ...

  6. M语言的藏身之地（Power Query 之 M 语言）

    M函数和M公式是Power Query专用的函数与公式,M代码是Power Query专用的用于实现查询功能的代码.M函数公式和M代码统称M语言. 查看M公式:[编辑栏] 查看方法:在Power Qu ...

  7. Table.ReorderColumns移动…Reorder…（Power Query 之 M 语言）

    数据源: 至少两列 目标: 列顺序重新排列 操作过程: 选取待移动的列>鼠标拖放列标题 选取待移动的列>[转换]>[移动]>选取 M公式:  = Table.ReorderCo ...

  8. Table.FillDown填充Table.Fill…（Power Query 之 M 语言）

    数据源: 任意列中包含空单元格 目标: 将空单元格填充为其上或其下单元格中的内容 操作过程: 选取指定列>[转换]>[填充]>[向下] 选取指定列>[转换]>[填充]&g ...

  9. Table.RowCount行列计数…Count（Power Query 之 M 语言）

    数据源: 任意五行两列 目标: 计算行数(包括空行) 操作过程: [转换]>[对行进行计数] M公式:  = Table.RowCount( 表 ) 扩展: 对表中列进行计数:= Table.C ...

随机推荐

  1. [luogu7831]Travelling Merchant

    考虑不断找到以下两种类型的边,并维护答案: 1.终点出度为0的边,那么此时即令$ans_{x}=\min(ans_{x},\max(r,ans_{y}-p))$​ 2.(在没有"终点出度为0 ...

  2. 【JavaSE】JDK配置

    Java开发环境配置 2020-09-10  08:32:20  by冲冲 1. Windows7安装JDK 1.1 下载JDK ① 下载地址:http://www.oracle.com/techne ...

  3. 洛谷 P5249 - [LnOI2019]加特林轮盘赌（期望 dp+高斯消元）

    题面传送门 期望真 nm 有意思,所以蒟蒻又来颓期望辣 先特判掉 \(P_0=0\) 的情况,下面假设 \(P_0\ne 0\). 首先注意到我们每次将加特林对准一个人,如果这个人被毙掉了,那么相当于 ...

  4. SAM 做题笔记（各种技巧，持续更新，SA）

    SAM 感性瞎扯. 这里是 SAM 做题笔记. 本来是在一篇随笔里面,然后 Latex 太多加载不过来就分成了两篇. 标 * 的是推荐一做的题目. trick 是我总结的技巧. I. P3804 [模 ...

  5. JSOI2021 游记

    Day 0 - 2021.4.9 写一波最近的事情吧( 3 月 20 号出头 cnblogs 抽风,说 25 号恢复来着,我就囤了一堆博客在本地准备 25 号发,结果到时候就懒得动了.干脆越屯越多,省 ...

  6. NOIP2020 模拟赛 B 组 Day6

    非常巧妙的一场模拟赛,比较偏向于 Atcoder 的风格,考场上做出了 A .C 两题. A. 礼物购买 排完序后一个个礼物地枚举时间复杂度是\(\Theta(nm)\)的,不能接受.但是注意到,若当 ...

  7. FVCOM编译过程详解

    本文目的旨在介绍fvcom编译的全过程,顺便介绍linux中make命令的文件写法和一般的编程过程简述一下. 1.编程过程 编程,一般就是编写可执行程序过程.这个过程主要是源文件生成中间代码文件,再到 ...

  8. 学习资源 Docker从入门到实践 pdf ，docker基础总结导图

    学习资源 Docker从入门到实践 pdf ,docker基础总结导图 Docker从入门到实践 pdf 云盘地址:https://pan.baidu.com/s/1vYyxlW8SSFSsMuKaI ...

  9. Python爬虫3大解析库使用导航

    1. Xpath解析库 2. BeautifulSoup解析库 3. PyQuery解析库

  10. cmd查看同一个局域网内电脑IP

    win+R,cmd  #快速打开cmd窗口 net view  #查看本地局域网内开启了哪些计算机共享  运行后可以看到已共享的计算机名称 net view ip  #查看对方局域网内开启了哪些共享 ...