经典串匹配算法（KMP）解析

一.问题重述

现有字符串S1，求S1中与字符串S2完全匹配的部分，例如：

S1 = "ababaababc"

S2 = "ababc"

那么得到匹配的结果是5（S1中的"ababc"的a的位置），当然如果S1中有多个S2也没关系，能找到第一个就能找到第二个。。

-------

最容易想到的方法自然是双重循环按位比对（BF算法），但在最坏的情况下BF算法的时间复杂度达到了m * n，这在实际应用中是不可接受的，于是某3个人想出来了KMP算法（KMP是三个人的名字。。）

二.KMP算法具体过程

（先不要着急想看KMP算法的官方定义，很难看懂的，所以这里干脆不给定义了。。）

认真审视一下S2 = "ababc"，很重要的一点是：开头出现了ab，中间部分又出现了ab（先记住这个细节）

现在假定一个时刻：

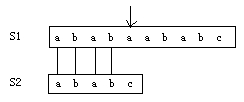
此时abab部分匹配成功，S1的位置指针指向了a，当前正在做的事情是a与c比对，结果是匹配失败

• 如果是BF算法，那么下一步是S1的位置指针回溯到第二位的b，S2的位置指针重置到开头的a，然后b与a比对，然后。。
• 如果是KMP算法，那么下一步是S1位置指针不变（指向a），然后查跳转表（next表）得到跳转值2，再把S2的指针移动到第二个a上，接下来比对a与a，然后。。

KMP的步骤看不明白没关系，毕竟我们还没有解释跳转表（next表）是什么，不过在这里我们只用关注结果就好了：

• BF算法中S1的指针向左移动了（回溯）
• KMP算法中S1的指针没有往回走（无回溯）

因为KMP算法不存在回溯过程，所以节省了不少时间（S1的指针只需要从头走到尾就可以了）

-------

再看看KMP算法的核心——跳转

为什么可以跳转？注意观察一下S2 = "ababc"，这个串的特点是：开头出现了ab，中间部分又出现了ab（还记得这个细节吗），详细解释一下：

如果S2末尾的c与S1的第k位匹配失败，我们可以推断出两个信息：

1. 本趟匹配失败了（c匹配失败意味着S1中的的某一部分不能匹配S2）
2. S1中第k位前的4位一定是abab（只有S2中的abab与S1中的某一部分匹配成功后才可能出现S2的c与S1第k位的比对）

如果我们忽略第2点，那么下一步是S1指针回溯，也就是BF算法将要做的；如果我们抓住第2点，再加上S2串的特点：

• 开头出现了ab，中间部分又出现了ab（再重申一遍）

就可以得到KMP算法（相当于S1中第k位之前的ab已经和S2开头的ab匹配了，所以可以直接跳转到S1的第k位与S2的第3位a比对）

好像有点明白了，那么这个跳转值2是怎么得到的？多举一些例子：

• S2 = "aba"最后一位的跳转值为0
• S2 = "abaa"最后一位的跳转值为1
• S2 = "abcabc"最后一位的跳转值为2

发现什么了吗？没错，我们求S2中第x位（此处的x是从0开始算的）的跳转值的过程是这样的：

1. 如果x = 0，那么S2[x]的跳转值为-1（首元的跳转值为-1）
2. 如果x = 1，那么S2[x]的跳转值为0（第二个元素的跳转值为0）
3. 如果S2[x - 1] = S2[0]，那么S2[x]的跳转值为1
4. 如果不满足第3条，那么跳转值为0
5. 如果S2[x - 1] = S2[0] 并且 S2[x - 2] = S2[1]，那么S2[x]的跳转值为2
6. 如果S2[x - 1] = S2[0] 并且 S2[x - 2] = S2[1] 并且 S2[x - 3] = S2[2]，那么S2[x]的跳转值为3
7. 。。。

人用眼睛按照上面的方法“目测”跳转值是最快的，但同样的过程用于计算机的话就不那么容易实现了，计算机有计算机喜欢的方式，一篇简短的博文解释了这种方式

简单的说就是——“递推”，即由已知的首项为-1，第二项为0，递推得到后面所有项，详细过程不再赘述，上面的链接博文写的非常清楚

-------

下面可以得出KMP算法的具体过程了：

1. 根据模式串S2构造跳转表（next表）
2. 从S1头开始比对，查next表得跳转值，S1指针向右移动继续比对，直至S1末尾

说白了又是在用空间换时间（next表占用的空间），当然，在此算法中next表是长度等于模式串S2长度的线性表而已，并不需要太多空间

三.实现next函数

next函数用来构造next表（跳转表），如何构造next表才是KMP算法的关键（如果不关注KMP的证明过程的话。。）

我们可以按照链接博文的方式自己实现next函数：

//参考例子：http://blog.sina.com.cn/s/blog_96ea9c6f01016l6r.html
 
#include<stdio.h>
 
void getNext(char a[], int n, int next[]){
	int i, j;
 
	next[0] = -1;//首元跳转值为-1
	next[1] = 0;//第二个元素跳转值为0
 
	for(i = 2; i < n; i++){
		j = i - 1;
 
		//递推得到next表中剩余值
		while(j != -1){
			if(a[i - 1] == a[next[j]]){
				next[i] = next[j] + 1;
				break;
			}
			else{
				j = next[j];
			}
		}
	}
}
 
main(){
	char a[] = "abaabcac";//模式串S2
	int next[8] = {0};//跳转表，初始化为全0
	int i;
 
	//构造next表
	getNext(a, 8, next);
	//输出next表
	for(i = 0; i < 8; i++){
		printf("%d ", next[i]);
	}
	printf("\n");
}

当然，上面的getNext函数好像仍然不够高效（双重循环..），但优点是易于理解。下面看看书上给的next函数：

#include<stdio.h>
 
void getNext(char a[], int n, int next[]){
	int i, j;
	i = 0;
	next[0] = -1;//首元跳转值为-1
	j = -1;
 
	//递推得到next表中剩余值
	while(i < n){
		if(j == -1 || a[i] == a[j]){
			++i;
			++j;
			next[i] = j;
		}
		else{
			j = next[j];
		}
	}
}
 
main(){
	char a[] = "abaabcac";//模式串S2
	int next[8] = {0};//跳转表，初始化为全0
	int i;
 
	//构造next表
	getNext(a, 8, next);
	//输出next表
	for(i = 0; i < 8; i++){
		printf("%d ", next[i]);
	}
	printf("\n");
}

二者的计算结果是一样的，但书上给的算法消除了双重循环，不过这样做的结果只是让代码变得更复杂了而已，没有任何实质性的优化

什么？消除了双重循环竟然没有提高效率？不可能吧？我们不妨用计数器来验证一下：

void getNext(char a[], int n, int next[]){
	int i, j;
	int counter = 0;///
 
	next[0] = -1;//首元跳转值为-1
	next[1] = 0;//第二个元素跳转值为0
 
	for(i = 2; i < n; i++){
		j = i - 1;
 
		//递推得到next表中剩余值
		while(j != -1){
			if(a[i - 1] == a[next[j]]){
				next[i] = next[j] + 1;
				counter++;///
				break;
			}
			else{
				j = next[j];
				counter++;///
			}
		}
	}
 
	printf("\n%d\n", counter);///
}
 
void getNext(char a[], int n, int next[]){
	int i, j;
	int counter = 0;///
	i = 0;
	next[0] = -1;//首元跳转值为-1
	j = -1;
 
	//递推得到next表中剩余值
	while(i < n){
		if(j == -1 || a[i] == a[j]){
			++i;
			++j;
			next[i] = j;
			counter++;///
		}
		else{
			j = next[j];
			counter++;///
		}
	}
 
	printf("\n%d\n", counter);
}

P.S.我们在具体操作的部分（最内部的if块与else块）插入了counter++;这样得到的结果才是可比的（算法进行了多少次具体操作）

运行结果如下：

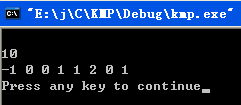
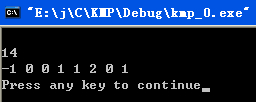
左图是我们自己实现的next函数计数结果，少的这4步是外层循环次数的差异（书上的算法是n次，我们的算法是n-2次），如果我们的算法外层循环次数也是n的话，也需要14次具体操作（我们只是做了一个简单的优化）

两个next函数只是形式不同，其内部操作顺序是完全相同的，弄清楚了next函数，KMP算法就没什么难点了（如果不关心S1的指针不用回溯的原因的话，确实只有这一个难点..）

四.KMP算法正确性的证明

（本文不在此展开，以后理解了的话可能会在此处补充缺失的内容，详细解释为什么S1的指针不用回溯，为什么之前的部分不可能再匹配。。。）

不过单纯关注“实现”的话，我们只要理解了next函数就完全可以轻松实现KMP算法了（至于为什么可以这么做，怎么证明这样做是对的。。这是数学家的事情）

五.总结

KMP算法的核心是next表的构造过程，而构造next表的关键思想就是“递推”，理解了这个，完全可以分分钟写出KMP算法。。

一点题外话：

KMP算法也有变体，本文讨论的是最原始的KMP算法，常见的变体有：

• next表首元为0（而不是-1），最终得到的结果就是给我们的next表中每个元素都+1，只是约定不同而已（从0开始与从1开始），并没有实质性的差别
• next表中有多个-1（我们的结果中有且只有一个-1，也就是next表首元），这是一种实质性的优化，能有效的提高效率。其实也就是在构造next表的时候比我们多做了一步，构造过程变复杂了一点点，但匹配算法的比对次数减少了