Kolakoski

Kolakoski序列：我们知道的还是太少

上帝创造了整数，其余的则是我们人类的事了。正因为如此，质数、完全数、Fibonacci 数之类的数列才会让数学家们如痴如醉，因为它们的存在是如此自然，没有任何人造的因素。事实上，数学家们对这些数的认识也越来越丰富，挖掘出了这些数列中越来越深刻的性质。

不过，人类确实太渺小了。还有好多构造异常简单的“纯天然数列”，我们了解得实在太少。Kolakoski 数列就是最好的例子之一。

Kolakoski 数列仅由 1 和 2 构成，其中头 100 个数是

1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1,
2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1,
1, 2, 1, 2, 2, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2,
1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 1, 1, 2,
2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 1, 1, 2, 2, …

如果我们把连续的相同数看作一组的话，整个数列的定义就只有两句话： a(1) = 1 ， a(n) 表示第 n 组数的长度。例如，a(6) = 2，就表明第 6 组数（从第 8 个数算起）的长度就是 2。注意，有了这几个条件，整个序列就已经唯一地确定了！a(1) = 1 就表明第一组数只有一个数，因此下一个数必须要换成 2 ，因此 a(2) = 2 ；而 a(2) = 2 又说明这个 2 必须要连着出现两个，因此 a(3) = 2；而 a(3) = 2 就表明数列接下来要有两个 1 ，等等。也就是说，生成这个数列的“参数”就是这个数列本身。更酷的说法则是，这个数列是分形的：如果把每一组数用它的长度来替换，就会得到这个数列本身。另外一个可能有些出人意料的事实是：Kolakoski 数列在 OEIS 中的序号非常靠前—— A000002。

关于 Kolakoski 数列，我们知道些什么？很少。我们知道，这个数列可以用递归式 a(a(1) + a(2) + … + a(k)) = (3 + (-1)k)/2 来表达。我们目前已经知道，去掉数列最前面的 1，剩下的部分可以从 22 开始，由替换规则 22→2211，21→221，12→211，11→21 迭代产生。

Kolakoski 数列的第 n 项有非递归的公式吗？目前我们还不知道。已经出现过的数字串今后都还会再次出现吗？目前我们也不知道。还有，我们有理由猜想，数列中 1 和 2 的个数各占一半。下图显示的就是数列前 n 项中数字 1 所占的比例，可见我们的猜想很可能是对的。

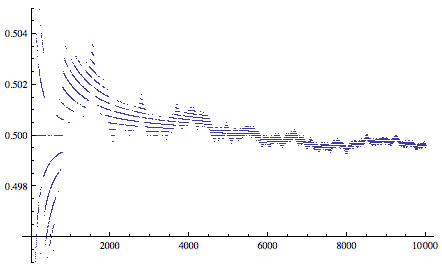
不过，目前还没有人能够证明这一点。而最近的一些研究则表明，数字 1 的比例很可能不是 1/2 。当然，还有第三种可能——这个极限可能根本不存在。这无疑又是一个最折磨人的数学未解之谜。