Eigen学习

　　Eigen 是一个基于C++的线性代数库，其中实现大量常用的线性代数算法，包括常规矩阵计算，矩阵变换，矩阵分解，矩阵块操作。Eigen 广泛地应用在开源项目中，例如OpenCV，PCL(Point Cloud Library)，ROS等。其实Eigen中算法都可以在matlab中找到，但是由于matlab是半开源的。所以，如果想在自己的项目中使用，还是要义无反顾地选择Eigen。Eigen目前的版本是3.3.4(2018.4.21)。

　　来看Eigen官网的第一个例子：

　　

 #include <iostream>
 #include <eigen3/Eigen/Dense>

 using Eigen::MatrixXd;

 int main(int argc ,char** argv)
 {
     MatrixXd:: m(,);
     m(,) = ;
     m(,) = 2.5;
     m(,) = -;
     m(,) = m(,) + m(,);
     std::cout<<m<<std::endl;
     return ;
 }

首先，代码引入了eigen的头文件，这里Eigen/Dense 一次引入了多个常用的模块。

　　程序首先定义了一个2 x 2的矩阵。根据Eigen的定义 ，MatrixXd，这个类型可以拆成三部分来看，Matrix-X-d，Matrix表示定义的是一个矩阵，X表示定义的矩阵维度不确定，d表示double，指矩阵中每一个元素都是double类型的。m(2,2)指定了矩阵的大小是2x2的。从第9 行到第12 行则为矩阵中的元素进行了赋值操作。

　　最后输出矩阵。

　　在系统中运行输出如下：

　　

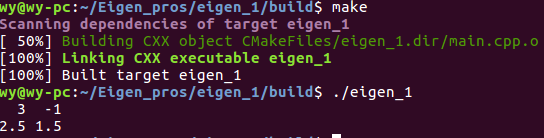
来看第二个例子，区分一下矩阵（Matrix）和向量(Vector)的区别：

 #include <iostream>
 #include <eigen3/Eigen/Dense>

 using namespace Eigen;
 uisng namespace std;

 int main(int argc ,char** argv)
 {
　　　　// 创建一个3 x 3的随机矩阵，每个元素的范围都在（-1,1）之间
     MatrixXd m  = MatrixXd::Random(,);
　　　　// 将每个元素的范围设置在 （10,110）之间，MatrixXd::Cosntant() 用于产生每个元素都相同的矩阵，这里每个元素都是1.2
     m = (m + MatrixXd::Constant(,,1.2)) * ;
     cout<<"m="<<endl<<m<<endl;
　　　　//创建一个长度为 3 的向量，
     VectorXd v();
　　　　//为向量元素赋值，这里Eigen 将 << 操作符重载了。
     v<<,,3;
　　　　//矩阵和向量做乘法并输出结果
     cout<<"m*v"<<m*v<<endl;

     return ;
 }

运行结果如下：

　　　　

　上面的例子展示生成矩阵和向量的不同方法，其实向量就是列数为1 的矩阵。