牛可乐发红包脱单OI赛 C 小可爱表白

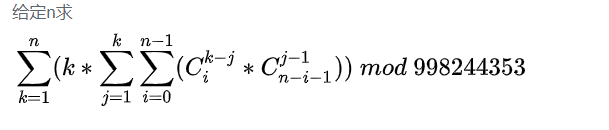
打个暴力查一下OEIS，5min做完

出题人一开始把式子打错了，一开始的式子的结果为$n * (n + 3) * 2^{n - 3}$

我们考虑化式子

首先考虑

$\sum\limits_{j = 1}^k \sum\limits_{i = 0}^{n - 1} \binom{i}{k- j} * \binom{n - i - 1}{j - 1}$

$= \sum\limits_{i = 0}^{n - 1} \sum\limits_{j = 1}^k \binom{i}{k- j} * \binom{n - i - 1}{j - 1}$

$=  \sum\limits_{i = 0}^{n - 1} \sum\limits_{j = 0}^{k - 1} \binom{i}{k- j - 1} * \binom{n - i - 1}{j}$

我们考虑对后面运用范德蒙德卷积公式$\sum\limits_{i = 0}^k \binom{n}{i} \binom{m}{k - i} = \binom{n + m}{k}$，可以得到

$= \sum\limits_{i = 0}^{n - 1} \binom{n - 1}{k - 1}$

$= n * \binom{n - 1}{k - 1}$

$= k \binom{n}{k}$

因此，原式等于$\sum\limits_{k = 1}^n k^2 \binom{n}{k}$

我们可以对$(1 + x)^n = \sum\limits_{i = 0}^n \binom{n}{i} x^i$连续求导$2$次得到下面的恒等式

$\sum\limits_{k = 1}^n k^2 \binom{n}{k} = n * (n + 1) * 2^{n - 2}$

代码实现....算了吧...

复杂度$O(\log n)$