DP Training(Updating)

感觉前面做了那么多$dp$全是自己想的还是太少啊……

好像在LZT的博客上看到了不错的资源？赶紧开坑，以一句话题解为主

Codeforces 419B

第一题就开始盗图

由于只有一个交点，手玩一下发现两人的路径可以分为四块区域，且只有两种情况：

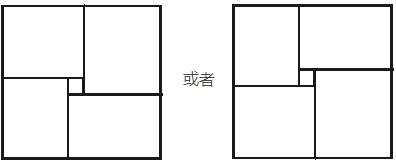
预处理四个方向的最长距离，枚举相交点即可

FZU 2234:

将往返路径看成从起点出发的两条路径

$dp[Xa][Xb][STEP]$用三维记录两个当前位置，转移时注意两点是否重复

Tip：建状态时注意是否有能合并的维度！

POJ 1050：

一开始想成最大全1子矩阵了……

这样权值和最大子矩阵好像也只能$O(n^3)$做：

$O(n^2)$枚举左右端点，再转换成1维$O(n)$算一遍从上到下的最长子序列

HDU 1024：

最大$m$字段和我可能之前学的是假的转移……

直接设$dp[i][j]$表示取前$i$个且第$i$个必选的最大$j$字段和，不需要再加一维表示是否选$i$

转移：$dp[i][j]=max(dp[i-1][j],dp[k][j-1])+a[i]$，滚动数组+记录前一层到$i-1$的最大值

Tip：

1、分清哪一层滚动来确定嵌套顺序

2、第二层(i)不能每次从1开始枚举，要从$j$开始！！！

边界尽量卡死防止出错

加强版见：https://www.cnblogs.com/newera/p/9534648.html

HDU 1257：

可以直接贪心判断是否需要增加系统并维护每个系统的末尾值

不过这其实是一道$Dilworth$定理相关的题

借此机会又好好复习了下集合论里的一些概念和证明：传送门

这题将偏序关系设为$i<j$且$a[i]<a[j]$，那么每个系统就是一条反链

最长链长度=最小反链覆盖，因此直接求LIS即可

HDU 1025：

按一边排序后直接LIS，注意输出里的$road$和$roads$……（还是要好好看样例！）

HDU 5282:

这里用$cnt[i][j]$计数时按是否选$a_i$分类：

（注意分类转移的设置！）

1、不选$a_i$：$f[i][j]=f[i-1][j]$时加上$cnt[i-1][j]$

2、选$a_i$：预处理出$b_j$前第一个与$a_i$相同的位置$pre$

$f[i-1][pre-1]+1=f[i][j]$时加上$cnt[i-1][pre-1]$

FZU 2214:

尽量用范围小的量做状态！

POJ 2184:

要求在两个量和都大于0的情况下求最大的和

这样必定不能用和来建状态，而应该以其中一个量作状态用值存另一个量的最大值

UVa 624：

可以把$weight,value$都看成$w[i]$直接做背包

也可以用$vis[i][j]$表示能否凑出$j$

HDU 2639：

求第$K$大背包

转移的项与原来相同，只是对于每个原来状态都记录下前$K$大的值

每次转移时将$2*K$个数$O(n)$合并求出前$K$大即可

HDU 5534：

只要$\sum d_i=2*(n-1)$，那么就存在这样的一棵树

如果将每个点作为第一维那么转移是$O(n)$的，思考如何优化

发现将$d_i$相同的点合并看成一种物品再进行一些处理就能跑完全背包了！

Tips:

1、为了消除物品总数必须为$n$的限制，先给每个点分配1的度数，只考虑增量

这样就变成$W=n-2,num=n-2,w[i]'=w[i]-w[1]$的无限制完全背包了

2、注意这里要求总重量恰为$n-2$，而非至多，因此要把$dp$数组初始化为-INF$