[2009国家集训队]小Z的袜子(hose) 浅谈莫队

浅谈莫队

推荐学习博客 http://foreseeable97.logdown.com/posts/158522-233333

借用题目： bzoj 2038 2009 国家集训队 小Z的袜子http://www.lydsy.com/JudgeOnline/problem.php?id=2038

[2009国家集训队]小Z的袜子(hose)

http://www.lydsy.com/JudgeOnline/problem.php?id=2038

Time Limit:  Sec  Memory Limit:  MB

Description

作为一个生活散漫的人，小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天，小Z再也无法忍受这恼人的找袜子过程，于是他决定听天由命……
具体来说，小Z把这N只袜子从1到N编号，然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双，甚至不在意两只袜子是否一左一右，他却很在意袜子的颜色，毕竟穿两只不同色的袜子会很尴尬。
你的任务便是告诉小Z，他有多大的概率抽到两只颜色相同的袜子。当然，小Z希望这个概率尽量高，所以他可能会询问多个(L,R)以方便自己选择。

Input

输入文件第一行包含两个正整数N和M。N为袜子的数量，M为小Z所提的询问的数量。接下来一行包含N个正整数Ci，其中Ci表示第i只袜子的颜色，相同的颜色用相同的数字表示。再接下来M行，每行两个正整数L，R表示一个询问。

Output

包含M行，对于每个询问在一行中输出分数A/B表示从该询问的区间[L,R]中随机抽出两只袜子颜色相同的概率。若该概率为0则输出0/，否则输出的A/B必须为最简分数。（详见样例）

Sample Input

Sample Output

/
/
/
/
【样例解释】
询问1：共C(,)=10种可能，其中抽出两个2有1种可能，抽出两个3有3种可能，概率为(+)/=/=/。
询问2：共C(,)=3种可能，无法抽到颜色相同的袜子，概率为0/=/。
询问3：共C(,)=3种可能，均为抽出两个3，概率为3/=/。
注：上述C(a, b)表示组合数，组合数C(a, b)等价于在a个不同的物品中选取b个的选取方案数。
【数据规模和约定】
%的数据中 N,M ≤ ；
%的数据中 N,M ≤ ；
%的数据中 N,M ≤ ， ≤ L < R ≤ N，Ci ≤ N。

题目简介

莫队算法

 

本方法由莫涛提出，故尊称为莫队算法

 

使用前提：

1、离线操作

2、若已知[l,r]内的答案，可以在O（1）时间内得到[l-1,r],[l+1,r],[l,r-1],[l,r+1]的答案，即可使用莫队算法，时间复杂度O（n^1.5）。

   若可在O(logn)内移动区间，时间复杂度则为O（n^1.5*logn）

 

个人理解：

莫队算法本质是分块

通过左右指针的移动避免了重复状态的计算

 

就本题来说

，

sum表示区间内数i的出现次数

那么∑sum[i]=r-l+1 

           2*（r-l+1）!

分母=  -----------   = （r-l）*（r-l+1）

         2!*(r-l-1) !

可以O（1）解决

那么就差∑sum[i]²

本题满足离线操作，如果我们能证明∑sum[i]²可以O（1）或O（logn）求出来，就可以使用莫队算法

由此图可以看出，满足前提条件2

所以我们可以使用莫队算法

还有，如果先询问[1,n]，再问[1,1]，再问[n,n]，时间复杂度不还是n²吗

所以，为了避免指针在整个序列中移动，我们需要分块

 

因为分块保证了莫队算法的时间复杂度

 

如何分块？

令块的大小为根号n

先根据询问区间左端点所在块，从小到大排，这样就将整个操作序列划分为了根号n块

对于每个块内的询问，根据右端点从小到大排

然后我们从左到右顺序计算每个询问的答案

这样可以保证时间复杂度为O（n^1.5）

 

时间复杂度分析：

A.左端点

  1.块内的，由于块的大小为根号n，所以同一块内左端点一次询问最多移动根号n，即n^0.5次，m次询问总移动O（n*n^0.5）=O(n^1.5)

  2、不在同一块内的，以为块的大小为n^0.5，所以跨越一次最多加上O（n^0.5），最多能跨越(n^0.5)次，所以跨越块导致左端点最多加上O（n）

 所以左端点总的移动次数为O（n^1.5）+O(n)

B.右端点

 1、块内的，右端点最多从1移动到n，有根号n个块，所以右端点最多移动O（n^1.5）次

 2、跨越块的，最多跨越个根号n次，每次跨越最多移动n次，所以右端点最多移动 O（n^1.5）

所以右端点总移动次数为O（n^1.5）+O(n^1.5)

所以时间复杂度为O（n^1.5）

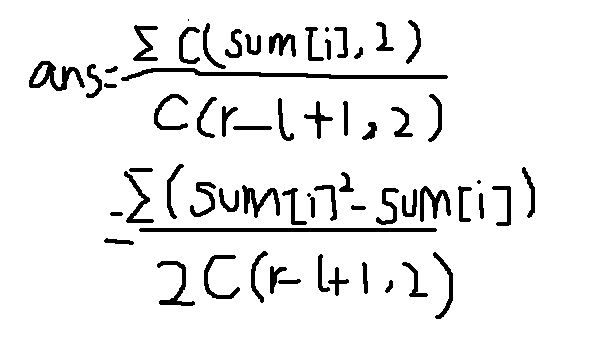
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
int col[];
struct node
{
    int l,r,id,pos;
    long long a,b;
}e[];
int n,m,S;
long long h,ans,sum[];
bool cmp(node p,node q)
{
    if(p.pos!=q.pos) return p.pos<q.pos;
    return p.r<q.r;
}
bool id(node p,node q)
{
    return p.id<q.id;
}
void update(int x,int k)
{
    ans-=sum[col[x]]*sum[col[x]];
    sum[col[x]]+=k;
    ans+=sum[col[x]]*sum[col[x]];
}
long long gcd(long long a,long long b)
{
    return b== ? a:gcd(b,a%b);
}
void solve()
{
    int l=,r=;
    for(int i=;i<=m;i++)
    {
        while(l<e[i].l) update(l++,-);
        while(l>e[i].l) update(--l,);
        while(r<e[i].r) update(++r,);
        while(r>e[i].r) update(r--,-);
        e[i].a=ans-(r-l+);
        e[i].b=1ll*(r-l)*(r-l+);
        h=gcd(e[i].a,e[i].b);
        e[i].a/=h;e[i].b/=h;
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    S=sqrt(n);
    for(int i=;i<=n;i++) scanf("%d",&col[i]);
    for(int i=;i<=m;i++)
     {
        scanf("%d%d",&e[i].l,&e[i].r);
        e[i].id=i;
        e[i].pos=(e[i].l-)/S+;
    }
    sort(e+,e+m+,cmp);
    solve();
    sort(e+,e+m+,id);
    for(int i=;i<=m;i++) printf("%lld/%lld\n",e[i].a,e[i].b);
}

小细节：l最初从1开始，r从0开始

因为l最开始一定小于e[i].l,这种情况下先计算l，在自加

r最开始一定小于e[i].r,这种情况下先自加，再计算