【Cf #503 B】The hat（二分）

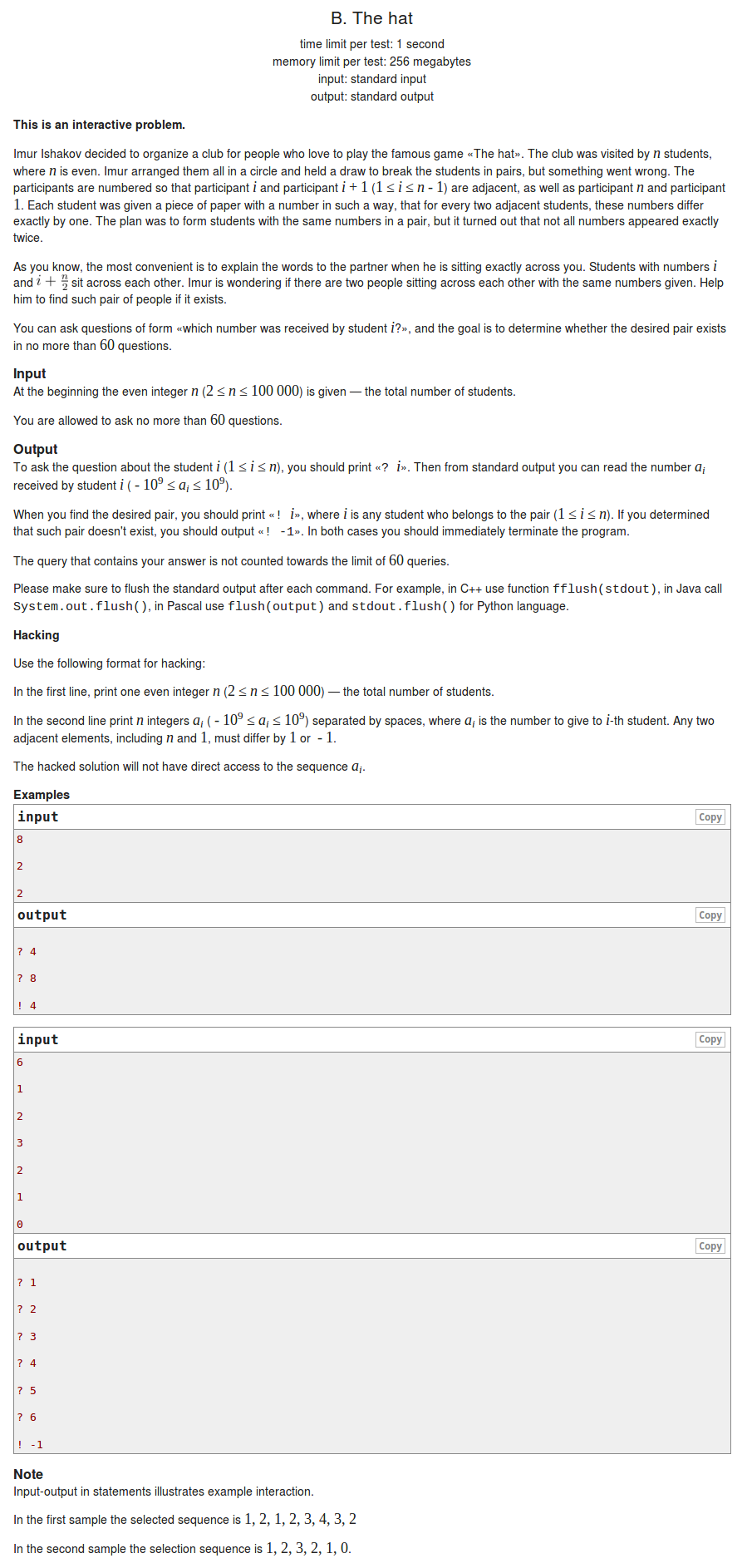
为什么Cf上所有的交互题都是$binary \; Search$。。。

把序列分成前后两个相等的部分，每一个都可以看成一条斜率为正负$1$的折线。我们把他们放在一起，显然，当折线的交点的横坐标为整数时有解。

我们考虑序列元素$a_{i}, a_{i + \frac{n}{2}}$，他们的差的奇偶性对于每一个$i$都是一样的，因为随着横坐标的增加，纵坐标之差要么不变，要么加减$2$。

显然如果我们询问$a_{1}, a_{1 + \frac{n}{2}}$的差是奇数，那就不可能存在解了。

我们把折线的左右边界设成重合，也就是第一条折线的右边界的点就是第二条折线左边界的点。不考虑边界处相交时，显然两条折线是交错的，于是必定有交点。

我们只要求出任意一组解就可以了，于是可以二分，可以快速判断左右区间中哪一个一定存在解，根据交错必定有解就可以了。

$\bigodot$技巧&套路：

• 根据奇偶性可以证明将问题简化

#include <cstdio>
#include <cstdlib>
#include <iostream>
using namespace std;

const int N = ;

int n, a[N];

int Ask(int p) {
  cout << "? " << p << endl;
  cin >> a[p];
  cout << "? " << p + n /  << endl;
  cin >> a[p + n / ];
  if (a[p] == a[p + n / ]) {
    cout << "! " << p << endl;
    exit();
  }
  return a[p] < a[p + n / ];
}

int main() {
  scanf("%d", &n);
  int type = Ask();
  if ((a[] - a[ + n / ]) & ) {
    cout << "! -1" << endl;
    return ;
  }
  int nl = , nr = n / ;
  for (int md; nl <= nr; ) {
    md = (nl + nr) >> ;
    if (Ask(md) == type) {
      nl = md + ;
    } else {
      nr = md - ;
    }
  }

  return ;
}