poj3070 Fibonacci（矩阵快速幂）

矩阵快速幂基本应用。

对于矩阵乘法与递推式之间的关系：

如：在斐波那契数列之中

f[i] = 1*f[i-1]+1*f[i-2]  f[i-1] = 1*f[i-1] + 0*f[i-2]。即

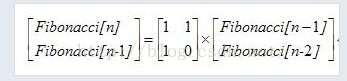
所以，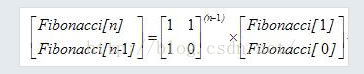

就这两幅图完美诠释了斐波那契数列如何用矩阵来实现。

 #include<iostream>
 #include<cstring>
 using namespace std;
 typedef long long ll;
 const int Mod=;
 struct mat{
     ll a[][];
 };
 mat mat_mul(mat x,mat y){
     mat ans;
     memset(ans.a,,sizeof(ans.a));
     for (int i=;i<;i++){
         for (int j=;j<;j++)
         for (int k=;k<;k++)
             ans.a[i][j]=ans.a[i][j]+(x.a[i][k]*y.a[k][j])%Mod;
     }
     return ans;
 }
 ll mat_pow(ll n){
     mat c,res;
     c.a[][]=c.a[][]=c.a[][]=;
     c.a[][]=;
     memset(res.a,,sizeof(res.a));
     for (int i=;i<;i++) res.a[i][i]=;
     while (n){
         if (n&) res=mat_mul(res,c);
         c=mat_mul(c,c);
         n>>=;
     }
     return res.a[][]%Mod;
 }
 int main(){
     ll n;
     while (cin >> n && n!=-){
         cout << mat_pow(n) << endl;
     }
     return ;
 }