【LeetCode题解】169_求众数（Majority-Element）

169_求众数（Majority-Element）

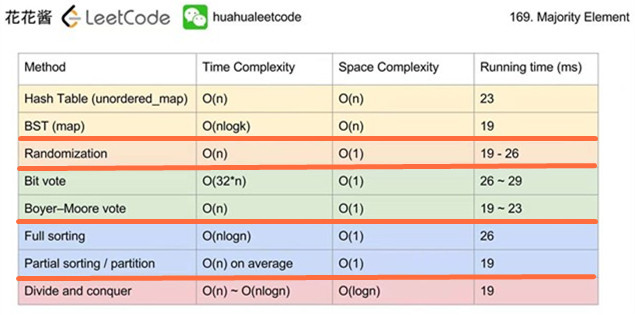
这道题有 5 种方法，8 种实现，详细分析可以看花花酱的 YouTube 专栏。

目录

• 169_求众数（Majority-Element）
  • 描述
    • 解法一：暴力法
    • 思路
    • Java 实现
    • Python 实现
    • 复杂度分析
  • 解法二：哈希表
    • 思路
    • Java 实现
    • Python 实现
    • 复杂度分析
  • 解法三：排序
    • Java 实现
    • Python 实现
    • 复杂度分析
  • 解法四：随机选择【待完成】
    • 思路
    • Java实现
    • Python 实现
    • 复杂度分析
  • 解法五：分而治之（Divide and conquer）【待完成】
    • 思路
    • Java 实现
    • Python 实现
    • 复杂度分析
  • 解法六：多数投票算法（Boyer-Moore majority vote algorithm）
    • 思路
    • Java 实现
    • Python 实现
    • 复杂度分析

描述

给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在众数。

示例 1:

输入: [3,2,3]
输出: 3

示例 2:

输入: [2,2,1,1,1,2,2]
输出: 2

解法一：暴力法

思路

遍历数组中的每个元素，统计该元素出现的次数（嵌套遍历），如果该元素出现的次数 \(> \left \lfloor n/2 \right \rfloor\)，则该元素就是数组的众数。

Java 实现

class Solution {
    public int majorityElement(int[] nums) {
        int majorityCount = nums.length / 2;
        for (int num1 : nums) {
            int count = 0;
            for (int num2 : nums) {
                if (num2 == num1) {
                    ++count;
                }
            }
            if (count > majorityCount) {
                return num1;
            }
        }
        throw new IllegalArgumentException("The array does not contain a majority element!");
    }
}

Python 实现

class Solution:
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        majority_count = len(nums) // 2
        for num1 in nums:
            count = sum(1 for num2 in nums if num2 == num1)
            if count > majority_count:
                return num1

复杂度分析

• 时间复杂度：\(O(n^2)\)，其中 \(n\) 表示数组的长度，由于嵌套了两层 for 循环，因此总的时间复杂度是 \(O(n^2)\) 的
• 空间复杂度：\(O(1)\)

解法二：哈希表

思路

利用哈希表记录数组中元素出现的次数，由于哈希表的插入操作的时间复杂度是 \(O(1)\) 的，所以遍历整个数组统计出现次数的操作的时间复杂度是 \(O(n)\) 的。接着，再遍历一遍哈希表，取出众数。

Java 实现

class Solution {
    public int majorityElement(int[] nums) {
        Map<Integer, Integer> counts = new HashMap<>();
        for (int num : nums) {
            if (counts.containsKey(num)) {
                counts.replace(num, counts.get(num) + 1);
            } else {
                counts.put(num, 1);
            }
        }

        Map.Entry<Integer, Integer> majorityEntry = null;
        for (Map.Entry<Integer, Integer> entry : counts.entrySet()) {
            if (majorityEntry == null || entry.getValue() > majorityEntry.getValue()) {
                majorityEntry = entry;
            }
        }

        return majorityEntry.getKey();
    }
}

Python 实现

class Solution:
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        counts = dict()
        for num in nums:
            counts[num] = counts.get(num, 0) + 1
		return max(counts, key=counts.get)

复杂度分析

• 时间复杂度：\(O(n)\)，其中 \(n\) 为数组的长度。由于哈希表中元素的数目最多为 \(n - \left( \left \lfloor n/2 \right \rfloor + 1 \right) + 1 = n - \left \lfloor n/2 \right \rfloor\)，因此遍历一次哈希表最多需要 \(n - \left \lfloor n/2 \right \rfloor\) 次操作，而遍历一遍数组需要 \(n\) 次操作，所以总的时间复杂度是 \(O(n)\) 的
• 空间复杂度：\(O(n)\)，因为哈希表最多需要保存 \(n - \left \lfloor n/2 \right \rfloor\) 个元素

解法三：排序

将数组按照顺序（递增或者递减）排列好后，索引为 \(\left \lfloor n/2 \right \rfloor\) 的元素就是数组的众数。

Java 实现

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length / 2];
    }
}

Python 实现

class Solution:
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        return sorted(nums)[len(nums) // 2]

复杂度分析

• 时间复杂度：\(O(n \log(n))\)，其中 \(n\) 表示数组的长度，对数组进行排序的时间复杂度为 \(O(n \log(n))\) 的
• 空间复杂度：\(O(n)\) 或者 \(O(1)\)，取决于是否可以直接对原数组直接进行排序，如果不允许的话，需要额外的空间复制数组

解法四：随机选择【待完成】

思路

Java实现

Python 实现

复杂度分析

解法五：分而治之（Divide and conquer）【待完成】

思路

Java 实现

Python 实现

复杂度分析

解法六：多数投票算法（Boyer-Moore majority vote algorithm）

思路

多数投票算法一般用于寻找一个序列的多数元素（只需要线性时间和常数空间），是一种典型的流式算法（streaming algorithm）。但是，一般来说，该算法无法找到一个序列的众数（mode），除非众数出现的次数大于 \(\lfloor n/2 \rfloor\) 次。多数投票算法的思想是这样：统计一个序列中的所有元素，将多数元素记为 \(+1\)，其余的元素记为 \(-1\)，那么最后的和一定是正的。具体地，该算法会维护两个变量，一个用于记录序列中的元素，记为 m，一个作为计数器，记为 count。遍历数组中的每个元素，如果当前的 count 为 0，则将当前元素保存在 m 中，并设 count 为1；如果 count 不为0，则判断当前元素与 m 是否相等，相等则 count 加一，不等则 count 减一。遍历结束，变量 m 就是我们寻找的多数元素。

Java 实现

class Solution {
    public int majorityElement(int[] nums) {
        int me = nums[0], count = 1;
        for (int i = 1; i < nums.length; ++i) {
            if (count == 0) {
                me = nums[i];
                count = 1;
            } else if (me == nums[i]) {
                ++count;
            } else {
                --count;
            }
        }
        return me;
    }
}

Python 实现

class Solution:
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        me, count = 0, 0
        for num in nums:
            if count == 0:
                me, count = num, 1
            elif me == num:
                count += 1
            else:
                count -= 1
        return me

复杂度分析

• 时间复杂度：\(O(n)\)，其中 \(n\) 表示数组的长度
• 空间复杂度：\(O(1)\)