P2607 [ZJOI2008]骑士

题目描述

Z国的骑士团是一个很有势力的组织，帮会中汇聚了来自各地的精英。他们劫富济贫，惩恶扬善，受到社会各界的赞扬。

最近发生了一件可怕的事情，邪恶的Y国发动了一场针对Z国的侵略战争。战火绵延五百里，在和平环境中安逸了数百年的Z国又怎能抵挡的住Y国的军队。于是人们把所有的希望都寄托在了骑士团的身上，就像期待有一个真龙天子的降生，带领正义打败邪恶。

骑士团是肯定具有打败邪恶势力的能力的，但是骑士们互相之间往往有一些矛盾。每个骑士都有且仅有一个自己最厌恶的骑士（当然不是他自己），他是绝对不会与自己最厌恶的人一同出征的。

战火绵延，人民生灵涂炭，组织起一个骑士军团加入战斗刻不容缓！国王交给了你一个艰巨的任务，从所有的骑士中选出一个骑士军团，使得军团内没有矛盾的两人（不存在一个骑士与他最痛恨的人一同被选入骑士军团的情况），并且，使得这支骑士军团最具有战斗力。

为了描述战斗力，我们将骑士按照1至N编号，给每名骑士一个战斗力的估计，一个军团的战斗力为所有骑士的战斗力总和。

输入输出格式

输入格式：

输入文件knight.in第一行包含一个正整数N，描述骑士团的人数。

接下来N行，每行两个正整数，按顺序描述每一名骑士的战斗力和他最痛恨的骑士。

输出格式：

输出文件knight.out应包含一行，包含一个整数，表示你所选出的骑士军团的战斗力。

输入输出样例

输入样例#1：
复制

3
10 2
20 3
30 1

输出样例#1： 复制

30

说明

对于30%的测试数据，满足N ≤ 10；

对于60%的测试数据，满足N ≤ 100；

对于80%的测试数据，满足N ≤ 10 000。

对于100%的测试数据，满足N ≤ 1 000 000，每名骑士的战斗力都是不大于 1 000 000的正整数。

---

建图后大概形状就是一些树然后每棵树的树顶有一条指向其子树的边。

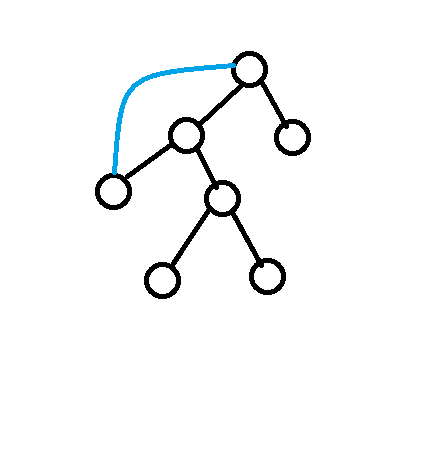
我们会发现一旦把这条边去掉后就变成了一棵普通的树最大独立集问题。dp f[i][(1或0）]表示第i个节点选或不选时其子树的能够产生最大战斗力

所以dp再加一维表示选树根还是不选选树根的情况。当然在不选树根时其指向点也不是必选，可能出现都不选总战斗力最大的情况

于是重新变回基础树形dp

---

#include<iostream>
#include<stdio.h>
#include<cstring>

using namespace std;

int q,h,i,m,n,j,k,head[1000001],s[1000001],a[1000001],ver[1000001],cnt,nex[1000001];
bool bl[1000001],b[1000001];
long long w,e,f[1000001][2];

void add(int x,int y)
{
    cnt+=1;
    ver[cnt]=y;
    nex[cnt]=head[x];
    head[x]=cnt;
}

int ch(int k)
{
    b[k]=1;
    if(b[s[k]]) return k;
    return ch(s[k]);
}

void dfs(int k,bool u)
{
    b[k]=1;
    for(int i=head[k];i;i=nex[i]) if(ver[i]!=q) dfs(ver[i],u);
    f[k][1]=a[k];
    if((k==s[q])&&u)f[k][1]=0;
    if((k==q)&& !u) f[k][1]=0;
    for(int i=head[k];i;i=nex[i])
    {
        int t=ver[i];
        if(t==q)continue;
        if((k==s[q])&&(u))
        {
            f[k][0]+=max(f[t][1],f[t][0]);
            f[k][1]+=max(f[t][0],f[t][1]);
        }
        else
        {
            f[k][0]+=max(f[t][1],f[t][0]);
            f[k][1]+=f[t][0];
        }
    }
}

int main()
{
    scanf("%d",&n);
    for(i=1;i<=n;i++)
    {
        scanf("%d%d",&a[i],&s[i]);
        add(s[i],i);
    }
    for(i=1;i<=n;i++)
    {
        w=0;
        if(!b[i])
        {
            memset(f,0,sizeof(f));
            q=ch(i);
            dfs(q,1);
            w=max(f[q][1],f[q][0]);
            memset(f,0,sizeof(f));
            dfs(q,0);
            w=max(w,f[q][0]);
            e+=w;
        }
    }
    cout<<e;
}