Fuzzy模糊推导(Matlab实现)

问题呈述

在模糊控制这门课程中，学到了与模糊数学及模糊推理相关的内容，但是并不太清楚我们在选择模糊规则时应该如何处理，是所有的规则都需要由人手工选择，还是仅需要选择其中的一部分就可以了。因此，在课程示例的基础上做了如下的探究。

设计一个以E、EC作为输入，U作为输出的模糊推理系统，令E、EC、U的隶属度函数为如下：

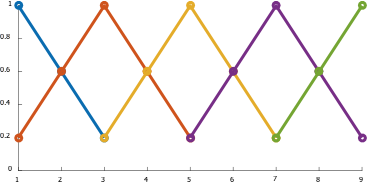
1	0.6	0.2	0	0	0	0	0	0
0.2	0.6	1	0.6	0.2	0	0	0	0
0	0	0.2	0.6	1	0.6	0.2	0	0
0	0	0	0	0.2	0.6	1	0.6	0.2
0	0	0	0	0	0	0.2	0.6	1

分别给定“中心十字规则”以及“最强对角线规则”作为初始规则，观察由此推导出的结果，以验证初始模糊规则库应该如何选择。

结果

中心十字规则

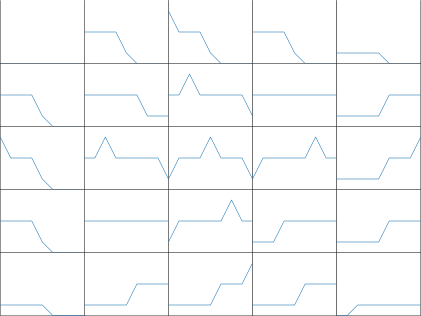
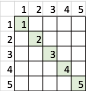
其中，列索引代表E，行索引代表EC，中间的数据区域代表U。1代表负大(NB)，2代表负中(NM)，3代表零(Z)，4代表正中(PB)，5代表正大(PB)。

最强对角线

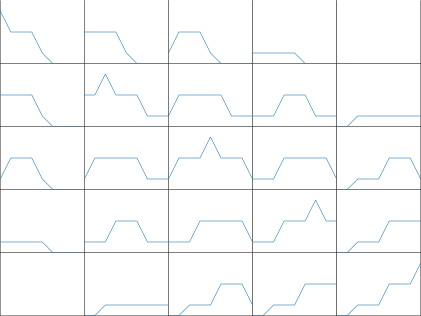
结果分析

从上面的结果可以分析得出：

1. 当提供部分规则时，其它规则可由这些规则导出；
2. 强对角线规则作为初始规则时，推导效果较好；
3. 在强对角线中，左下角和右上角的隶属度为零，这与人的主观判断相同，即“误差正大，但是误差速度为负大，即误差减小（趋于零）的速度最大”，此时不应有主观判断，即维持原态即可。

Additional

tight_subplot.m

function ha = tight_subplot(Nh, Nw, gap, marg_h, marg_w)

% tight_subplot creates "subplot" axes with adjustable gaps and margins
%
% ha = tight_subplot(Nh, Nw, gap, marg_h, marg_w)
%
%   in:  Nh      number of axes in hight (vertical direction)
%        Nw      number of axes in width (horizontaldirection)
%        gap     gaps between the axes in normalized units (0...1)
%                   or [gap_h gap_w] for different gaps in height and width
%        marg_h  margins in height in normalized units (0...1)
%                   or [lower upper] for different lower and upper margins
%        marg_w  margins in width in normalized units (0...1)
%                   or [left right] for different left and right margins
%
%  out:  ha     array of handles of the axes objects
%                   starting from upper left corner, going row-wise as in
%                   going row-wise as in
%
%  Example: ha = tight_subplot(3,2,[.01 .03],[.1 .01],[.01 .01])
%           for ii = 1:6; axes(ha(ii)); plot(randn(10,ii)); end
%           set(ha(1:4),'XTickLabel',''); set(ha,'YTickLabel','')

% Pekka Kumpulainen 20.6.2010   @tut.fi
% Tampere University of Technology / Automation Science and Engineering

if nargin<3; gap = .02; end
if nargin<4 || isempty(marg_h); marg_h = .05; end
if nargin<5; marg_w = .05; end

if numel(gap)==1;
    gap = [gap gap];
end
if numel(marg_w)==1;
    marg_w = [marg_w marg_w];
end
if numel(marg_h)==1;
    marg_h = [marg_h marg_h];
end

axh = (1-sum(marg_h)-(Nh-1)*gap(1))/Nh;
axw = (1-sum(marg_w)-(Nw-1)*gap(2))/Nw;

py = 1-marg_h(2)-axh; 

ha = zeros(Nh*Nw,1);
ii = 0;
for ih = 1:Nh
    px = marg_w(1);

    for ix = 1:Nw
        ii = ii+1;
        ha(ii) = axes('Units','normalized', ...
            'Position',[px py axw axh], ...
            'XTickLabel','', ...
            'YTickLabel','');
        px = px+axw+gap(2);
    end
    py = py-axh-gap(1);
end

中心十字规则

clc;
E = [1,0.6,0,0,0,0,0,0,0;0.2,0.6,1,0.6,0.2,0,0,0,0;0,0,0.2,0.6,1,0.6,0.2,0,0;0,0,0,0,0.2,0.6,1,0.6,0.2;0,0,0,0,0,0,0.2,0.6,1];
EC = E;
U = E;

% ----------------------------------------------------------------------------------
% Calculate R
% Deduct relationship
% ----------------------------------------------------------------------------------
R = zeros(81,9);
for i = 1:5
	A = E(i,:)';
	B = EC(3,:);
	C = U(i,:);
	AB = min(repmat(A,1,9), repmat(B,9,1));
	AB = reshape(AB, [81,1]);
	RC = min(repmat(AB,1,9), repmat(C, 81,1));
	R = max(R,RC);
end

for i = [1,2,4,5]
	A = E(3,:)';
	B = EC(i,:);
	C = U(i,:);
	AB = min(repmat(A,1,9), repmat(B,9,1));
	AB = reshape(AB, [81,1]);
	RC = min(repmat(AB,1,9), repmat(C, 81,1));
	R = max(R,RC);
end

% ----------------------------------------------------------------------------------
% Calculate C
% Relationship induction
% ----------------------------------------------------------------------------------

C = zeros(9,5,5);
for i = 1:5
	for j = 1:5
		A = E(i,:)';
		B = EC(j,:);
		AB = min(repmat(A,1,9), repmat(B,9,1));
		AB = reshape(AB, [81,1]);
		C(:,i,j) = max(min(repmat(AB, 1, 9), R));
	end
end

% ----------------------------------------------------------------------------------
% Plot
% ----------------------------------------------------------------------------------
figure(2);clf;
x = (1:9)/9;
ha = tight_subplot(5,5,[.0 .0],[.0 .0],[.0 .0]);
for i = 1:5
	for j = 1:5
		axes(ha(i*5-5+j));
		h = plot(x, C(:,i,j));
		ylim([0,1.2]);
		xlim([min(x), max(x)]);
		set(gca,'XTick',[])
		set(gca,'YTick',[])
	end
end

最强对角线规则

clc;
E = [1,0.6,0,0,0,0,0,0,0;0.2,0.6,1,0.6,0.2,0,0,0,0;0,0,0.2,0.6,1,0.6,0.2,0,0;0,0,0,0,0.2,0.6,1,0.6,0.2;0,0,0,0,0,0,0.2,0.6,1];
EC = E;
U = E;

% ----------------------------------------------------------------------------------
% Calculate R
% Deduct relationship
% ----------------------------------------------------------------------------------
R = zeros(81,9);
for i = 1:5
	A = E(i,:)';
	B = EC(i,:);
	C = U(i,:);
	AB = min(repmat(A,1,9), repmat(B,9,1));
	AB = reshape(AB, [81,1]);
	RC = min(repmat(AB,1,9), repmat(C, 81,1));
	R = max(R,RC);
end

% ----------------------------------------------------------------------------------
% Calculate C
% Relationship induction
% ----------------------------------------------------------------------------------

C = zeros(9,5,5);
for i = 1:5
	for j = 1:5
		A = E(i,:)';
		B = EC(j,:);
		AB = min(repmat(A,1,9), repmat(B,9,1));
		AB = reshape(AB, [81,1]);
		C(:,i,j) = max(min(repmat(AB, 1, 9), R));
	end
end

% ----------------------------------------------------------------------------------
% Plot
% ----------------------------------------------------------------------------------
figure(2);clf;
x = (1:9)/9;
ha = tight_subplot(5,5,[.0 .0],[.0 .0],[.0 .0]);
for i = 1:5
	for j = 1:5
		axes(ha(i*5-5+j));
		h = plot(x, C(:,i,j));
		ylim([0,1.2]);
		xlim([min(x), max(x)]);
		set(gca,'XTick',[])
		set(gca,'YTick',[])
	end
end

模糊合成的定义

设\(P\)是\(U\times V\) 上的模糊关系，\(Q\)是\(V\times W\)上的模糊关系，则\(R\)是\(U\times W\)上的模糊关系，它是\(P\circ Q\)的合成，其隶属函数被定义为

\[\mu_{R}\left(u,w\right)\Leftrightarrow\mu_{P,Q}\left(u,w\right)=\vee_{v\in V}\left\{ \mu_{P}\left(u,v\right)\wedge\mu_{Q}\left(v,w\right)\right\}
\]

若式中牌子\(\wedge\)代表“取小–\(\min\)”，\(\vee\)代表“取大–\(\max\)”，这种合成关系即为最大值\(\cdot\)最小值合成，合成关系\(R=P\circ Q\)。

示例：

\[A=\begin{bmatrix}{0.4} & {0.5} & {0.6}\\
{0.1} & {0.2} & {0.3}
\end{bmatrix},B=\begin{bmatrix}0.1 & 0.2\\
0.3 & 0.4\\
0.5 & 0.6
\end{bmatrix}.
\]

则\(A\circ B=\begin{bmatrix}0.5 & 0.6\\
0.3 & 0.3
\end{bmatrix}\), \(B\circ A=\begin{bmatrix}{0.1} & {0.2} & {0.2}\\
{0.3} & {0.3} & {0.3}\\
{0.4} & {0.5} & {0.5}
\end{bmatrix}\)。

有定义为

\[A\times B = A^\mathrm{T}\circ B.
\]

模糊推导示例

已知一个双输入单输出的模糊系统，其输入量为\(x\)和\(y\),输出量为\(z\)，其输入输出的关系可用如下两条模糊规则描述：

• \(R_{1}\):如果\(x\)是\(A_{1}\) and \(y\)是\(B_{1}\)，则\(z\)是\(C_{1}\)

• \(R_{2}\):如果\(x\)是\(A_{2}\) and \(y\)是\(B_{2}\)，则\(z\)是\(C_{2}\)

\[\begin{array}{ccc}

{A_{1}}=\frac{1}{{a_{1}}}+\frac{{0.5}}{{a_{2}}}+\frac{0}{{a_{3}}} & {B_{1}}=\frac{1}{{b_{1}}}+\frac{{0.6}}{{b_{2}}}+\frac{{0.2}}{{b_{3}}} & {C_{1}}=\frac{1}{{c_{1}}}+\frac{{0.4}}{{c_{2}}}+\frac{0}{{c_{3}}}\\

{A_{2}}=\frac{0}{{a_{1}}}+\frac{{0.5}}{{a_{2}}}+\frac{1}{{a_{3}}} & {B_{2}}=\frac{{0.2}}{{b_{1}}}+\frac{{0.6}}{{b_{2}}}+\frac{1}{{b_{3}}} & {C_{2}}=\frac{0}{{c_{1}}}+\frac{{0.4}}{{c_{2}}}+\frac{1}{{c_{3}}}

\end{array}
\]

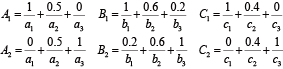
(感觉被恶心到了，不知道为什么这儿的array环境始终出不来)

现已知输入\(x\)为\(A'\), \(y\)为\(B’\),试求输出量。

\[\begin{array}{cc}

A'=\frac{{0.5}}{{a_{1}}}+\frac{1}{{a_{2}}}+\frac{{0.5}}{{a_{3}}}
& B'=\frac{{0.6}}{{b_{1}}}+\frac{1}{{b_{2}}}+\frac{{0.6}}{{b_{3}}}\\
\end{array}
\]

---

\[\begin{aligned}
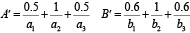
{A_{1}}\times{B_{1}} & =A_{1}^{T}\circ{B_{1}}={\left[{\begin{array}{ccc}
1 & {0.5} & 0\end{array}}\right]^{T}}\left[{\begin{array}{ccc}
1 & {0.6} & {0.2}\end{array}}\right]\\
& =\left[{\begin{array}{ccc}
1 & {0.6} & {0.2}\\
{0.5} & {0.5} & {0.2}\\
0 & 0 & 0
\end{array}}\right]
\end{aligned}
\]

将其按行展开得（把矩阵压扁为一行向量）

\[{R_{1}}=\bar{R}_{{A_{1}}\times{B_{1}}}^{T}\wedge{C_{1}}=\left[{\begin{array}{c}
1\\
{0.6}\\
{0.2}\\
{0.5}\\
{0.5}\\
{0.2}\\
0\\
0\\
0
\end{array}}\right]\wedge\left[{\begin{array}{ccc}
1 & {0.4} & 0\end{array}}\right]=\left[{\begin{array}{ccc}
1 & {0.4} & 0\\
1 & {0.4} & 0\\
{0.2} & {0.2} & 0\\
{0.5} & {0.4} & 0\\
{0.5} & {0.4} & 0\\
{0.2} & {0.2} & 0\\
0 & 0 & 0\\
0 & 0 & 0\\
0 & 0 & 0
\end{array}}\right]
\]

同理：

\[{R_{2}}=\bar{R}_{{A_{2}}\times{B_{2}}}^{T}\wedge{C_{2}}=\left[{\begin{array}{ccc}
0 & 0 & 0\\
0 & 0 & 0\\
0 & 0 & 0\\
0 & {0.2} & {0.2}\\
0 & {0.4} & {0.5}\\
0 & {0.4} & {0.5}\\
0 & {0.2} & {0.2}\\
0 & {0.4} & {0.6}\\
0 & {0.4} & 1
\end{array}}\right]
\]

总的蕴含关系为

\[R={R_{1}}\cup{R_{2}}=\left[{\begin{array}{ccc}
1 & {0.4} & 0\\
{0.6} & {0.4} & 0\\
{0.2} & {0.2} & 0\\
{0.5} & {0.4} & {0.2}\\
{0.5} & {0.4} & {0.5}\\
{0.2} & {0.4} & {0.5}\\
0 & {0.2} & {0.2}\\
0 & {0.4} & {0.6}\\
0 & {0.4} & 1
\end{array}}\right]
\]

计算输入量的模糊集合

\[A'\text{ and }B'=A'\times B'=\left[{\begin{array}{c}
{0.5}\\
1\\
{0.5}
\end{array}}\right]\wedge\left[{\begin{array}{ccc}
{0.6} & 1 & {0.6}\end{array}}\right]=\left[{\begin{array}{ccc}
{0.5} & {0.5} & {0.5}\\
{0.6} & 1 & {0.6}\\
{0.5} & {0.5} & {0.5}
\end{array}}\right]
\]

\[\bar{R}_{A'\times B'}^{T}=\left[{\begin{array}{ccccccccc}
{0.5} & {0.5} & {0.5} & {0.6} & 1 & {0.6} & {0.5} & {0.5} & {0.5}\end{array}}\right]
\]

\[C'=\bar{R}_{A'\times B'}\circ R=\left[{\begin{array}{ccc}
{0.5} & {0.4} & {0.5}\end{array}}\right]
\]

\[C'=\frac{{0.5}}{{c_{1}}}+\frac{{0.4}}{{c_{2}}}+\frac{{0.5}}{{c_{3}}}
\]