扩展KMP笔记

KMP能计算一个字符串的每个位置前最长公共前缀后缀

扩展KMP可以用来计算两个字符串间的最长公共前缀后缀的……

不过为了计算这个需要绕些弯路

已知字符串$S$和$P$，$S$的长度为$n$，$P$的长度为$m$

扩展KMP实际是计算$E$数组，设$E[i]$为字符串$S[i..n-1]$与字符串$P$的最大公共前缀

尝试数学归纳法

$E[0]$显然只能直接依次比对，因为什么信息都没有

假设$E[0]\sim E[i-1]$都计算出来了，现在计算$E[i]$

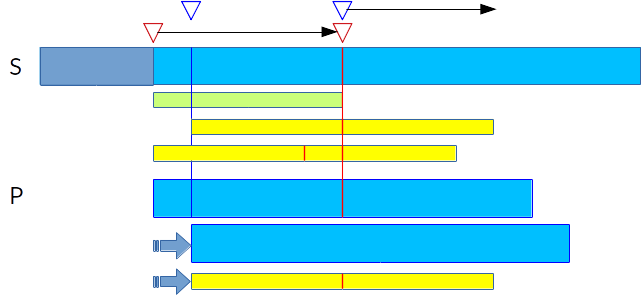
不妨= =，利用$E[i-1]$的信息，第二行的矩形的宽度表示$E[i-1]$，只有这个信息是不够的，否则计算$E[i]$还是需要重复跑计算$E[i-1]$跑过的距离

假设有“$P[i..m-1]$与$P$的最大公共前缀长度”的信息，设为$N[i]$

• 如果$i\geqslant (i-1)+E[i-1]$，说明上个信息对这个没帮助，直接往右跑
• 如果$i+N[1]\geqslant (i-1)+E[i-1]$，由于红线右边的P与S是否相等不确定，因此要舍去红线右边的部分，那么经过如图的变形（第三排和第四排的矩形），可以直接从上一次失败的地方继续（红线处）
• 如果$i+N[1]<(i-1)+E[i-1]$，因为在红线前就失败了，那么直接就可以得到$E[i]=N[1]$

由于第一种情况中仍然可能重复对比$S$和$P$，$E[i-1]$可能不是最好的选择，那么我们就选红线最靠右的$E[k]$来计算$E[i]$

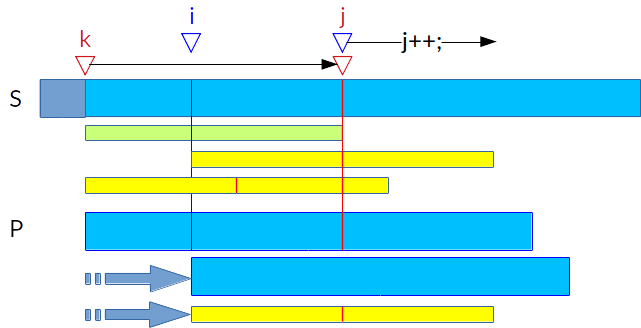
• 如果$i\geqslant j$，说明上个信息对这个没帮助，直接往右跑
• 如果$i+N[i-k]\geqslant j$，由于红线右边的P与S是否相等不确定，因此要舍去红线右边的部分，那么经过如图的变形（第三排和第四排的矩形），可以直接从上一次失败的地方继续（红线处）
• 如果$i+N[i-k]< j$，因为在红线前就失败了，那么直接就可以得到$E[i]=N[i]$

这样，在知道$N[i]$的情况下，可以$\mathcal{O}(n)$得到$E$数组（因为S与P的比较不会重复），前两种情况可以合并为一个，并且可以省去单独计算$E[0]$

代码：

inline void getE() {
    int k = 0, j=0;
    REP(i,0,n) {
        if( i>=j || i+N[i-k] >= j ) {
            if( i>=j ) j=i;
            while( j < n && j - i < m && s[j] == p[j-i]) j++;
            E[i] = j-i;
            k = i;
        } else {
            E[i] = N[i-k];
        }
    }
}

对于$N$数组，和求$E$数组类似

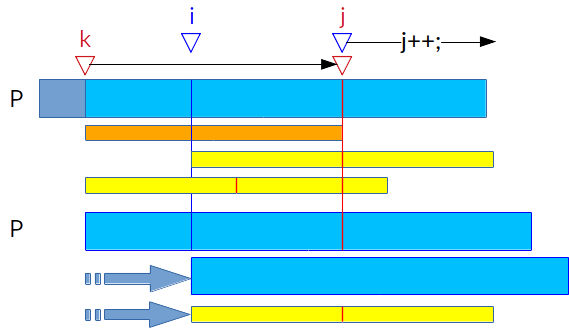
$N[0]=m$，$N[1]$直接计算，假设$N[0]\sim N[i-1]$都求出来了，选红线最靠右的$N[k]$，那么

• 如果$i\geqslant j$，说明上个信息对这个没帮助，直接往右跑
• 如果$i+N[i-k]\geqslant j$，那么直接从上一次失败的地方继续（红线处）
• 如果$i+N[i-k]< j$，因为在红线前就失败了，那么$N[i]=N[i-k]$

代码：

inline void getN() {
    int k = 0, j=0;
    N[0] = m;
    REP(i,1,m) {
        if( i>=j || i+N[i-k] >= j ) {
            if( i>=j ) j=i;
            while( j < m && p[j] == p[j-i]) j++;
            N[i] = j-i;
            k = i;
        } else {
            N[i] = N[i-k];
        }
    }
}

HDU-2594

题目

给两个字符串，第一个字符串与第二个字符串的最长公共前缀后缀

题解

直接套用EXKMP第一个字符串设为p，第二个字符串设为s，找到第一个i，使E[i]=n-i，就可以了

AC代码

#include<cstdio>
#include<cstring>
#include<cassert>
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__),fflush(stdout)
#else
#define DBG(...) (void)0
#endif // sahdsg
using namespace std;
#define REP(r,x,y) for(register int r=(x); r<(y); r++)
#define MAXN 50007
char p[MAXN], s[MAXN];
int N[MAXN], m;
int E[MAXN], n;

inline void getN() {
    int k = 0, j=0;
    N[0] = m;
    REP(i,1,m) {
        if( i>=j || i+N[i-k] >= j ) {
            if( i>=j ) j=i;
            while( j < m && p[j] == p[j-i]) j++;
            N[i] = j-i;
            k = i;
        } else {
            N[i] = N[i-k];
        }
    }
}

inline void getE() {
    int k = 0, j=0;
    REP(i,0,n) {
        if( i>=j || i+N[i-k] >= j ) {
            if( i>=j ) j=i;
            while( j < n && j - i < m && s[j] == p[j-i]) j++;
            E[i] = j-i;
            k = i;
        } else {
            E[i] = N[i-k];
        }
    }
}

int main() {
    #ifdef sahdsg
    freopen("in.txt", "r", stdin);
    #endif // sahdsg
    while(~scanf("%s%s", p,s)) {
        n=strlen(s),m=strlen(p);
        getN();
        getE();
        int t=-1;
//        REP(i,0,n) DBG("%d ", E[i]);
        REP(i,0,n) {
            if(E[i]==n-i) {
                t=i;
                break;
            }
        }
        if(~t) {
            printf("%s %d\n", s+t, n-t);
        } else puts("0");
    }

    return 0;
}