题面：

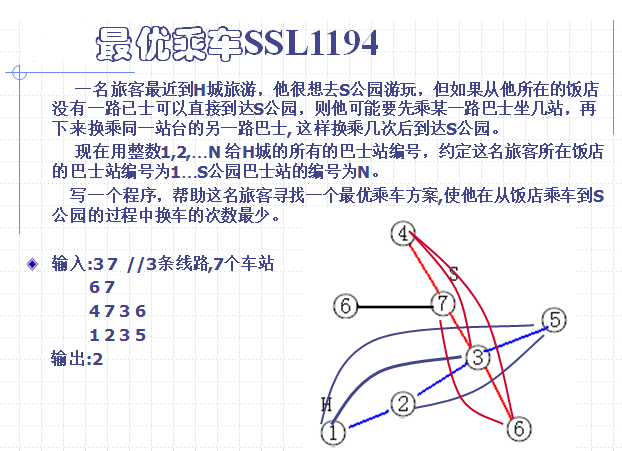
正文：

把每个边用链式前向星存起来，边权为\(1\)，就可以愉♂快♂地最短路了

【SSL1194】最优乘车的更多相关文章

  1. 1722 最优乘车 1997年NOI全国竞赛

    题目描述 Description H城是一个旅游胜地,每年都有成千上万的人前来观光.为方便游客,巴士公司在各个旅游景点及宾馆,饭店等地都设置了巴士站并开通了一些单程巴上线路.每条单程巴士线路从某个巴士 ...

  2. noi 1997 最优乘车

    H城是一个旅游胜地,每年都有成千上万的人前来观光.为方便游客,巴士公司在各个旅游景点及宾馆,饭店等地都设置了巴士站并开通了一些单程巴上线路.每条单程巴士线路从某个巴士站出发,依次途经若干个巴士站,最终 ...

  3. HN0I2000最优乘车 (最短路变形)

    HN0I2000最优乘车 (最短路变形) 版权声明:本篇随笔版权归作者YJSheep(www.cnblogs.com/yangyaojia)所有,转载请保留原地址! [试题]为了简化城市公共汽车收费系 ...

  4. [BFS]最优乘车

    最优乘车 题目描述 HH 城是一个旅游胜地,每年都有成千上万的人前来观光.为方便游客,巴士公司在各个旅游景点及宾馆,饭店等地都设置了巴士站并开通了一些单程巴上线路.每条单程巴士线路从某个巴士站出发,依 ...

  5. AcWing 920. 最优乘车

    H城是一个旅游胜地,每年都有成千上万的人前来观光. 为方便游客,巴士公司在各个旅游景点及宾馆,饭店等地都设置了巴士站并开通了一些单程巴士线路. 每条单程巴士线路从某个巴士站出发,依次途经若干个巴士站, ...

  6. 题解【洛谷P5767】[NOI1997]最优乘车

    题面 一道很经典的最短路模型转换问题. 考虑如何建图. 我们可以发现,对于每一条公交线路,可以将这条线路上 可以到达的两个点 连一条权值为 \(1\) 的边. 获取一条公交线路上的每一个点可以使用读取 ...

  7. zzuoj 10408: C.最少换乘【最短路dijkstra】

    10408: C.最少换乘 Time Limit: 2 Sec  Memory Limit: 128 MBSubmit: 31  Solved: 8[Submit][Status][Web Board ...

  8. nyoj 1238 最少换乘（dijkstra）

    描述 欧洲某城是一个著名的旅游胜地,每年都有成千上万的人前来观光旅行.Dr. Kong决定利用暑假好好游览一番.. 年轻人旅游不怕辛苦,不怕劳累,只要费用低就行.但Dr. Kong年过半百,他希望乘坐 ...

  9. 第八届河南省赛C.最少换乘（最短路建图）

    C.最少换乘 Time Limit: 2 Sec  Memory Limit: 128 MB Submit: 94  Solved: 25 [Submit][Status][Web Board] De ...

随机推荐

  1. 【IT教程-Oracle】尚观Oracle白金级入门教程

    链接: https://pan.baidu.com/s/1GMncQN6mpgaH3hZQjGelaA 提取码: qu6j

  2. 使用position设置经典的网站前端结构

    能脱离文档流的设置: float:left/right position:absolute; 绝对定位 position:fixed; 固定定位 //搞清楚position的属性值的意思就容易明白 使 ...

  3. [模板]tarjan——最后通牒

    这么久了我还是不会板子,你们随便笑话我吧. 再不会打我实在是无能为力了. 这篇博客写的像个智障一样...写它的目的就是自嘲? 才不是,为了方便查阅,因为我真的记不住. 对于割边,要存储该点入边的编号, ...

  4. egret Tiledmap编写障碍物的思路

    egret Tiledmap编写障碍物的思路 获取控制对象下一刻移动的坐标,将其转换成瓦片坐标,如果getTileGIDAt(根据瓦片坐标获取瓦片id)的值不为0,说明对象将要移动的位置有障碍物,不做 ...

  5. Spring注解之@RestControllerAdvice

    前言 前段时间部门搭建新系统,需要出异常后统一接口的返回格式,于是用到了Spring的注解@RestControllerAdvice.现在把此注解的用法总结一下. 用法 首先定义返回对象Respons ...

  6. Ubuntu18.04.3 LTS初体验

    安装系统 想来虚拟机安装太慢,正好有一台旧电脑,干脆整个乌班图系统. 启动盘工具:UltraISO,老牌工具了. 上官网下载ISO镜像文件: https://cn.ubuntu.com/downloa ...

  7. 树莓派debian配置lamp[解决Apache不显示php网页]

    Apache + MySql + Php． 1.安装Apache Apache可以用下面的命令来安装 sudo apt-get install apache2 Apache默认路径是/var/www/ ...

  8. Spring-boot构建多模块依赖工程时，maven打包异常：程序包xxx不存在

    在qizhi项目改版的时候, 所有代码都迁移好了, 但是compile的时候报程序包*****不存在, 具体到某一个类就是: 找不到符号. 下面这篇文章是正解 http://hbxflihua.ite ...

  9. nyoj 26-孪生素数问题(打表)

    26-孪生素数问题 内存限制:64MB 时间限制:3000ms Special Judge: No accepted:10 submit:43 题目描述: 写一个程序,找出给出素数范围内的所有孪生素数 ...

  10. ssm 不能将查询的结果返回到界面的一个原因

    * 在controller类中,应先定义一个ArrayList的集合即就是: List<Product> defaultProductList = new ArrayList(); // ...