浅谈c++中的KMP

百度上一些关于KMP算法的一些基本介绍

所谓KMP，其实就是一种经过改进的模式串匹配算法（即在原串A中查找是否存在模式串B）

通常情况下，我们是这样匹配的

---

串A    X Y Z X X Y Z X Y

串B    X Y Z X Y

串A    X Y Z X X Y Z X Y

串B       X Y Z X Y

……

串A   X Y Z X X Y Z X Y

串B                 X Y Z X Y

（其中红色代表第一次失去匹配的位置）

---

很明显这样匹配是非常低效的

为了优化这种算法，我们考虑令每次将B串右移的位置尽可能长

那么现在问题来了

移动到哪里才算最长？？

---

首先我们保证两个原则：

（1）保证不会漏掉解

（2）向右移尽可能长

首先我们为了右移尽量长，采用从右向左贪心的方式，并设从失配位置到移动位置的距离为k，要求满足B[1~k]==B[j-k~j]

由于前j位均已匹配，所以A[j-k~j]==B[j-k~j]

为了保证移动结束后字符串在可预见的范围内均已匹配，要求A[j-k~j]==B[1~k]

大概就是这样：（图中i、j为失配位置）

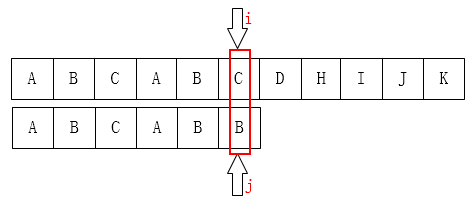
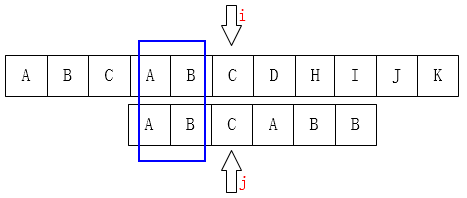（此时k=2）

为了保证不会漏掉解，假设B串头指针移动前为j1，移动后为j2

若j1~j2范围内存在可以匹配到B的子串，那么设这个子串开始的指针为j3，满足j3~j3+strlen(B)==B

那么此时失配位置应在j3,不在原失配位置

注意如果当j<0时仍然找不到匹配位置应从i后面寻找位置进行匹配

---

但这样依然很慢所以我们进入重点

对于每个k来讲很明显只和B串有关

所以我们利用一个nxt数组 nxt[j]表示B串前j位对应的k

这其实就是两个B串在互相进行匹配的过程

上代码

---

//这里数组从1开始
j=;
for(i=;i<n;i++)
{
    while(j> && a[i+]!=b[j+]) j=nxt[j];//j未减小到0且不能继续匹配，减小j的值
    if(a[i+]==b[j+]) j++;//能继续匹配，j的值增加
    //若j==0仍不能匹配，由于循环i的值会自动增加
    if(j==m)//找到一处匹配
        printf("%d\n",i+-m+);//输出子串在主串中的位置
    j=nxt[j];//继续匹配
} 

这是代码1

匹配，输出位置

//这里数组从1开始
j=;
for(i=;i<n;i++)
{
    while(j> && a[i+]!=b[j+]) j=nxt[j];//j未减小到0且不能继续匹配，减小j的值
    if(a[i+]==b[j+]) j++;//能继续匹配，j的值增加
    //若j==0仍不能匹配，由于循环i的值会自动增加
    if(j==m)//找到一处匹配
    {
        printf("%d\n",i+-m+);//输出子串在主串中的位置
        j=;//从头开始匹配，保证不重复
    }
} 

如果若干子串在主串中的位置不能重复，只需将j=nxt[j]改成j=0即可

//这里数组从1开始
p[]=j=;
for(i=;i<m;i++)
{
    while(j> && b[i+]!=b[j+]) j=nxt[j];//j未减小到0且不能继续匹配，退一步
    if(b[i+]==b[j+]) j++;//能继续匹配，j的值增加
    //若j==0仍不能匹配，由于循环i的值会自动增加
    nxt[i+]=j;//nxt数组赋值
} 

这时代码3

预处理nxt数组

有没有觉得预处理和匹配的代码很像？Q_Q