通过机器学习的线性回归算法预测股票走势（用Python实现）

在本人的新书里，将通过股票案例讲述Python知识点，让大家在学习Python的同时还能掌握相关的股票知识，所谓一举两得。这里给出以线性回归算法预测股票的案例，以此讲述通过Python的sklearn库实现线性回归预测的技巧。

本文先讲以波士顿房价数据为例，讲述线性回归预测模型的搭建方式，随后将再这个基础上，讲述以线性预测模型预测股票的实现代码。本博文是从本人的新书里摘取的，新书预计今年年底前出版，敬请大家关注。

正文开始（长文预警）

------------------------------------------------------------------------------------------------------------------------------------------------------

1  波士顿房价数据分析

安装好Python的Sklearn库后，在安装包下的路径中就能看到描述波士顿房价的csv文件，具体路径是“python安装路径\Lib\site-packages\sklearn\datasets\data”，在这个目录中还包含了Sklearn库会用到的其他数据文件，本节用到的是包含在boston_house_prices.csv文件中的波士顿房价信息。打开这个文件，可以看到如图所示的数据。

第1行的506表示该文件中包含506条样本数据，即有506条房价数据，而13表示有13个影响房价的特征值，即从A列到M列这13列的特征值数据会影响第N列MEDV（即房价值），在表13.1中列出了部分列的英文标题及其含义。

波士顿房价文件部分中英文标题一览表

标题名	中文含义	标题名	中文含义
CRIM	城镇人均犯罪率	DIS	到波士顿五个中心区域的加权距离
ZN	住宅用地超过某数值的比例	RAD	辐射性公路的接近指数
INDUS	城镇非零售商用土地的比例	TAX	每 10000 美元的全值财产税率
CHAS	查理斯河相关变量，如边界是河流则为1，否则为0	PTRATIO	城镇师生比例
NOX	一氧化氮浓度	MEDV	是自住房的平均房价
RM	住宅平均房间数
AGE	1940年之前建成的自用房屋比例

从表中可以看到，波士顿房价的数值（即MEDV）和诸如“住宅用地超过某数值的比例”等13个特征值有关。而线性回归要解决的问题是，量化地找出这些特征值和目标值（即房价）的线性关系，即找出如下的k1到k13系数的数值和b这个常量值。

MEDV = k1*CRIM + k2*ZN + … + k13*LITAT + b

上述参数有13个，为了简化问题，先计算1个特征值（DIS）与房价（MEDV）的关系，然后在此基础上讲述13个特征值与房价关系的计算方式。

如果只有1个特征值DIS，它与房价的线性关系表达式如下所示。在计算出k1和b的值以后，如果再输入对应DIS值，即可据此计算MEDV的值，以此实现线性回归的预测效果。

MEDV = k1*DIS + b

2  以波士顿房价数据为案例，搭建含一个特征值的线性预测模型

在下面的OneParamLR.py范例程序中，通过调用Sklearn库中的方法，以训练加预测的方式，推算出一个特征值（DIS）与目标值（MEDV，即房价）的线性关系。

1    # !/usr/bin/env python

2    # coding=utf-8

3    import numpy as np

4    import pandas as pd

5    import matplotlib.pyplot as plt

6    from sklearn import datasets

7    from sklearn.linear_model import LinearRegression

　在上述代码中导入了必要的库，其中第6行和第7行用于导入sklearn相关库。

8    # 从文件中读数据，并转换成DataFrame格式

9    dataset=datasets.load_boston()

10   data=pd.DataFrame(dataset.data)

11   data.columns=dataset.feature_names              # 特征值

12   data['HousePrice']=dataset.target               # 房价，即目标值

13   # 这里单纯计算离中心区域的距离和房价的关系

14   dis=data.loc[0:data['DIS'].size-1,'DIS'].as_matrix()

15   housePrice=data.loc[0:data['HousePrice'].size-1,'HousePrice'].as_matrix()

在第9行中，加载了Sklearn库下的波士顿房价数据文件，并赋值给dataset对象。在第10行通过dataset.data读取了文件中的数据。在第11行通过dataset.feature_name读取了特征值，如前文所述，data.columns对象中包含了13个特征值。在第12行通过dataset.target读取目标值，即MEDV列的房价，并把目标值设置到data的HousePrice列中。

在第14行读取了DIS列的数据，并调用as_matrix方法把读到的数据转换成矩阵中一列的格式，在第15行中，是用同样的方法把房价数值转换成矩阵中列的格式。

16   # 转置一下，否则数据是竖排的

17   dis=np.array([dis]).T

18   housePrice=np.array([housePrice]).T

19   # 训练线性模型

20   lrTool=LinearRegression()

21   lrTool.fit(dis,housePrice)

22   # 输出系数和截距

23   print(lrTool.coef_)

24   print(lrTool.intercept_)

由于当前在dis和housePrice变量中保存是的“列”形式的数据，因此在第16行和第17行中，需要把它们转换成行格式的数据。

在第20行中，通过调用LinearRegression方法创建了一个用于线性回归分析的lrTool对象，在第21行中，通过调用fit方法进行基于线性回归的训练。这里训练的目的是，根据传入的一组特征值dis和目标值MEDV，推算出MEDV = k1*DIS + b公式中的k1和b的值。

调用fit方法进行训练后，ltTool对象就内含了系数和截距等线性回归相关的参数，通过第23行的打印语句输出了系数，即参数k1的值，而第24行的打印语句输出了截距，即参数b的值。

25   # 画图显示

26   plt.scatter(dis,housePrice,label='Real Data')

27   plt.plot(dis,lrTool.predict(dis),c='R',linewidth='2',label='Predict')

28   # 验证数据

29   print(dis[0])

30   print(lrTool.predict(dis)[0])

31   print(dis[2])

32   print(lrTool.predict(dis)[2])

33    

34   plt.legend(loc='best')    # 绘制图例

35   plt.rcParams['font.sans-serif']=['SimHei']

36   plt.title("DIS与房价的线性关系")

37   plt.xlabel("DIS")

38   plt.ylabel("HousePrice")

39   plt.show()

在第26行中，通过调用scatter方法绘制出x值是DIS，y值是房价的诸多散点，第27行则是调用plot方法绘制出DIS和预测结果的关系，即一条直线。

之后就是用Matplotlib库中的方法绘制出x轴y轴文字和图形标题等信息。运行上述代码，即可看到如图所示的结果。

图中各个点表示真实数据，每个点的x坐标是DIS值，y坐标是房价。而红线则表示根据当前DIS值，通过线性回归预测出的房价结果。

下面通过输出的数据，进一步说明图中以红线形式显示的预测数据的含义。通过代码的第23行和24行输出了系数和截距，结果如下。

[[1.09161302]]

[18.39008833]

即房价和DIS满足如下的一次函数关系：MEDV = 1.09161302*DIS + 18.39008833。

从第29行到第32行输出了两组DIS和预测房价数据，每两行是一组，结果如下。

[4.09]

[22.85478557]

[4.9671]

[23.81223934]

在已经得到的公式中，MEDV = 1.09161302*DIS + 18.39008833，把第1行的4.09代入DIS，把第2行的22.85478557代入MEDV，发现结果吻合。同理，把第3行的DIS和第4行MEDV值代入上述公式，结果也吻合。

也就是说，通过基于线性回归的fit方法，训练了lrTool对象，使之包含了相关参数，这样如果输入其他的DIS值，那么ltTool对象根据相关参数也能算出对应的房价值。从可视化的效果来看，用DIS预测MEDV房价的效果并不好，原因是毕竟只用了其中一个特征值。不过，通过这个范例程序，还是可以看出基于线性回归实现预测的一般步骤：根据一组（506条）数据的特征值（本范例中是DIS）和目标值（房价），调用fit方法训练ltTool等线性回归中的对象，让它包含相关系数，随后再调用predict方法，根据由相关系数组成的公式，通过计算预测目标结果。

3  以波士顿房价数据为案例，实现基于多个特征值的线性回归

如果要用到波士顿房价范例中13个特征值来进行预测，那么对应的公式如下，这里要做的工作是，通过fit方法，计算如下的k1到k13系数以及b截距值。

MEDV = k1*CRIM + k2*ZN + … + k13*LITAT + b

在下面的MoreParamLR.py范例程序中，实现用13个特征值预测房价的功能。

1    # !/usr/bin/env python

2    # coding=utf-8

3    from sklearn import datasets

4    from sklearn.linear_model import LinearRegression

5    import matplotlib.pyplot as plt

6    # 加载数据

7    dataset = datasets.load_boston()

8    # 特征值集合，不包括目标值房价

9    featureData = dataset.data

10   housePrice = dataset.target

在第7行中加载了波士顿房价的数据，在第9行和第10行分别把13个特征值和房价目标值放入featureData和housePrice这两个变量中。

11   lrTool = LinearRegression()

12   lrTool.fit(featureData, housePrice)

13   # 输出系数和截距

14   print(lrTool.coef_)

15   print(lrTool.intercept_)

上述代码和前文推算一个特征值和目标值关系的代码很相似，只不过在第12行的fit方法中，传入的特征值是13个，而不是1个。在第14行和第15行的程序语句同样输出了各项系数和截距数值。

16   # 画图显示

17   plt.scatter(housePrice,housePrice,label='Real Data')

18   plt.scatter(housePrice,lrTool.predict(featureData),c='R',label='Predicted Data')

19   plt.legend(loc='best')    # 绘制图例

20   plt.rcParams['font.sans-serif']=['SimHei']

21   plt.xlabel("House Price")

22   plt.ylabel("Predicted Price")

23   plt.show()

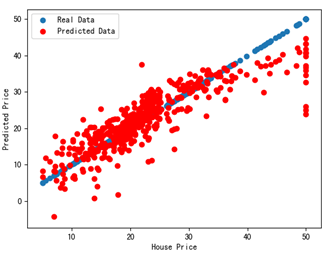
在第17行绘制了x坐标和y坐标都是房价值的散列点，这些点表示原始数据，在第19行绘制散列点时，x坐标是原始房价，y坐标是根据线性回归推算出的房价。

运行上述代码，即可看到如图所示的结果。其中蓝色散列点表示真实数据，红色散列点表示预测出的数据，和图13-4相比，预测出的房价结果数据更靠近真实房价数据，这是因为这次用了13个特征值来预测，而之前只用了其中一个特征数据来预测。

另外，从控制台中可以看到由第14行和15行的程序语句打印出的各项系数和截距。

1    [-1.08011358e-01  4.64204584e-02  2.05586264e-02  2.68673382e+00  -1.77666112e+01  3.80986521e+00 6.92224640e-04 -1.47556685e+00  3.06049479e-01 -1.23345939e-02 -9.52747232e-01  9.31168327e-03 -5.24758378e-01]

2    36.459488385089855

其中，第1行表示13个特征值的系数，而第2行表示截距。代入上述系数，即可看到如下的13个特征值与目标房价的对应关系——预测公式。得出如下的公式后，再输入其他的13个特征值，即可预测出对应的房价。

MEDV = -1.08011358e-01*CRIM + 4.64204584e-02*ZN + … + -5.24758378e-01*LITAT + 36.459488385089855

4  激动人心的时刻，预测股票价格

在这里，将在下面的predictStockByLR.py范例程序中，根据股票历史的开盘价、收盘价和成交量等特征值，从数学角度来预测股票未来的收盘价。

1    # !/usr/bin/env python

2    # coding=utf-8

3    import pandas as pd

4    import numpy as np

5    import math

6    import matplotlib.pyplot as plt

7    from sklearn.linear_model import LinearRegression

8    from sklearn.model_selection import train_test_split

9    # 从文件中获取数据

10   origDf = pd.read_csv('D:/stockData/ch13/6035052018-09-012019-05-31.csv',encoding='gbk')

11   df = origDf[['Close', 'High', 'Low','Open' ,'Volume']]

12   featureData = df[['Open', 'High', 'Volume','Low']]

13   # 划分特征值和目标值

14   feature = featureData.values

15   target = np.array(df['Close'])

第10行的程序语句从包含股票信息的csv文件中读取数据，在第14行设置了特征值是开盘价、最高价、最低价和成交量，同时在第15行设置了要预测的目标列是收盘价。在后续的代码中，需要将计算出开盘价、最高价、最低价和成交量这四个特征值和收盘价的线性关系，并在此基础上预测收盘价。

16   # 划分训练集，测试集

17   feature_train, feature_test, target_train ,target_test = train_test_split(feature,target,test_size=0.05)

18   pridectedDays = int(math.ceil(0.05 * len(origDf)))    # 预测天数

19   lrTool = LinearRegression()

20   lrTool.fit(feature_train,target_train)   # 训练

21   # 用测试集预测结果

22   predictByTest = lrTool.predict(feature_test)

第17行的程序语句通过调用train_test_split方法把包含在csv文件中的股票数据分成训练集和测试集，这个方法前两个参数分别是特征列和目标列，而第三个参数0.05则表示测试集的大小是总量的0.05。该方法返回的四个参数分别是特征值的训练集、特征值的测试集、要预测目标列的训练集和目标列的测试集。

第18行的程序语句计算了要预测的交易日数，在第19行中构建了一个线性回归预测的对象，在第20行是调用fit方法训练特征值和目标值的线性关系，请注意这里的训练是针对训练集的，在第22行中，则是用特征值的测试集来预测目标值（即收盘价）。也就是说，是用多个交易日的股价来训练lrTool对象，并在此基础上预测后续交易日的收盘价。至此，上面的程序代码完成了相关的计算工作。

23   # 组装数据

24   index=0

25   # 在前95%的交易日中，设置预测结果和收盘价一致

26   while index < len(origDf) - pridectedDays:

27       df.ix[index,'predictedVal']=origDf.ix[index,'Close']

28       df.ix[index,'Date']=origDf.ix[index,'Date']

29       index = index+1

30   predictedCnt=0

31   # 在后5%的交易日中，用测试集推算预测股价

32   while predictedCnt<pridectedDays:

33       df.ix[index,'predictedVal']=predictByTest[predictedCnt]

34       df.ix[index,'Date']=origDf.ix[index,'Date']

35       predictedCnt=predictedCnt+1

36       index=index+1

在第26行到第29行的while循环中，在第27行把训练集部分的预测股价设置成收盘价，并在第28行设置了训练集部分的日期。

在第32行到第36行的while循环中，遍历了测试集，在第33行的程序语句把df中表示测试结果的predictedVal列设置成相应的预测结果，同时也在第34行的程序语句逐行设置了每条记录中的日期。

37   plt.figure()

38   df['predictedVal'].plot(color="red",label='predicted Data')

39   df['Close'].plot(color="blue",label='Real Data')

40   plt.legend(loc='best')    # 绘制图例

41   # 设置x坐标的标签

42   major_index=df.index[df.index%10==0]

43   major_xtics=df['Date'][df.index%10==0]

44   plt.xticks(major_index,major_xtics)

45   plt.setp(plt.gca().get_xticklabels(), rotation=30)

46   # 带网格线，且设置了网格样式

47   plt.grid(linestyle='-.')

48   plt.show()

在完成数据计算和数据组装的工作后，从第37行到第48行程序代码的最后，实现了可视化。

第38行和第39行的程序代码分别绘制了预测股价和真实收盘价，在绘制的时候设置了不同的颜色，也设置了不同的label标签值，在第40行通过调用legend方法，根据收盘价和预测股价的标签值，绘制了相应的图例。

从第42行到第45行设置了x轴显示的标签文字是日期，为了不让标签文字显示过密，设置了“每10个日期里只显示1个”的显示方式，并且在第47行设置了网格线的效果，最后在第48行通过调用show方法绘制出整个图形。运行本范例程序，即可看到如图所示的结果。

从图中可以看出，蓝线表示真实的收盘价（图中完整的线），红线表示预测股价（图中靠右边的线。因为本书黑白印刷的原因，在书中读者看不到蓝色和红色，请读者在自己的计算机上运行这个范例程序即可看到红蓝两色的线）。虽然预测股价和真实价之间有差距，但涨跌的趋势大致相同。而且在预测时没有考虑到涨跌停的因素，所以预测结果的涨跌幅度比真实数据要大。

5 系列文总结和版权说明

本文是给程序员加财商系列，之前的系列文如下：

    在我的新书里，尝试着用股票案例讲述Python爬虫大数据可视化等知识   

 

    以股票RSI指标为例，学习Python发送邮件功能（含RSI指标确定卖点策略）

 

    以预测股票涨跌案例入门基于SVM的机器学习

 

    用python的matplotlib和numpy库绘制股票K线均线和成交量的整合效果（含量化验证交易策略代码） 

 

    用python的matplotlib和numpy库绘制股票K线均线的整合效果（含从网络接口爬取数据和验证交易策略代码） 

    本文力争做到详细，比如代码按行编号，并针对行号详细解释，且图文并茂，所以如果大家感觉可以，请尽量帮忙推荐一下。本文的内容即将出书，在出版的书里，是用股票案例和大家讲述Python入门时的知识点，敬请期待。    

有不少网友转载和想要转载我的博文，本人感到十分荣幸，这也是本人不断写博文的动力。关于本文的版权有如下统一的说明，抱歉就不逐一回复了。

1 本文可转载，无需告知，转载时请用链接的方式，给出原文出处，别简单地通过文本方式给出，同时写明原作者是hsm_computer。

2 在转载时，请原文转载 ，谢绝洗稿。否则本人保留追究法律责任的权利。