SPSS学习笔记参数检验—单样本t检验

单样本t检验

目的：利用来自总体的样本数据，推断该总体的均值是否与指定的检验值存在差异。

适用条件：样本来自的总体应服从或者近似服从正态分布。

注：当样本量n比较大时：由中心极限定理得知，即使原数据不服从正态分布，但是样本量足够大，他的样本均数抽样分布仍然是正态的，因此，在样本量很大的情况下很少考虑单样本t检验的适用条件；

当样本量n比较小时，总体应服从正态分布；

总结：只要数据没有很强烈的偏态，单样本t检验的分析结果都是稳定的。

案例分析：

案例描述：推断信用卡刷卡金额的平均值是否不低于3000元。（数据来源：《统计分析与SPSS的应用》薛薇 第五章）

题目分析：该问题涉及的是单个总体（信用卡刷卡金额），进行总体均值检验，同时总体可近似认为服从正态分布（正态分布检验），因此用单样本t检验。

案例步骤：

提出原假设：信用卡刷卡金额的平均值不显著低于3000元。

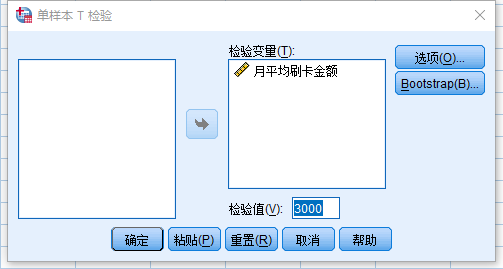
界面菜单操作：分析—比较均值—单样本T检验—选择检验的变量—得出结果

关键步骤截图：

检验值应填3000

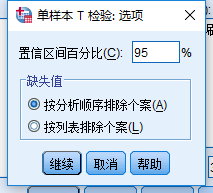
缺失值的处理：

（1）按分析顺序排除个案：只针对计算变量的缺失值，剔除该变量的个案；

（2）按列表排除个案：针对列表中所有变量的缺失值，一旦发现某个变量有缺失值，直接剔除该个案。

结果分析：

单个样本统计量
	N	均值	标准差	均值的标准误
月平均刷卡金额	500	4781.8786	7418.71785	331.77515

均值的标准误：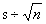

单个样本检验
	检验值 = 3000
	t	df	Sig.(双侧)	均值差值	差分的 95% 置信区间
					下限	上限
月平均刷卡金额	5.371	499	.000	1781.87860	1130.0302	2433.7270

t统计量的数学定义：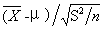

df：自由度（n-1）

Sig（双侧）：双侧概率P-值；

注：

（1）当问题使用的是双侧检验方法时，比较ɑ（一般取0.05）和p；当p<ɑ时，拒绝原假设，接受备假设。当p>=ɑ，则相反。

（2）当问题使用的是单侧检验方法时，比较ɑ（一般取0.05）和p/2；当p/2<ɑ时，拒绝原假设，接受备假设。当p/2>=ɑ，则相反。

平方米无显著差异，这时候可以从两个方向拒绝原假设：实际住房面积的平均值远大于或者远小于20平方米。

元有明显差异，而且远远高于3000元。

置信区间：95%的置信区间为（1130.0302，2433.7270），我们有95%的把握认为月刷卡金额的平均值在4130.0302~5433.7270之间。

参考书籍：

《统计分析与SPSS的应用》（第五版）薛薇

《SPSS统计分析从零开始》吴骏

《SPSS统计分析基础教程》张文彤