轰炸行动(bomb)：tarjan，拓扑排序

考场上看错题，没什么好说的。

然而它就是一个大板子。

发的题解勉强还能看。但是我还想再讲讲。

题目的表述是，如果从A能直接或间接到B，那么就不能同时轰炸A和B。

那么我们从图里随便拽出一条有向路径，从这条路径中随意挑2个点AB，那么要么能从A到B要么从B到A

那么你任意挑出的这两个点只要不是同一个点那么就不能同时轰炸。

带下划线的那一段有什么用呢？它的正确性是显然的。

我所说的“有向路径”没有加任何附加限制，所以可以包括环，环上转几圈就可能出现同一个点呗。

我们考虑单纯的一个环。那么它上的每一个都要单独炸一次。

再考虑单纯的一条路径，那么路径上的每一个点也需要单独炸一次。

如果一个路径进入了一个环，那么这上面的点也必须单独炸一次（路径上的点可以到达环上的任意点）。

如果一个环引出了一个路径，那么环上的点亦可到路径上，都要单独炸一次。

综上，就是要找出一条路径使它上面的不同的点尽量多，不同的点的个数即为答案。

上面那一堆话里已经包括了这个意思：环上的每个点都会给路径长度增加1，且对联通性没有影响。

所以考虑tarjan缩完强联通分量后就没有环了，只不过环变成了权值等于环中点数的一个大点而已

其余普通点的权值为1。现在的问题就变成了在一个DAG里找一条路径使它上面的点权和最大。

不能dfs，因为这是有向的DAG，虽然不是环但也不是树，它可以长得很恶心。

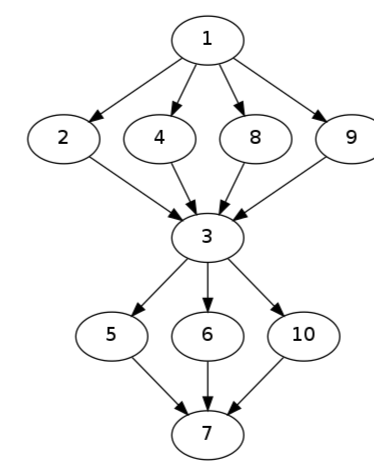
在这个恶心图里面跑dfs就会多次重复地经过3和3下面的点导致大量浪费。

可以倒着搜加个记忆化什么的，然而一个拓扑排序会更方便一些。

 #include<bits/stdc++.h>
 using namespace std;
 map<int,int>mm;
 int n,m,fir[],l[],to[],cnt=,dfn[],low[];
 int _fir[],_l[],_to[],_cnt,w[],in[];
 int sta[],ins[],tim,top,bl[],cnt_scc,ans,dis[];
 int q[],t;
 void connect(int a,int b){l[++cnt]=fir[a];fir[a]=cnt;to[cnt]=b;}
 void _connect(int a,int b){_l[++_cnt]=_fir[a];_fir[a]=_cnt;_to[_cnt]=b;in[b]++;}
 void tarjan(int p){
     dfn[p]=low[p]=++tim;sta[++top]=p;ins[p]=;
     for(int i=fir[p];i;i=l[i])
         if(!dfn[to[i]])tarjan(to[i]),low[p]=min(low[p],low[to[i]]);
         else if(ins[to[i]])low[p]=min(low[p],low[to[i]]);
     if(dfn[p]==low[p]){
         w[++cnt_scc]++;
         while(sta[top]!=p)ins[sta[top]]=,bl[sta[top--]]=cnt_scc,w[cnt_scc]++;
         top--;bl[p]=cnt_scc;ins[p]=;
     }
 }
 signed main(){
     scanf("%d%d",&n,&m);
     for(int i=,a,b;i<=m;++i)scanf("%d%d",&a,&b),connect(a,b);
     for(int i=;i<=n;++i)if(!dfn[i])tarjan(i);
     for(int i=;i<=n;++i)for(int j=fir[i];j;j=l[j])
         if(bl[i]!=bl[to[j]])_connect(bl[i],bl[to[j]]);
     for(int i=;i<=cnt_scc;++i)if(!in[i])q[++t]=i;
     for(int h=;h<=t;++h){
         int dt=dis[q[h]]+w[q[h]];ans=max(ans,dt);
         for(int i=_fir[q[h]];i;i=_l[i]){
             in[_to[i]]--;dis[_to[i]]=max(dis[_to[i]],dt);
             if(!in[_to[i]])q[++t]=_to[i];
         }
     }
     printf("%d\n",ans);
 }

码量其实也不大