P4568 [JLOI2011]飞行路线(分层图)
机房dalao推荐写的。。。(标签分层图)
经过前几题的分层图的洗礼,我深刻地体会到了分层图的优点和好处(主要是不想打dp....)
先说题吧....
很明确,模型是最短路,但是,怎么跑k个,是个问题....
解题过程:
1、先跑最短路,记录路径,然后找路径上的k条最长边,删掉
tips:贪心,很容易hack掉。
2、建两层的分层图(以前打的都是两层居多)
tips:会跑出0来....
solution:
主要就是:怎么连边喽....一开始老是卡住
连边有2种情况:
- 同一层之间的边,边权为题目给的边权,同层之间连
- 层与层之间,一个点连到下一层的它对应的出点,边权为0,为单向边
一共K层,上层可以跑到下层的出点,却不能回去,这就是一次免票。
然后跑最短路,最后查t+n*k那个点的dis就可以了。
- for(int i=;i<=m;i++)
- {
- int x,y,z;
- x=read();y=read();z=read();
- addedge(x,y,z);
- addedge(y,x,z);
- for(int j=;j<=k;j++)
- {
- addedge(x+n*j,y+n*j,z);
- addedge(y+n*j,x+n*j,z);
- addedge(x+(j-)*n,y+j*n,);
- addedge(y+(j-)*n,x+j*n,);
- }
- }
如上,分层连边。
之后就是一个spfa的事了(然而我各种常数(畜生)优化+O2卡到比旁边dalao快600ms的地步哈哈哈哈)
值得注意:
1、最后要把每一层的t点连在一起,因为如果在第二层就跑到了最短,在最后一层的t并不能查到正确答案
2、一共有k+1层,所以初始化dis要k+1层,因为这个卡了一小会...
- #include<bits/stdc++.h>
- using namespace std;
- const int maxn=6e6+;
- int n,m,k;
- int s,t;
- inline int read()
- {
- int x=,f=;char s=getchar();
- while(s>''||s<''){if(s=='-')f=-;s=getchar();}
- while(s<=''&&s>=''){x=x*+s-'';s=getchar();}
- return x*f;
- }
- struct edge
- {
- int to,next,dis;
- }e[maxn];
- int head[maxn],cnt;
- inline void addedge(int from,int to,int dis)
- {
- e[++cnt].next=head[from];
- e[cnt].to=to;
- e[cnt].dis=dis;
- head[from]=cnt;
- }
- int dis[maxn],vis[maxn];
- struct cmp
- {
- bool operator () (int a,int b)
- {
- return dis[a]>dis[b];
- }
- };
- priority_queue < int , vector < int > , cmp > q;
- //queue < int > q;
- void spfa(int s)
- {
- for(int i=;i<=(k+)*n;i++)
- {
- dis[i]=;
- vis[i]=;
- }
- //memset(dis,0x3f,sizeof(dis));
- q.push(s);
- dis[s]=;
- vis[s]=;
- while(!q.empty())
- {
- //cout<<233;
- int u=q.top();
- //int u=q.front();
- q.pop();
- vis[u]=;
- for(int i=head[u];i;i=e[i].next)
- {
- int v=e[i].to;
- if(dis[v]>dis[u]+e[i].dis)
- {
- dis[v]=dis[u]+e[i].dis;
- if(vis[v]==)
- {
- q.push(v);
- vis[v]=;
- }
- }
- }
- }
- }
- int main()
- {
- n=read();
- m=read();
- k=read();
- s=read();
- t=read();
- for(int i=;i<=m;i++)
- {
- int x,y,z;
- x=read();
- y=read();
- z=read();
- addedge(x,y,z);
- addedge(y,x,z);
- for(int j=;j<=k;j++)
- {
- addedge(x+n*j,y+n*j,z);
- addedge(y+n*j,x+n*j,z);
- addedge(x+(j-)*n,y+j*n,);
- addedge(y+(j-)*n,x+j*n,);
- }
- }
- for(int i=;i<=k;i++)
- addedge(t+(i-)*n,t+i*n,);
- spfa(s);
- cout<<dis[t+k*n];//printf("%d",dis[t+k*n]);
- return ;
- }
现在来说一说dp和分层图的关系:
首先,分层图的“层”是什么,它就是dp中的状态。在一些图论题目中,状态不好转移,就可以使用分层图进行转移,不需要再管“从哪转移”这个问题,剩下的最优解直接交给spfa就行了。(最优贸易)
这些状态之间可以互相转移,一般在二维或是以上,可以省去一些不相关状态的枚举,但是因为spfa的广泛枚举性还是会枚举更多“不是最优解”的状态的。
(完)
P4568 [JLOI2011]飞行路线(分层图)的更多相关文章
- P4568 [JLOI2011]飞行路线 分层图
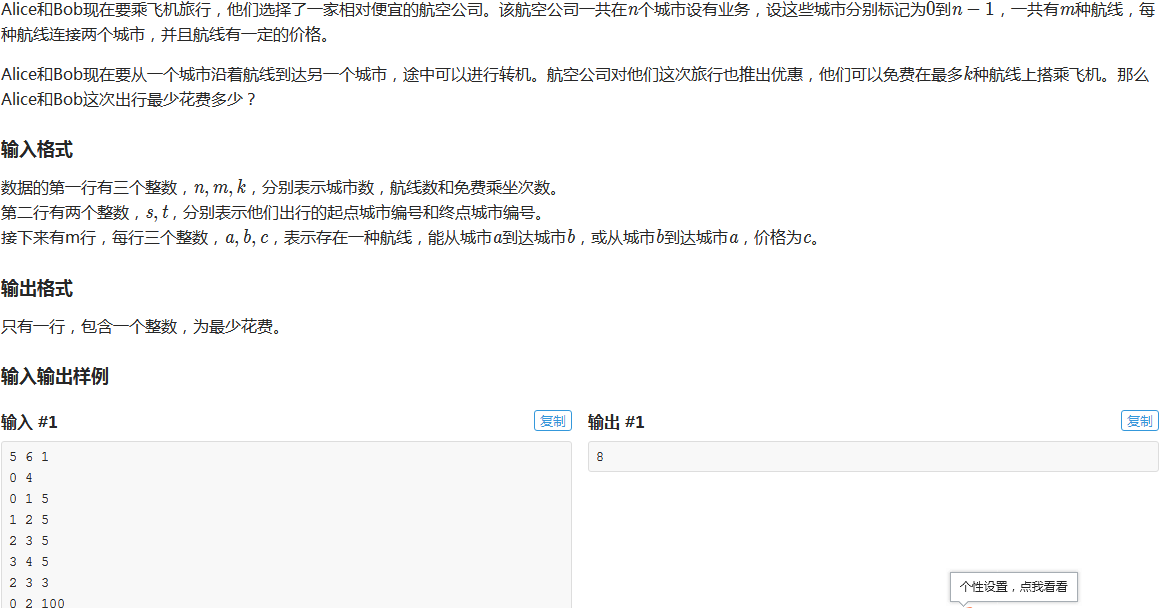
题目描述 Alice和Bob现在要乘飞机旅行,他们选择了一家相对便宜的航空公司.该航空公司一共在nn个城市设有业务,设这些城市分别标记为00到n-1n−1,一共有mm种航线,每种航线连接两个城市,并且 ...
- P4568 [JLOI2011]飞行路线 分层图最短路
思路:裸的分层图最短路 提交:1次 题解: 如思路 代码: #include<cstdio> #include<iostream> #include<cstring> ...
- bzoj2763: [JLOI2011]飞行路线(分层图spfa)
2763: [JLOI2011]飞行路线 Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 3234 Solved: 1235[Submit][Stat ...
- bzoj 2763: [JLOI2011]飞行路线 -- 分层图最短路
2763: [JLOI2011]飞行路线 Time Limit: 10 Sec Memory Limit: 128 MB Description Alice和Bob现在要乘飞机旅行,他们选择了一家相 ...
- BZOJ2763[JLOI2011]飞行路线 [分层图最短路]
2763: [JLOI2011]飞行路线 Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 2523 Solved: 946[Submit][Statu ...
- [BZOJ2963][JLOI2011]飞行路线 分层图+spfa
Description Alice和Bob现在要乘飞机旅行,他们选择了一家相对便宜的航空公司.该航空公司一共在n个城市设有业务,设这些城市分别标记为0到n-1,一共有m种航线,每种航线连接两个城市,并 ...
- BZOJ2763: [JLOI2011]飞行路线(分层图 最短路)
题意 题目链接 Sol 分层图+最短路 建\(k+1\)层图,对于边\((u, v, w)\),首先在本层内连边权为\(w\)的无向边,再各向下一层对应的节点连边权为\(0\)的有向边 如果是取最大最 ...
- 【bzoj2763】[JLOI2011]飞行路线 分层图最短路
题目描述 Alice和Bob现在要乘飞机旅行,他们选择了一家相对便宜的航空公司.该航空公司一共在n个城市设有业务,设这些城市分别标记为0到n-1,一共有m种航线,每种航线连接两个城市,并且航线有一定的 ...
- bzoj 2763 [JLOI2011]飞行路线——分层图
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=2763 分层图两种方法的练习. 1.把图分成k+1层,本层去上面一层的边免费.但空间时间都不算 ...
- bzoj2763 [JLOI2011]飞行路线——分层图
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=2763 构建分层图. 代码如下: 写法1(空间略大)(时间很慢): #include<i ...
随机推荐
- JavaScript:如何获取某一天所在的星期
我们会遇到的需求的是,获取今天或者某一天所在星期的开始和结束日期. 我们这里来获取今天所在星期的始末日期,我们可以通过(new Date).getDay()来获取今天是星期几,然后再通过这个减去或者加 ...
- Java集合框架,你了解多少?相信你看了这篇汇总一目了然!
相信大多数的程序员都知道,Dictionary.Vertor.Stack和Properties这些类被用来存储和操作对象组.但是他们缺少一个核心的主题的. 集合框架设计成要满足以下的几个目标 第一条: ...
- 流水线机制、滑动窗口协议、GBN、SR
一.滑动窗口协议 为了解决停等操作的性能问题(发了一个分组之后一直等到确认了这个分组才发下一个),推出了流水线机制,提供资源利用率.就是允许发送方在收到对方的ACK前,发送多个分组 其中窗口是一个范围 ...
- Fiddler的安装
相关下载软件(链接:https://pan.baidu.com/s/1HFdFNph6FGHOFtZq09ldpg 提取码:3u3l ) fiddler是基于.net环境的,所以需要先安装.net 安 ...
- prototype与 _proto__的关系
prototype与 __ proto__ 都是在这个过程中催生的产物,我们一会儿马上讨论,在这之...做对象即可,那javascript种究竟是通过什么来明确继承关系的呢. 一.构造函数: 构造函数 ...
- HNOI2012 永无乡 无旋Treap
题目描述 永无乡包含 nnn 座岛,编号从 111 到 nnn ,每座岛都有自己的独一无二的重要度,按照重要度可以将这 nnn 座岛排名,名次用 111 到 nnn 来表示.某些岛之间由巨大的桥连接, ...
- 16.Linux yum扩展
1.列出yum源可用的软件仓库 [root@yinwucheng ~]# yum repolist [root@yinwucheng ~]# yum repolist all 查看所有的仓库 ``` ...
- 基于 HTML5 Canvas 的楼宇自控系统
前言 楼宇自控是指楼宇中电力设备,如电梯.水泵.风机.空调等,其主要工作性质是强电驱动.通常这些设备是开放性的工作状态,也就是说没有形成一个闭环回路.只要接通电源,设备就在工作,至于工作状态.进程.能 ...
- win32API多线程编程
win32线程API 在Windows平台下可以通过Windows的线程库来实现多线程编程. 对于多线程程序可以使用Visual Studio调试工具进行调试,也可以使用多核芯片厂家的线程分析调试工具 ...
- Qt乱码的问题
1.在启动应用程序前加入以下代码: //配置字符编码环境,让应用程序支持中文. QTextCodec *codec = QTextCodec::codecForName("System&qu ...
