传送门

先考虑每一个攻击方的龙和被攻击方的龙可以与多少个被攻击方/攻击方的龙匹配。

对于攻击方的龙\(A\)和被攻击方的龙\(B\)，在道路为线段\((C,D)\)的情况下，能够与下图位置的所有对应属性的龙匹配：

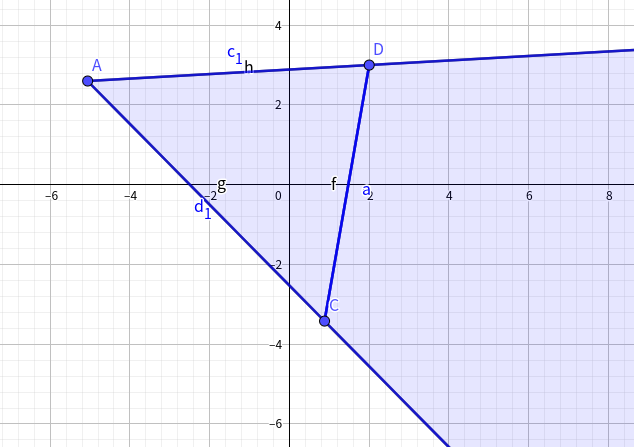
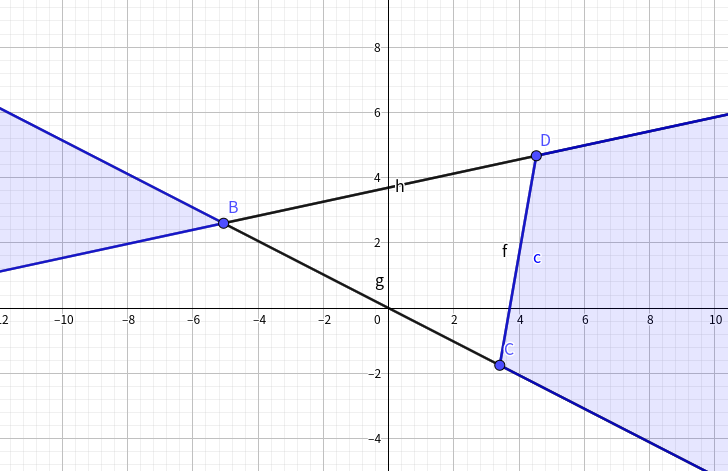
（务必注意\(\Delta BDC\)不能匹配）

这一些位置可以用以\(C,D\)作为直角坐标系中心点时的两段极角序区间的交描述，这样问题就变成了二维数点问题，对于每一个种族用线段树+二分进行二维数点即可。

这样可以过\(Q \leq 100\)的分数，对于更大的数据我们只需要在每一次询问的时候遍历攻击方和被攻击方中龙数量较少的一个，因为一组询问不会询问多于一次，所以不难证明这样做的复杂度是\(O(N^{1.5}logN)\)，就可以通过本题。

代码

LOJ2401 JOISC2017 Dragon2 计算几何、线段树的更多相关文章

  1. 【XSY3141】哲学家 计算几何 线段树

    题目描述 有一个平面,最开始平面上没有任何点. 你要按顺序加入 \(n\) 个点,求加入每个点后有多少三角形严格包含原点(在边界上不算). \(n\leq 400000\),无重点. 题解 其实这题本 ...

  2. 2019牛客多校第八场 F题 Flowers 计算几何+线段树

    2019牛客多校第八场 F题 Flowers 先枚举出三角形内部的点D. 下面所说的旋转没有指明逆时针还是顺时针则是指逆时针旋转. 固定内部点的答案的获取 anti(A)anti(A)anti(A)或 ...

  3. POJ 2991 Crane（线段树+计算几何）

    POJ 2991 Crane 题目链接 题意:给定一个垂直的挖掘机臂.有n段,如今每次操作能够旋转一个位置,把[s, s + 1]专程a度,每次旋转后要输出第n个位置的坐标 思路:线段树.把每一段当成 ...

  4. Codeforces Gym100543B 计算几何 凸包 线段树 二分/三分 卡常

    原文链接https://www.cnblogs.com/zhouzhendong/p/CF-Gym100543B.html 题目传送门 - CF-Gym100543B 题意 给定一个折线图,对于每一条 ...

  5. POJ 3667 Hotel(线段树 区间合并)

    Hotel 转载自:http://www.cnblogs.com/scau20110726/archive/2013/05/07/3065418.html [题目链接]Hotel [题目类型]线段树 ...

  6. 线段树(单标记+离散化+扫描线+双标记)+zkw线段树+权值线段树+主席树及一些例题

    “队列进出图上的方向 线段树区间修改求出总量 可持久留下的迹象 我们 俯身欣赏” ----<膜你抄>     线段树很早就会写了,但一直没有总结,所以偶尔重写又会懵逼,所以还是要总结一下. ...

  7. POJ 3667 线段树区间合并

    http://www.cnblogs.com/scau20110726/archive/2013/05/07/3065418.html 用线段树,首先要定义好线段树的节点信息,一般看到一个问题,很难很 ...

  8. 【BZOJ 3165】 [Heoi2013]Segment 李超线段树

    所谓李超线段树就是解决此题一类的问题(线段覆盖查询点最大(小)),把原本计算几何的题目变成了简单的线段树,巧妙地结合了线段树的标记永久化与标记下传,在不考虑精度误差的影响下,打法应该是这样的. #in ...

  9. poj 3667 Hotel （线段树的合并操作）

    Hotel The cows are journeying north to Thunder Bay in Canada to gain cultural enrichment and enjoy a ...

随机推荐

  1. nginx return配置说明

    该指令一般用于对请求的客户端直接返回响应状态码.在该作用域内return后面的所有nginx配置都是无效的. 可以使用在server.location以及if配置中. 除了支持跟状态码,还可以跟字符串 ...

  2. vue 百度地图多标注展示和点击标注进行的提示

    index.html中加入script <script type="text/javascript" src="http://api.map.baidu.com/a ...

  3. Kubernetes中如何让Deployment更新镜像

    问题描述 我的deployment有单个pod,我的自定义docker镜像如下: 123 containers: - name: mycontainer image: myimage:latest 在 ...

  4. attempt to call method 'getDataString' (a nil value)

    错误: LUA ERROR: [: attempt to call method 'getDataString' (a nil value) 在合并cocos和quick的时候,在EventCusto ...

  5. 转载：关于思科交换机、路由器如何关闭telnet 开启ssh服务

    等保测评要求: 必须关闭telnet服务,开启ssh服务 即用ssh方式登录网络设备,而不允许用telnet. 输入密码.en 再次输入密码.sh run 这些常规动作就不再赘述. 1.关闭telne ...

  6. 如何将 普通代码变成 java lamband表达式

    public static void main(String[] args) { Map<String, String> map = new HashMap<>(); List ...

  7. C# RSA 无 长度限制 加密解密 示例

    RSA 是一种非对称加密算法.由于算法特性,加密和解密过程用不同密钥,即公钥和私钥,而被广泛应用于数字证书的安全管理. 在具体应用中,公钥用加密而私钥用于解密,或 私钥用于数字签名而公钥用于签名验证. ...

  8. python-selenium登陆今日头条

    https://blog.csdn.net/a942242856/article/details/88379727 原文地址:http://www.bianbingdang.com/article_d ...

  9. RocketMQ、Kafka、RabbitMQ的对比

    RocketMQ 相比于 RabbitMQ.Kafka 具有主要优势特性有: 支持事务型消息(消息发送和DB操作保持两方的最终一致性,RabbitMQ 和Kafka 不支持) 支持结合 RocketM ...

  10. Raw image encoder error: Empty JPEG image (DNL not supported)) in throwOnEror

    OpenCV Error: Unknown error code -10 (Raw image encoder error: Empty JPEG image (DNL not supported)) ...