[LeetCode] 850. Rectangle Area II 矩形面积之二

We are given a list of (axis-aligned) `rectangles`.  Each `rectangle[i] = [x1, y1, x2, y2] `, where (x1, y1) are the coordinates of the bottom-left corner, and (x2, y2) are the coordinates of the top-right corner of the `i`th rectangle.

Find the total area covered by all rectangles in the plane.  Since the answer may be too large, return it modulo 10^9 + 7.

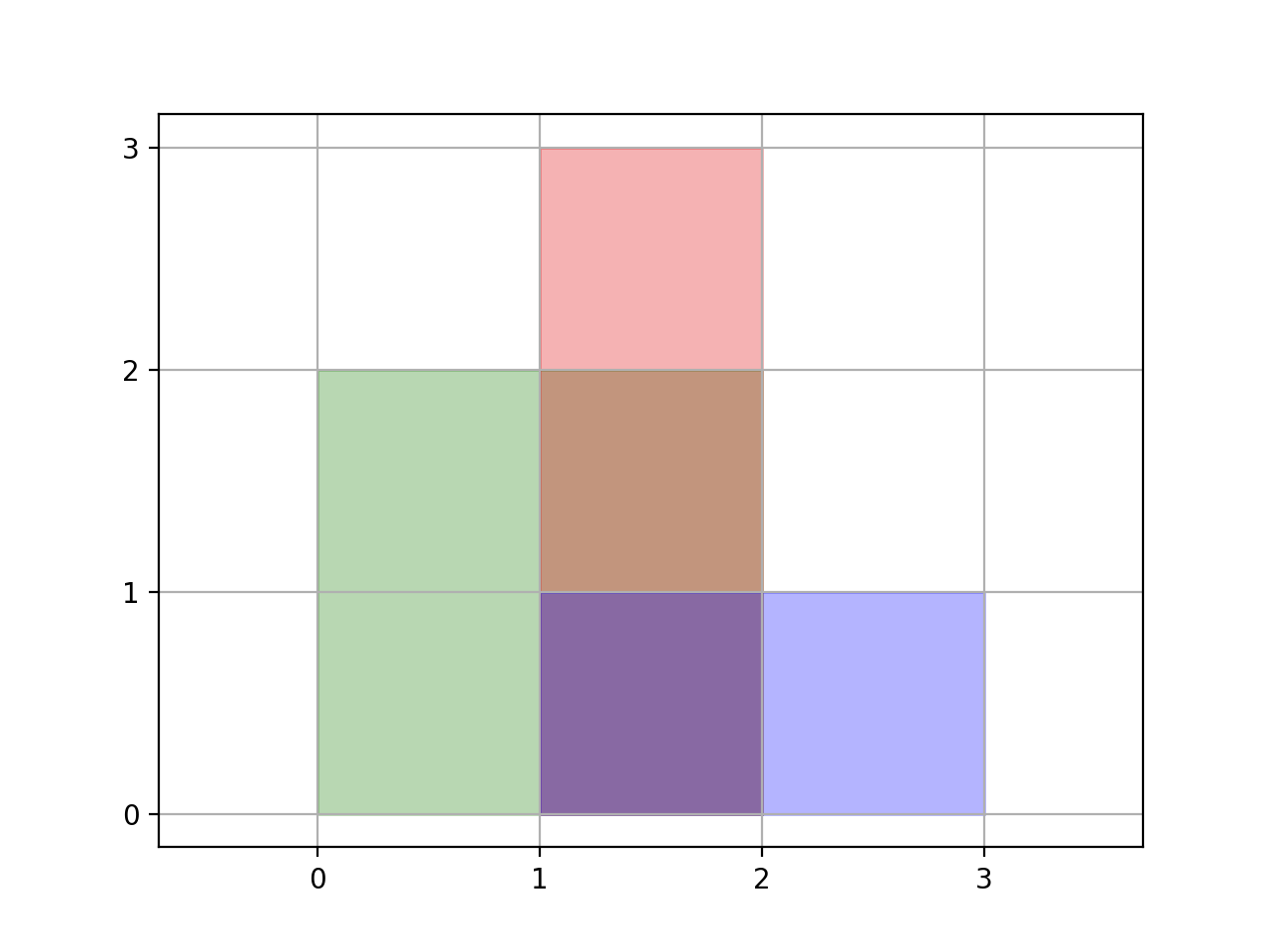
Example 1:

Input: [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
Output: 6
Explanation: As illustrated in the picture.

Example 2:

Input: [[0,0,1000000000,1000000000]]
Output: 49
Explanation: The answer is 10^18 modulo (10^9 + 7), which is (10^9)^2 = (-7)^2 = 49.

Note:

• 1 <= rectangles.length <= 200
• rectanges[i].length = 4
• 0 <= rectangles[i][j] <= 10^9
• The total area covered by all rectangles will never exceed 2^63 - 1 and thus will fit in a 64-bit signed integer.

这道题是之前那道 [Rectangle Area](http://www.cnblogs.com/grandyang/p/4563153.html) 的拓展，那道题只有两个矩形重叠，而这道题有多个矩形可能同时重叠，整体难度一下就上来了，那么通过将所有矩形面积加起来再减去重叠区域的方法这里就不太适用了，因为多个矩形在同一区域重叠的话，都减去重叠面积是会错的，还得把多减的补回来，相当的麻烦。这里我们需要换一种解题的思路，不能一股脑儿的把所有的矩形都加起来，而是应该利用微积分的思想，将重叠在一起的区域拆分成一个个的小矩形，分别累加面积，因为这里的矩形是不会旋转的，所以是可以正常拆分的。思路有了，新建一个二维数组 all 来保存所有的矩形，然后遍历给定的矩形数组，对于每个遍历到的数组，调用一个子函数，将当前的矩形加入 all 中。下面主要来看一下这个子函数 helper 该如何实现？首先要明白这个函数的作用是将当前矩形加入 all 数组中，而且用的是递归的思路，所以要传入一个 start 变量，表示当前和 all 数组中正在比较的矩形的 index，这样在开始的时候，检查一下若 start 大于等于 all 数组长度，表示已经检测完 all 中所有的矩形了，将当前矩形加入 all 数组，并返回即可。否则的话则取出 start 位置上的矩形 rec，此时就要判断当前要加入的矩形和这个 rec 矩形是否有重叠，这在 LeetCode 中有专门一道题是考察这个的 [Rectangle Overlap](https://www.cnblogs.com/grandyang/p/10367583.html)，这里用的就是那道题的判断方法，假如判断出当前矩形 cur 和矩形 rec 没有交集，就直接对 all 数组中下一个矩形调用递归函数，并返回即可。假如有重叠的话，就稍微麻烦一点，由于重叠的部位不同，所以需要分情况讨论一下，参见下图所示：

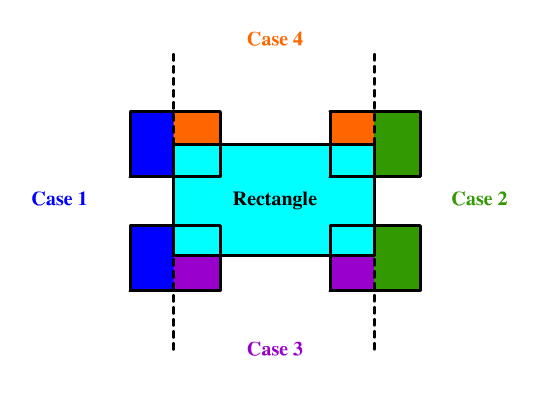
对于一个矩形 Rectangle，若有另外一个矩形跟它有重叠的话，可以将重叠区域分为四个部分，如上图的 Case1，Case2，Case3，Case4 所示，非重叠部分一定会落在一个或多个区域中，则可以把这些拆开的小矩形全部加入到矩形数组 all 中。仔细观察上图可以发现，对于将矩形 cur 拆分的情况可以分为下面四种：

• 落入区间1，条件为 cur[0] < rec[0]，产生的新矩形的两个顶点为 {cur[0], cur[1], rec[0], cur[3]}。
• 落入区间2，条件为 cur[2] > rec[2]，产生的新矩形的两个顶点为 {rec[2], cur[1], cur[2], cur[3]}。
• 落入区间3，条件为 cur[1] < rec[1]，产生的新矩形的两个顶点为 {max(rec[0], cur[0]), cur[1], min(rec[2], cur[2]), rec[1]}。
• 落入区间4，条件为 cur[3] > rec[3]，产生的新矩形的两个顶点为 {max(rec[0], cur[0]), rec[3], min(rec[2], cur[2]), cur[3]}。

这样操作下来的话，整个所有的区域都被拆分成了很多个小矩形，每个矩形之间都不会有重复，最后只要分别计算每个小矩形的面积，并累加起来就是最终的结果了，参见代码如下：

解法一：

class Solution {
public:
    int rectangleArea(vector<vector<int>>& rectangles) {
        long res = 0, M = 1e9 + 7;
        vector<vector<int>> all;
        for (auto rectangle : rectangles) {
            helper(all, rectangle, 0);
        }
        for (auto &a : all) {
            res = (res + (long)(a[2] - a[0]) * (long)(a[3] - a[1])) % M;
        }
        return res;
    }
    void helper(vector<vector<int>>& all, vector<int> cur, int start) {
        if (start >= all.size()) {
            all.push_back(cur); return;
        }
        auto rec = all[start];
        if (cur[2] <= rec[0] || cur[3] <= rec[1] || cur[0] >= rec[2] || cur[1] >= rec[3]) {
            helper(all, cur, start + 1); return;
        }
        if (cur[0] < rec[0]) {
            helper(all, {cur[0], cur[1], rec[0], cur[3]}, start + 1);
        }
        if (cur[2] > rec[2]) {
            helper(all, {rec[2], cur[1], cur[2], cur[3]}, start + 1);
        }
        if (cur[1] < rec[1]) {
            helper(all, {max(rec[0], cur[0]), cur[1], min(rec[2], cur[2]), rec[1]}, start + 1);
        }
        if (cur[3] > rec[3]) {
            helper(all, {max(rec[0], cur[0]), rec[3], min(rec[2], cur[2]), cur[3]}, start + 1);
        }
    }
};

下面这种解法更是利用了微积分的原理，把x轴长度为1当作一个步长，然后计算每一列有多少个连续的区间，每个连续区间又有多少个小正方形，题目中给的例子每一个列都只有一个连续区间，但事实上是可以有很多个的，只要算出了每一列 1x1 小正方形的个数，将所有列都累加起来，就是整个区域的面积。这里求每列上小正方形个数的方法非常的 tricky，博主也不知道该怎么讲解，大致就是要求同一列上每个连续区间中的小正方形个数，再累加起来。对于每个矩形起始的横坐标，映射较低的y值到1，较高的y值到 -1，对于结束位置的横坐标，刚好反过来一下，映射较低的y值到 -1，较高的y值到1。这种机制跟之前那道 [The Skyline Problem](http://www.cnblogs.com/grandyang/p/4534586.html) 有些异曲同工之妙，都还是为了计算高度差服务的。要搞清楚这道题的核心思想，不是一件容易的事，博主的建议是就拿题目中给的例子带入到下面的代码中，一步一步执行，并分析结果，是能够初步的了解解题思路的，若实在有理解上的问题，博主可以进一步写些讲解，参见代码如下：


解法二：

class Solution {
public:
    int rectangleArea(vector<vector<int>>& rectangles) {
        long res = 0, pre_x = 0, height = 0, start = 0, cnt = 0, M = 1e9 + 7;
        map<int, vector<pair<int, int>>> groupMap;
        map<int, int> cntMap;
        for (auto &a : rectangles) {
        	groupMap[a[0]].push_back({a[1], 1});
        	groupMap[a[0]].push_back({a[3], -1});
        	groupMap[a[2]].push_back({a[1], -1});
        	groupMap[a[2]].push_back({a[3], 1});
        }
        for (auto &group : groupMap) {
        	res = (res + (group.first - pre_x) * height) % M;
        	for (auto &a : group.second) {
        		cntMap[a.first] += a.second;
        	}
        	height = 0, start = 0, cnt = 0;
        	for (auto &a : cntMap) {
        		if (cnt == 0) start = a.first;
        		cnt += a.second;
        		if (cnt == 0) height += a.first - start;
        	}
        	pre_x = group.first;
        }
        return res;
    }
};

Github 同步地址:

https://github.com/grandyang/leetcode/issues/850

类似题目：

Rectangle Overlap

Rectangle Area

The Skyline Problem

参考资料：

https://leetcode.com/problems/rectangle-area-ii/

https://leetcode.com/problems/rectangle-area-ii/discuss/138028/Clean-Recursive-Solution-Java

https://leetcode.com/problems/rectangle-area-ii/discuss/214365/Short-C%2B%2B-solution.-EZ-to-understand.-Beat-99.

[LeetCode All in One 题目讲解汇总(持续更新中...)](https://www.cnblogs.com/grandyang/p/4606334.html)