原创：logistic regression实战（一）：SGD Without lasso

　　logistic regression是分类算法中非常重要的算法，也是非常基础的算法。logistic regression从整体上考虑样本预测的精度，用判别学习模型的条件似然进行参数估计，假设样本遵循iid,参数估计时保证每个样本的预测值接近真实值的概率最大化。这样的结果，只能是牺牲一部分的精度来换取另一部分的精度。而svm从局部出发，假设有一个分类平面，找出所有距离分类平面的最近的点(support vector,数量很少)，让这些点到平面的距离最大化，那么这个分类平面就是最佳分类平面。从这个角度来看待两个算法，可以得出logistic regression的精度肯定要低于后者。今天主要写logistic regression的Python代码。logistic regression的推导过程比较简单：

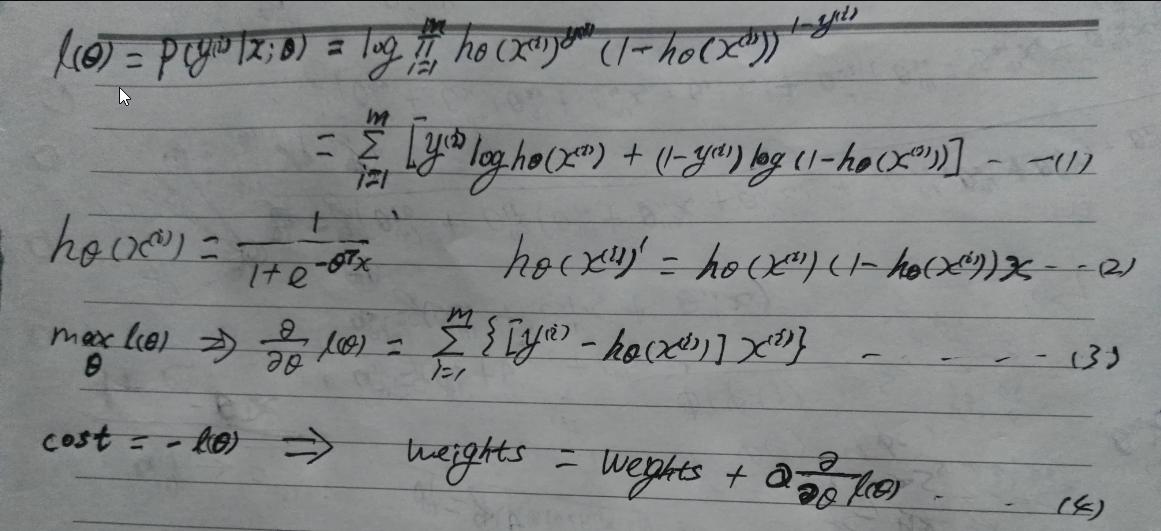
　　第一个公式是条件似然函数估计，意思是指定未知常量theta（;表示频率学派），对于每个输入feature vector x(i),产生y(i)的概率都最大，取对数是为了求导方便。第二个公式是sigmoid函数的导数，在这里推导出具体的导函数(推导过程非常简单，复合函数求导法则)，第三个公式是求出的梯度(实际为偏导数组成的向量，梯度与方向导数同方向时取得最大值，相反时取得最小值)。公式3的线性意义为：对于容量为m的样本(矩阵mxn),权重为nx1的列向量，每一行的样本数据与权重向量相乘求得预测值，m行样本的预测值组成mx1的列向量(其数值为exp（-inX）)，其实就是mxn的样本矩阵左乘权重向量nx1，因为的矩阵的本质是线性变换，相当于每一行样本数据投影到权重向量。得到预测值的列向量后，与真实值向量(需要转置）做差值得到新的列向量。最后样本矩阵倒置，然后左乘这个向量得到nx1的权重向量(梯度)。这个过程是计算批量梯度。当似然函数取得最大时，就是损失函数最小，所以二者是相反的关系，最后结果也就是梯度上升法。

　　对于逻辑回归的损失函数，也可以从另外一个角度来理解。上面的公式我们看到损失函数和最大似然函数是相反的关系，一般情况下，logistic regression的loss function 可以采用交叉熵的形式，然后取mean。

　　SGD(stochastic gradient descent)在计算的过程中，每次迭代不用计算所用样本，而是随机选取一个样本进行梯度上升(下降)，在工程实践中可以满足精度要求，而且时间复杂度比批量要低。对于SGD而言，学习速率alpha的选取，随着循环次数增加，刚开始的时候，梯度下降应该比较快，到后期的时候，可能会出现在某一个值徘徊的情况，而且下降速率会越来越慢。所以选取一个比较合理的study rate,应该是先选取到的样本study rate相对较高，后面的相对较小，这样比较合理。

　　在训练出模型后，预测时应该使用"五折交叉验证理论"寻找出最优模型出来(调节参数的过程)，这个过程一般用RMSE（均方根误差）来衡量，并且可以定义一个基准均方根误差。在用最优模型预测时取得的RMSE与基准RMSE对比，分析数据结果。

　　本文主要探讨logistic regression的SGD算法，并且不考虑正则化。事实上，在高维度的情况下，泛化能力或者正则化技术非常关键。在90年代有学者提出lasso后，至今有很多方法实践了lasso,比如LARS，CD……。下一篇博客将探讨lasso技术，并且动手实践CD算法。接下来，上传最近写的SGD Python代码,首先是引入模块：logisticRegression.py，这里面定义了两个class:LogisticRegressionWithSGD,LRModel,还有全局函数RMSE，loadDataSet和sigmoid函数。后面是测试代码，主要是参数调优。

logisticRegression.py：

 '''
 Created on 2017/03/15
 Logistic Regression without lasso
 @author: XueQiang Tong
 '''
 '''
 this algorithm include SGD，batch gradient descent except lasso regularization，So the generalization
 ability is relatively weak, follow-up and then write a CD algorithm for lasso.
 '''
 from numpy import *
 import matplotlib.pyplot as plt
 import numpy as np;

 # load dataset into ndarray(numpy)
 def loadDataSet(filepath, seperator="\t"):
     with open(filepath) as fr:
         lines = fr.readlines();
         num_samples = len(lines);
         dimension = len(lines[0].strip().split(seperator));
         dataMat = np.zeros((num_samples, dimension));
         labelMat = [];

     index = 0;
     for line in lines:
         sample = line.strip().split();
         feature = list(map(np.float32, sample[:-1]));
         dataMat[index, 1:] = feature;
         dataMat[index, 0] = 1.0;
         labelMat.append(float(sample[-1]));
         index += 1;

     return dataMat, array(labelMat);

 #sigmoid function
 def sigmoid(inX):
     return 1.0/(1+exp(-inX))

 # compute rmse
 def RMSE(true,predict):
     true_predict = zip(true,predict);
     sub = [];
     for r,p in true_predict:
         sub.append(math.pow((r-p),2));
     return math.sqrt(mean(sub));

 def maxstep(dataMat):
     return 2 / abs(np.linalg.det(np.dot(dataMat.transpose(),dataMat)));

 class LRModel:
     def __init__(self,weights = np.empty(10),alpha = 0.01,iter = 150):
         self.weights = weights;
         self.alpha = alpha;
         self.iter = iter;

     #predict
     def predict(self,inX):
         prob = sigmoid(dot(inX,self.weights))
         if prob > 0.5: return 1.0
         else: return 0.0

     def getWeights(self):
         return self.weights;

     def __getattr__(self, item):
         if item == 'weights':
             return self.weights;

 class LogisticRegressionWithSGD:
     # batch gradient descent
     @classmethod
     def batchGradDescent(cls,data,maxCycles = 500,alpha = 0.001):
         dataMatrix = mat(data[0])             # convert to NumPy matrix
         labelMat = mat(data[1]).transpose() # convert to NumPy matrix
         m,n = shape(dataMatrix)
         weights = ones((n,1))
         for k in range(maxCycles):
             h = sigmoid(dataMatrix*weights)    # compute predict_value
             error = (labelMat - h)              # compute deviation
             weights = weights + alpha * dataMatrix.transpose()* error # update weight

         model = LRModel(weights = weights,alpha = alpha,iter = maxCycles);
         return model;

     '''
     # draw samples of the scatter plot to view the distribution of sample points
     @classmethod
     def viewScatterPlot(cls,weights,dataMat,labelMat):
         dataArr = array(dataMat)
         n = shape(dataArr)[0]
         xcord1 = []; ycord1 = []
         xcord2 = []; ycord2 = []
         for i in range(n):
             if int(labelMat[i])== 1:
                 xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
             else:
                 xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
         fig = plt.figure()
         ax = fig.add_subplot(111)
         ax.scatter(xcord1, ycord1, s=30, c='red', marker='s',label='1')
         ax.scatter(xcord2, ycord2, s=30, c='green',label='0')
         plt.legend();
         x = arange(-3.0, 3.0, 0.1)
         y = (-weights[0]-weights[1]*x)/weights[2]
         ax.plot(mat(x), mat(y))
         plt.xlabel('X1'); plt.ylabel('X2');
         plt.show()
     '''
     @classmethod
     def train_nonrandom(cls,data,alpha = 0.01):
         dataMatrix = data[0];
         classLabels = data[1];
         m,n = shape(dataMatrix);
         weights = ones(n)   #initialize to all ones
         for i in range(m):
             h = sigmoid(sum(dataMatrix[i]*weights));
             error = classLabels[i] - h;
             weights = weights + alpha * error * dataMatrix[i];

         model = LRModel(weights = weights,alpha = alpha);
         return model;

     @classmethod
     def train_random(cls,data, numIter=150):
         dataMatrix = data[0];
         classLabels = data[1];
         m,n = shape(dataMatrix);
         weights = ones(n);   #initialize to all ones
         indices = np.arange(len(dataMatrix))
         for iter in range(numIter):
             np.random.shuffle(indices)
             for index in indices:
                 alpha = 4 / (1.0 + iter + index) + 0.0001    #apha decreases with iteration, does not
                 h = sigmoid(sum(dataMatrix[index]*weights));
                 error = classLabels[index] - h;
                 weights = weights + alpha * error * array(dataMatrix[index]);

         model = LRModel(weights = weights,iter = numIter);
         return model;

     def colicTest(self):
         data = loadDataSet('G:\\testSet.txt');
         trainWeights = self.stoGradDescent_random(data);
         dataMat = data[0];
         labels = data[1];
         errnums = 0;
         for index in range(dataMat.shape[0]):
             preVal = self.predict(dataMat[index,:],trainWeights);
             if(preVal != labels[index]):
                 errnums += 1;
         print('error rate:%.2f' % (errnums/dataMat.shape[0]));
         return errnums;

     def multiTest(self):
         numTests = 10; errorSum=0.0
         for k in range(numTests):
             errorSum += self.colicTest()
         print("after %d iterations the average error rate is: %.2f" % (numTests, errorSum/numTests))

测试代码，把最优模型保存在npy文件里，以后使用的时候，直接取出来，不用再训练了。

 from logisticRegression import *;
 from numpy import *;
 import math;

 def main():
     dataMat, labels = loadDataSet('G:\\testSet.txt');
     num_samples = dataMat.shape[0];

     num_trains = int(num_samples * 0.6);
     num_validations = int(num_samples * 0.2);
     num_tests = int(num_samples * 0.2);

     data_trains = dataMat[:num_trains, :];
     data_validations = dataMat[num_trains:(num_trains + num_validations), :];
     data_tests = dataMat[(num_trains + num_validations):, :];

     label_trains = labels[:num_trains];
     label_validations = labels[num_trains:(num_trains + num_validations)];
     label_tests = labels[(num_trains + num_validations):];
     '''
     minrmse = (1 << 31) - 1;
     bestModel = LRModel();
     iterList = [10, 20, 30, 80];

     for iter in iterList:
         model = LogisticRegressionWithSGD.train_random((data_trains, label_trains), numIter=iter);
         preVals = zeros(num_validations);
         for i in range(num_validations):
             preVals[i] = model.predict(data_validations[i, :]);

         rmse = RMSE(label_validations, preVals);
         if rmse < minrmse:
             minrmse = rmse;
             bestModel = model;

     print(bestModel.iter, bestModel.weights, minrmse);
     save('D:\\Python\\models\\weights.npy',bestModel.weights);'''

     #用最佳模型预测测试集的评分，并计算和实际评分之间的均方根误差
     weights = load('D:\\Python\\models\\weights.npy');

     LogisticRegressionWithSGD.viewScatterPlot(weights,dataMat,labels);#显示散点图
     model = LRModel();
     model.weights = weights;

     preVals = zeros(num_tests);
     for i in range(num_tests):
         preVals[i] = model.predict(data_tests[i,:]);

     testRMSE = RMSE(label_tests,preVals); #预测产生的均方根误差
     #用基准偏差衡量最佳模型在测试数据上的预测精度
     tavMean = mean(hstack((label_trains,label_validations)));
     baseRMSE = math.sqrt(mean((label_tests - tavMean) ** 2)) #基准均方根误差

     improvement = abs(testRMSE - baseRMSE) / baseRMSE * 100;

     print("The best model improves the base line by %% %1.2f" % (improvement));

 if __name__ == '__main__':
     main();

运行结果：
样本点的散点图：

最佳迭代次数，权重以及RMSE：     10 [ 12.08509707   1.4723024   -1.86595103] 0.0
The best model improves the base line by % 55.07

另外，由于训练过程中是随机选取样本点，所以迭代次数相同的情况下，权重以及RMSE有可能不同，我们要的是RMSE最小的模型！
算法比较简单，但是用Python的nump库实施的时候，有很多注意的细节，只有经过自己仔细的理论推导然后再代码实施后，才能算基本掌握了一个算法。写代码及优化的过程是很费时的，后续还要改进算法，深化理论研究，并且坚持理论与编程结合，切不可眼高手低！