矩阵指数 Matrix Exponentials
转自:https://zh.wikipedia.org/wiki/%E7%9F%A9%E9%98%B5%E6%8C%87%E6%95%B0
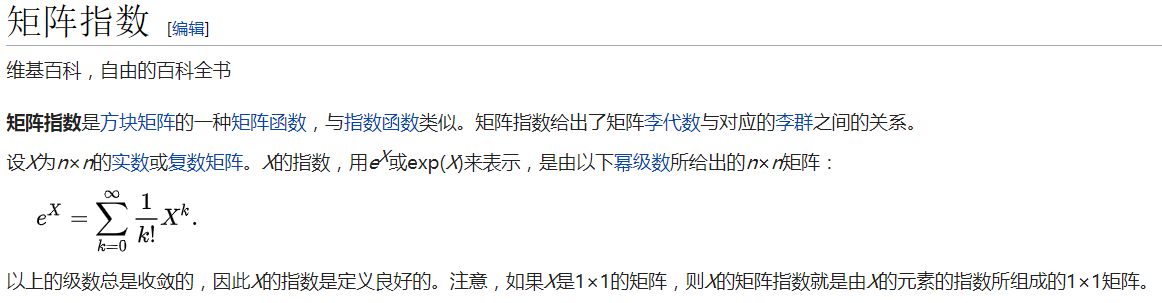
其中,X、 X2、X3……、Xk 都是n阶矩阵,显然 exp(X) 也为n阶矩阵,幂级数展开一定是收敛的,故 exp(X) 虽然不便手算出具体数值,但的确是一种解析表达;

矩阵指数在解ode中的作用:
实际是变量可分离的ode,通过分离变量求解,并表示为矩阵指数的形式

矩阵指数的解析解计算是数学研究中的一个讨论的要点,目前仅针对有特殊性质/形式矩阵有成熟的解法;
可以使用MATLAB expm()、logm() 函数进行近似计算

矩阵指数 Matrix Exponentials的更多相关文章
- R语言编程艺术# 矩阵(matrix)和数组(array)
矩阵(matrix)是一种特殊的向量,包含两个附加的属性:行数和列数.所以矩阵也是和向量一样,有模式(数据类型)的概念.(但反过来,向量却不能看作是只有一列或一行的矩阵. 数组(array)是R里更一 ...
- 【Math for ML】矩阵分解(Matrix Decompositions) (下)
[Math for ML]矩阵分解(Matrix Decompositions) (上) I. 奇异值分解(Singular Value Decomposition) 1. 定义 Singular V ...
- 【Math for ML】矩阵分解(Matrix Decompositions) (上)
I. 行列式(Determinants)和迹(Trace) 1. 行列式(Determinants) 为避免和绝对值符号混淆,本文一般使用\(det(A)\)来表示矩阵\(A\)的行列式.另外这里的\ ...
- R语言编程艺术#02#矩阵(matrix)和数组(array)
矩阵(matrix)是一种特殊的向量,包含两个附加的属性:行数和列数.所以矩阵也是和向量一样,有模式(数据类型)的概念.(但反过来,向量却不能看作是只有一列或一行的矩阵. 数组(array)是R里更一 ...
- NumPy 矩阵库(Matrix)
NumPy 矩阵库(Matrix) NumPy 中包含了一个矩阵库 numpy.matlib,该模块中的函数返回的是一个矩阵,而不是 ndarray 对象. 一个 的矩阵是一个由行(row)列(col ...
- 【线性代数】7-2:线性变化的矩阵(The Matrix of a Linear Transformation)
title: [线性代数]7-2:线性变化的矩阵(The Matrix of a Linear Transformation) categories: Mathematic Linear Algebr ...
- 【线性代数】2-4:矩阵操作(Matrix Operations)
title: [线性代数]2-4:矩阵操作(Matrix Operations) toc: true categories: Mathematic Linear Algebra date: 2017- ...
- 18、NumPy——矩阵库(Matrix)
NumPy 矩阵库(Matrix) NumPy 中包含了一个矩阵库 numpy.matlib,该模块中的函数返回的是一个矩阵,而不是 ndarray 对象. 一个 的矩阵是一个由行(row)列(col ...
- 从零开始学习R语言(三)——数据结构之“矩阵(Matrix)”
本文首发于知乎专栏:https://zhuanlan.zhihu.com/p/60140022 也同步更新于我的个人博客:https://www.nickwu.cn/blog/id=129 3. [二 ...
随机推荐
- EasyDSS高性能RTMP、HLS(m3u8)、HTTP-FLV、RTSP流媒体服务器软件实现的多码率视频点播功能说明
关于EasyDSS EasyDSS(http://www.easydss.com)流媒体解决方案采用业界优秀的流媒体框架模式设计,服务运行轻量.高效.稳定.可靠.易维护,支持RTMP直播.RTMP推送 ...
- LeetCode_463. Island Perimeter
463. Island Perimeter Easy You are given a map in form of a two-dimensional integer grid where 1 rep ...
- hashMap的原理
hashMap的原理分析(转载) 1.总结: HashMap是基于哈希表实现的,用Entry[]来存储数据,而Entry中封装了key.value.hash以及Entry类型的next HashMap ...
- 破解MySQL登录密码的几种方法
工具列表 Medusa Ncrack Hydra Metasploit Medusa medusa -h 192.168.1.106 –U /root/Desktop/user.txt –P /ro ...
- JobStorage.Current property value has not been initialized. You must set it before using Hangfire Client or Server API.
JobStorage.Current property value has not been initialized. You must set it before using Hangfire Cl ...
- Xcode7.2真机测试问题"The account 'appleID ' has no team with ID ‘’
在Xcode7(测试版)提出免费真机测试的时候,我立刻在网上搜寻测试步骤,很简单,按照步骤走就可以. 但在7.2以后,突然我的iPhone不能真调了!提示"The account 'app ...
- 【Spring Boot学习之十二】mybatis3 分页打印sql日志
环境 eclipse 4.7 jdk 1.8 Spring Boot 1.5.2 参考: mybatis手册 Mybatis的插件 PageHelper 分页查询使用方法MyBatis中Like语句使 ...
- 【视频开发】用GStreamer实现摄像头的采集和保存
GStreamer是流媒体软件的开发框架.可以这样说,在该框架的支持下,你可以非常简单地为很多格式的流媒体写出自已需要的程序. 现在,GStreamer已经内置对MP3.Ogg/Vorbis.MPEG ...
- SQL Server日志处理及安全访问
1.点SQL SERVER错误日志,右键,配置,限定错误日志的数目,比如6个 限制日志增长数量 2.然后运行命令: EXEC sp_cycle_errorlog ; 这个命令的作用是将当前日志归档,然 ...
- golang开发:环境篇(六) Go运行监控Supervisord的使用
为什么要使用Supervisord 17年第一次写Go项目的时候,用Go开发项目倒没没费多大劲,很快就开发完成了.到了在测试环境部署的时候,由于不知道有 Supervisord 这个软件,着实花了些功 ...
