GAN与VAE

经典算法·GAN与VAE

Generative Adversarial Networks 及其变体

生成对抗网络是近几年最为经典的生成模型的代表工作，Goodfellow的经典工作。通过两个神经网络结构之间的最大最小的博弈游戏然后生成模型。下面是原始GAN与一些GAN的变体。

Generative Adversarial Nets（GAN）

模型判别模块与生成模块的损失的定义：

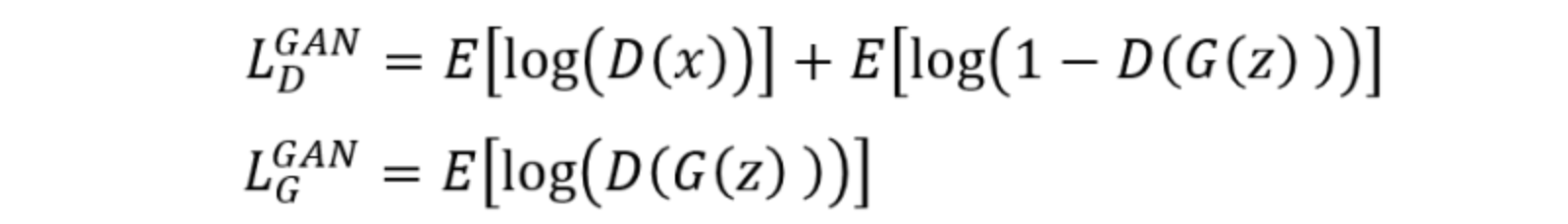
网络结构是：

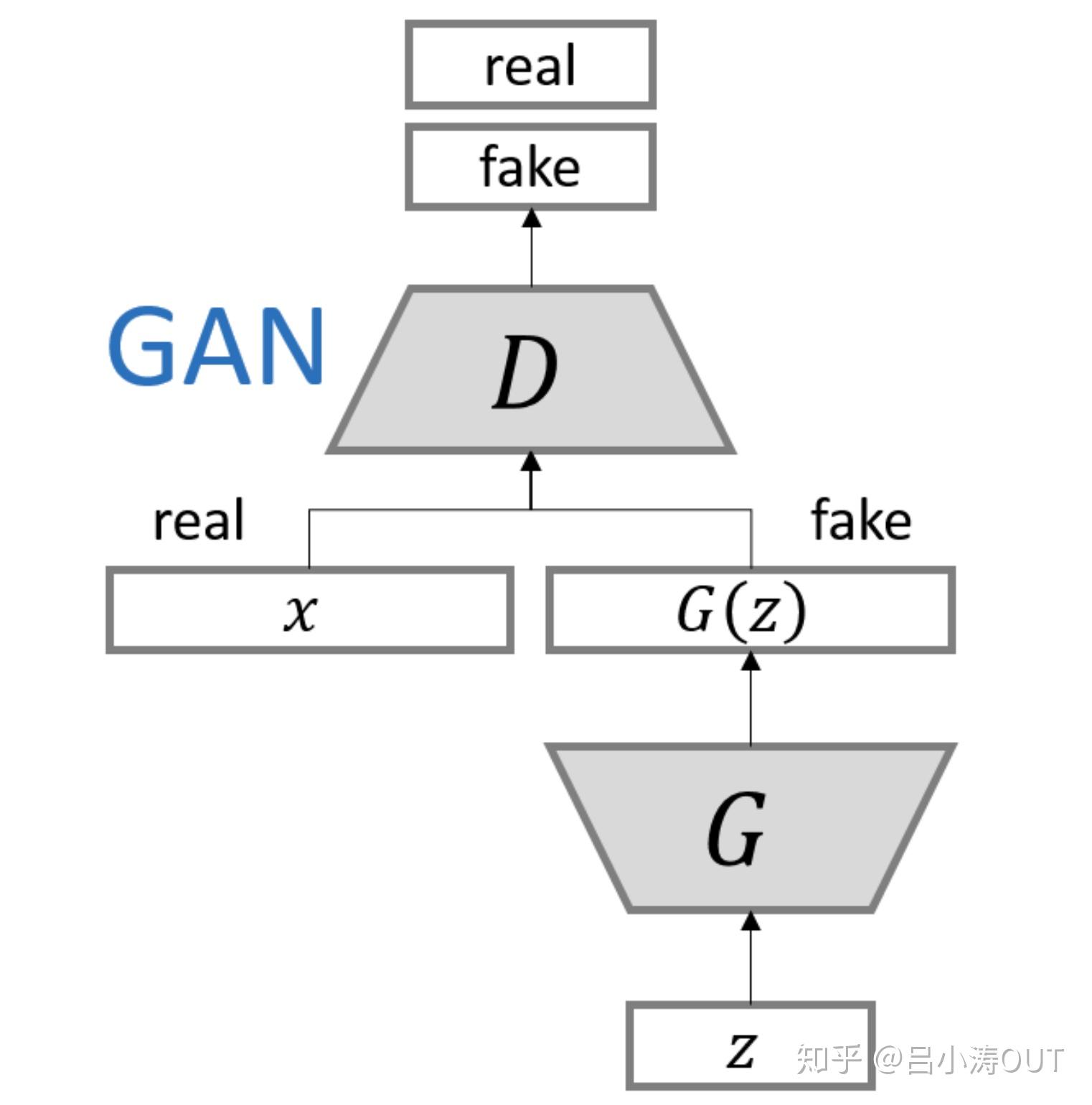
该结构的最大的问题有两个：一个是难以训练，一个是模型输出图片单调（model collapse）。

Conditional Generative Adversarial Nets（CGAN）

模型判别模块与生成模块的损失的定义：

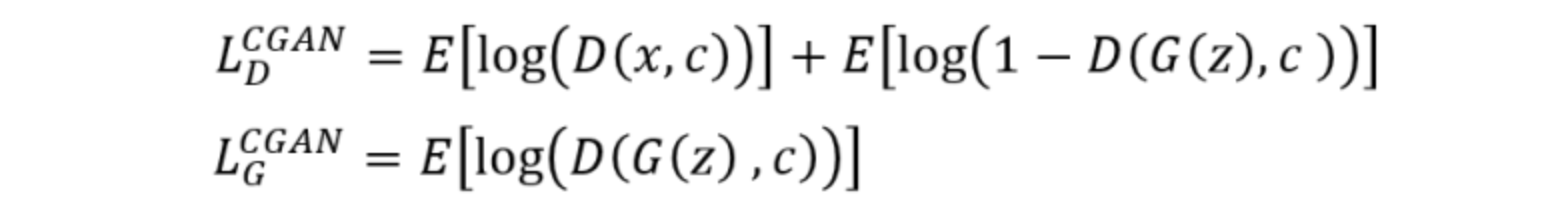
该模型结构如下图所示。与原始的网络结构的最大的变化便是增加了条件向量。

Wasserstein GAN（WGAN）

该论文是对GAN之前提到的问题的分析，结构上并没有具体的变化。通过调整损失函数来实现训练稳定与抑制model collapse。

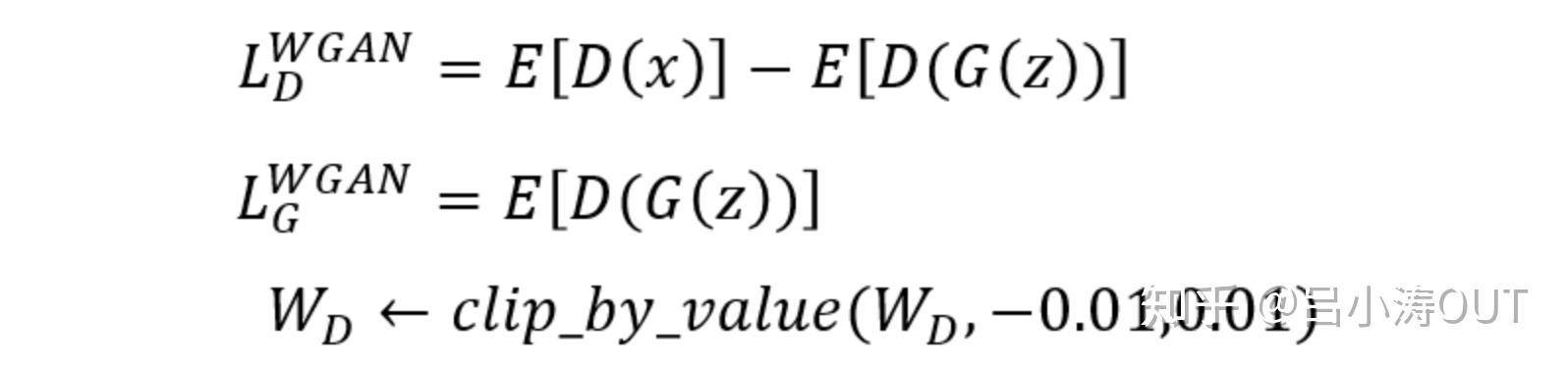
其中对参数的截断操作是因为Wasserstein距离中的近似计算中的条件约束导致的。

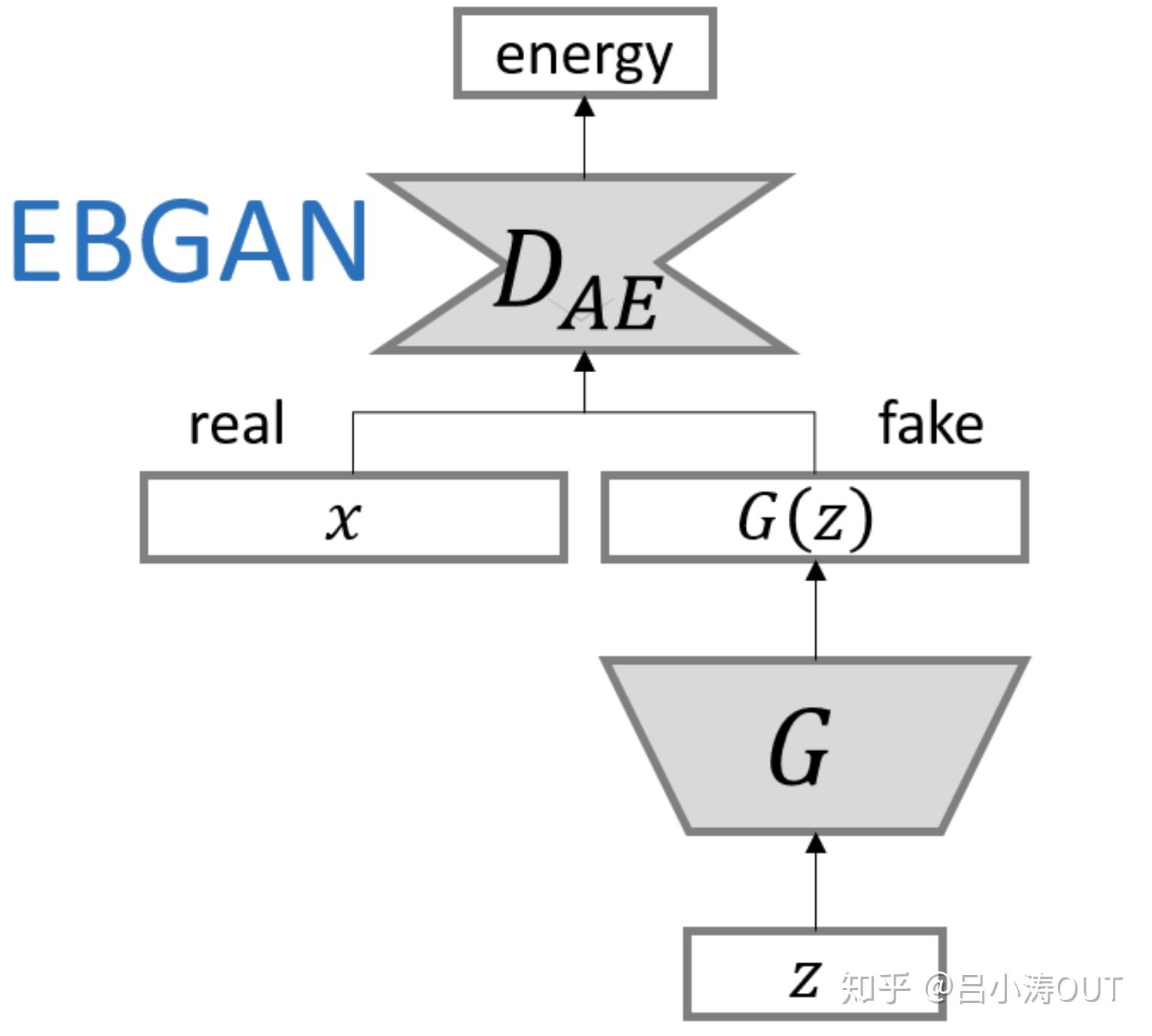
Energy-based Generative Adversarial Network（EBGAN）

原始的GAN的辨别模块是简单的神经网络。这里使用基于能量的神经网络进行真实样本与虚假样本分布的距离衡量。EBGAN的判别器是一个自编码器。那么EBGAN就是将判别器的输入输出求一个重构误差（rescontruction error），也就是判别器的输出，也即所说的能量（energy）。

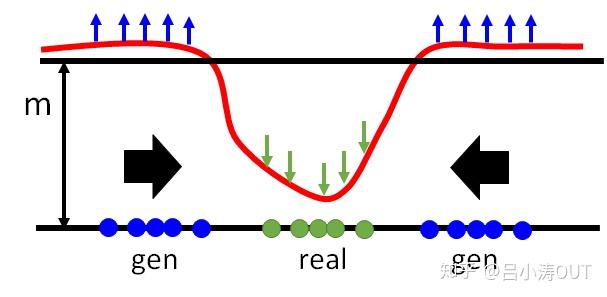
我们希望对于真实样本的重建误差小，同时希望由生成器生成的图片的能量小。那么D的损失函数中要最小化 -D(G(z)），就是最大化D(G(z))， 也就是要抬高下图中的蓝色点对应的曲线，但是如果没有margin的约束，可以无限制的抬高，所以我们需要一个m，即margin，就是当抬高到m这个距离后就没有惩罚了，所以此时loss就将不再忙着抬高，而是去将real对应的曲线也即D(x)拉小。generator做的事情就很好理解了，因为real对应的energy是小的，所以希望生成的图片的energy也是小的。

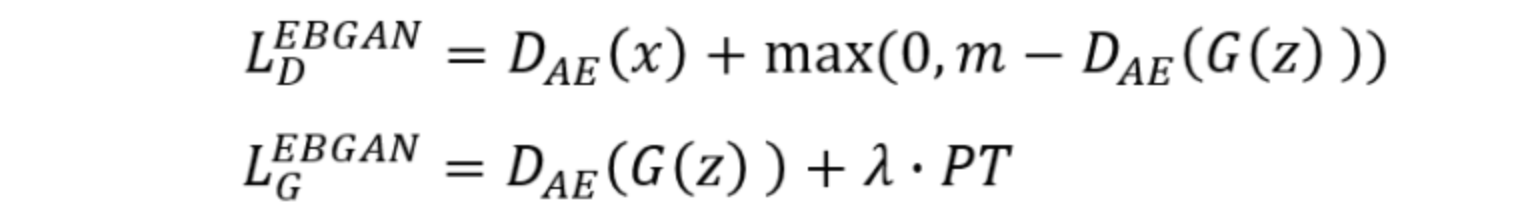
其中PT是编码后的结果的余弦相似度。网络结构如下图：

Auxiliary Classifier GANs（ACGAN）

ACGAN模型与CGAN类似。生成器都是输入类标签  和噪声  。在判别模块中不再输入类标签，另外在输入样本是否为真的同时，利用另一个分类器来判断输入样本的所属类别。

网络结构就是在条件GAN上加入了类别标签。

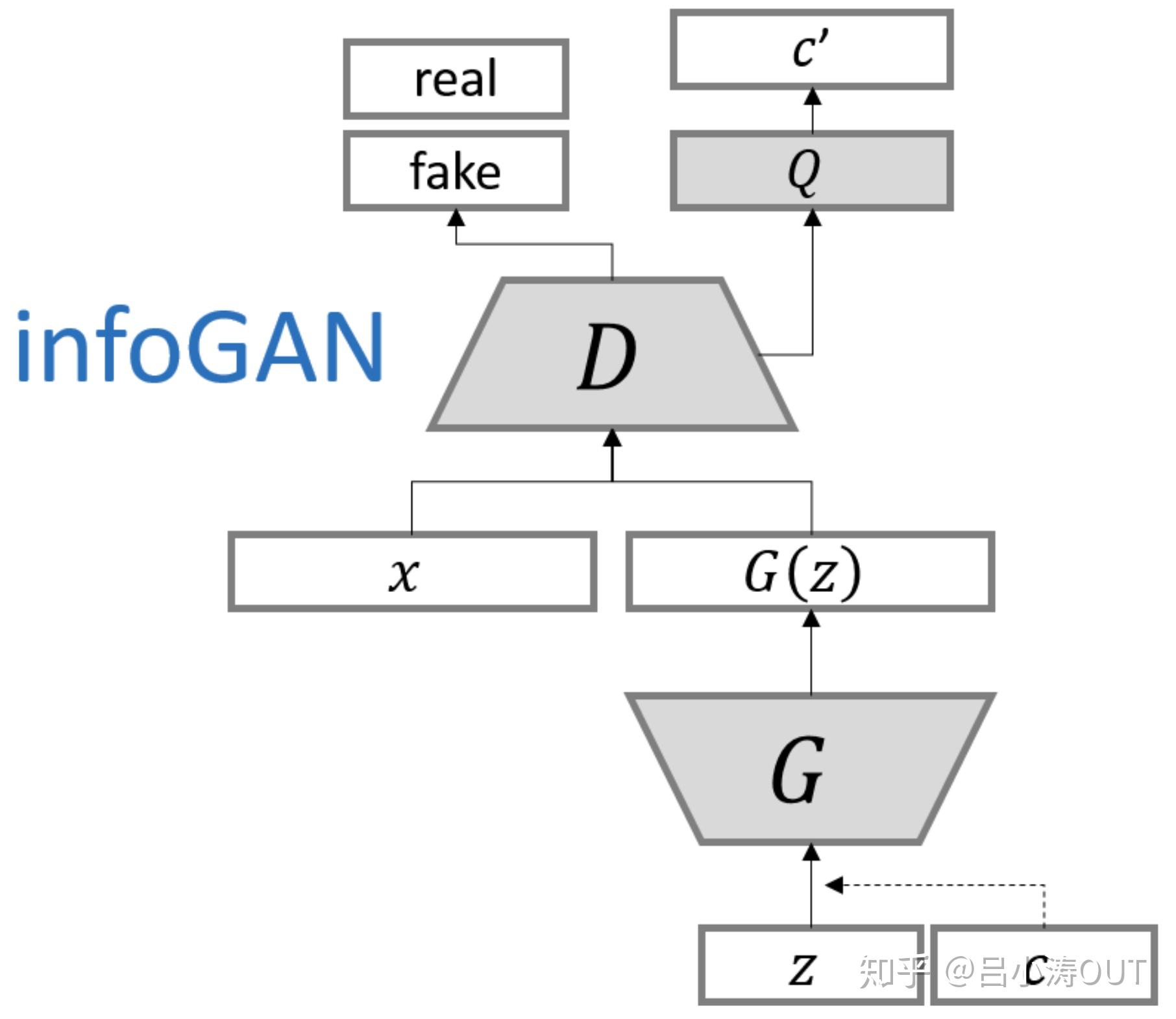
Information Maximizing Generative Adversarial Nets（InfoGAN）

模型将噪声拆分成两个部分，一部分是噪声信号，另一部分就是潜在信息。

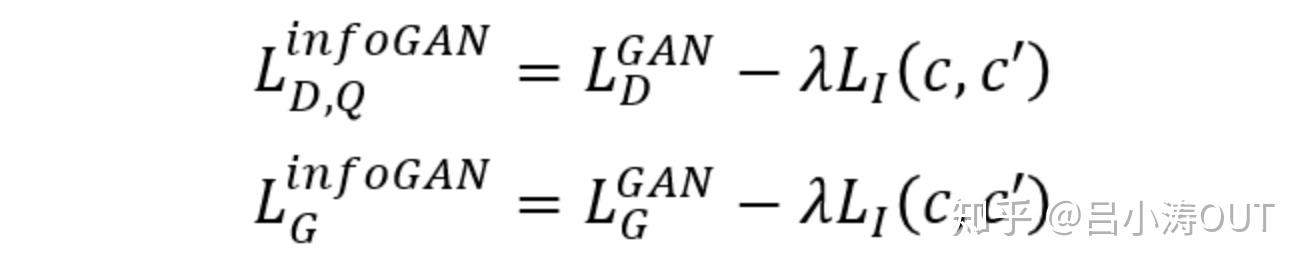
网络结构如图：

Variational Auto-Encoders 及其变体

通过编码过程生成目标分布的均值与方差，然后通过采样的技巧来复原目标样本分布，并且使用复原的分布和真实分布的距离来进行参数的调节。

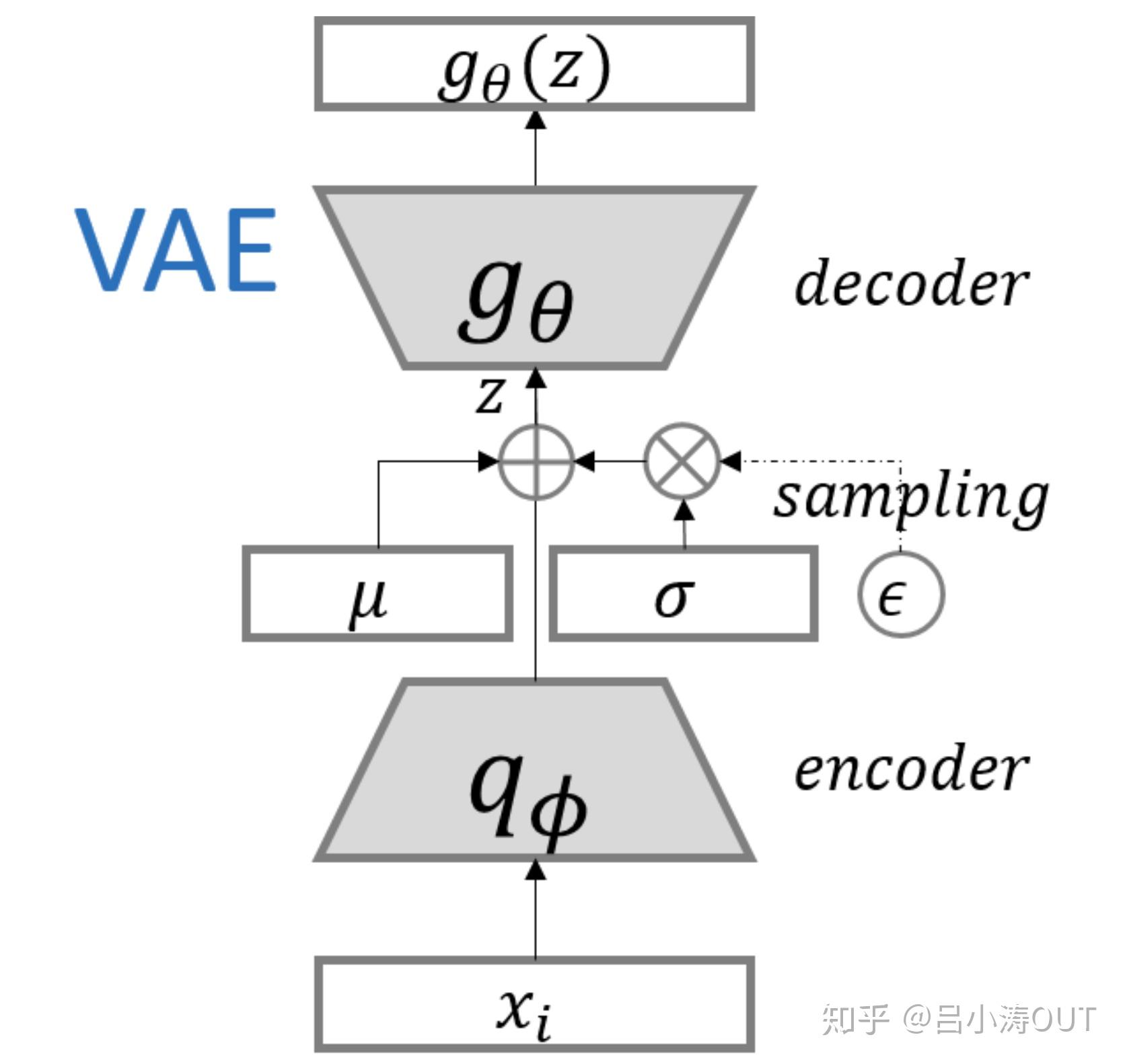
Variational Auto-Encoders（VAE）

变分自编码器的经典形式与网络结构：

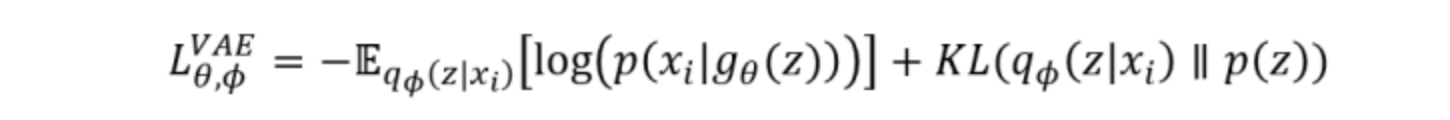
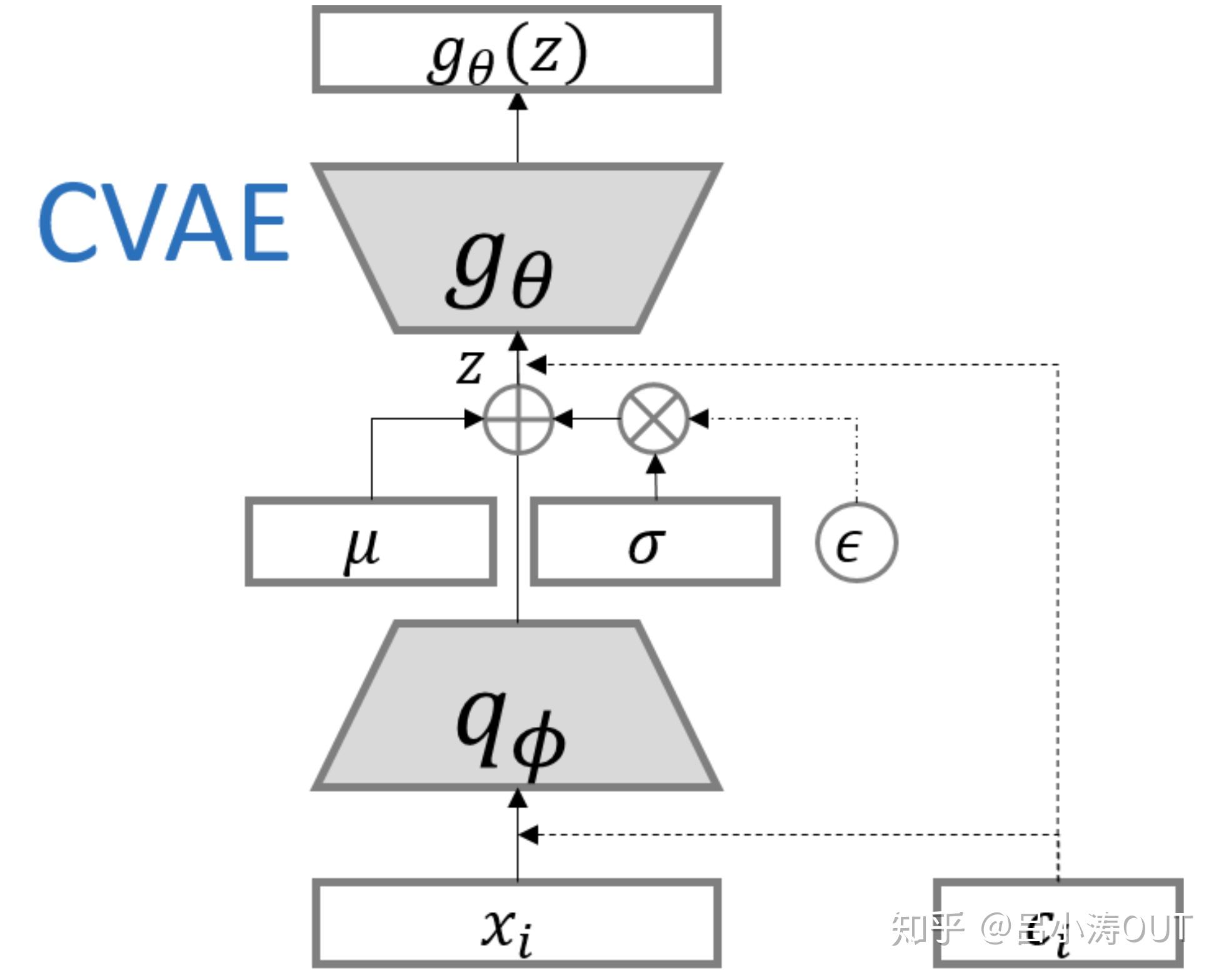
Conditional Variational Auto-Encoders（CVAE）

条件自编码器的构建和CGAN的构建是类似的。

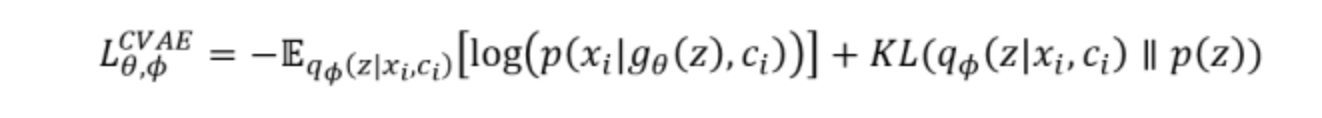
GAN与VAE的异同

1. GAN与VAE两个生成模型的Loss推导都可以放在联合概率密度的KL散度的统一框架下进行讨论，而且都得到了与原始推导相同的结果。
2. GAN与VAE所设计的隐变量不同，结构不同，导致了近似处理的方法不同，但它们的出发点是相同的（上述第一点）。
3. GAN最后的Loss反映的是生成样本与真实样本的概率流型之间的距离，而VAE最后的Loss反映的是Auto-Encoder的输出 与原来数据点  两点之间的距离。因而导致了生成效果的不同，以及训练难度的不同。

参考文献：

• VAE 原理
• hwalsuklee/tensorflow-generative-model-collections
• summer：《Conditional Image Synthesis with Auxiliary Classifier GANs》阅读笔记

• ---

变分自编码器VAE：原来是这么一回事 | 附开源代码

作者丨苏剑林

单位丨广州火焰信息科技有限公司

研究方向丨NLP，神经网络

个人主页丨kexue.fm

过去虽然没有细看，但印象里一直觉得变分自编码器（Variational Auto-Encoder，VAE）是个好东西。趁着最近看概率图模型的三分钟热度，我决定也争取把 VAE 搞懂。

于是乎照样翻了网上很多资料，无一例外发现都很含糊，主要的感觉是公式写了一大通，还是迷迷糊糊的，最后好不容易觉得看懂了，再去看看实现的代码，又感觉实现代码跟理论完全不是一回事啊。

终于，东拼西凑再加上我这段时间对概率模型的一些积累，并反复对比原论文 Auto-Encoding Variational Bayes，最后我觉得我应该是想明白了。

其实真正的 VAE，跟很多教程说的的还真不大一样，很多教程写了一大通，都没有把模型的要点写出来。于是写了这篇东西，希望通过下面的文字，能把 VAE 初步讲清楚。

分布变换

通常我们会拿 VAE 跟 GAN 比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量 Z 生成目标数据 X 的模型，但是实现上有所不同。

更准确地讲，它们是假设了服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型 X=g(Z)，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

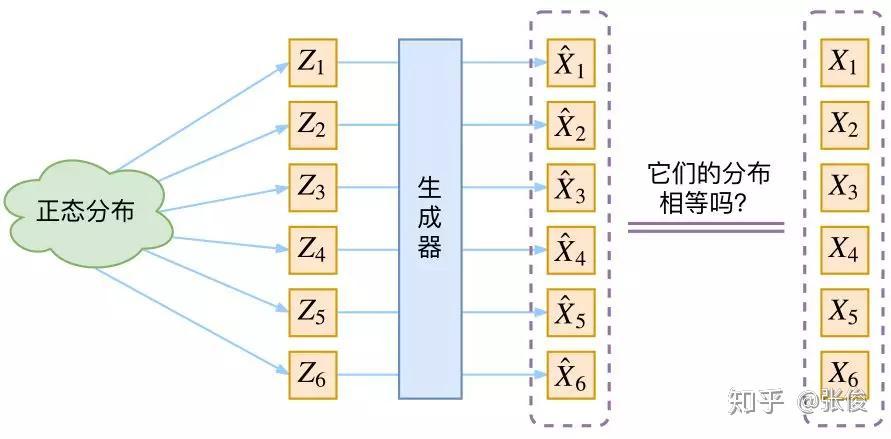
生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式。

那现在假设服从标准的正态分布，那么我就可以从中采样得到若干个 Z1,Z2,…,Zn，然后对它做变换得到 X̂1=g(Z1),X̂2=g(Z2),…,X̂n=g(Zn)，我们怎么判断这个通过 f 构造出来的数据集，它的分布跟我们目标的数据集分布是不是一样的呢？

有读者说不是有 KL 散度吗？当然不行，因为 KL 散度是根据两个概率分布的表达式来算它们的相似度的，然而目前我们并不知道它们的概率分布的表达式。

我们只有一批从构造的分布采样而来的数据 {X̂1,X̂2,…,X̂n}，还有一批从真实的分布采样而来的数据 {X1,X2,…,Xn}（也就是我们希望生成的训练集）。我们只有样本本身，没有分布表达式，当然也就没有方法算 KL 散度。

虽然遇到困难，但还是要想办法解决的。GAN 的思路很直接粗犷：既然没有合适的度量，那我干脆把这个度量也用神经网络训练出来吧。

就这样，WGAN 就诞生了，详细过程请参考互怼的艺术：从零直达 WGAN-GP。而 VAE 则使用了一个精致迂回的技巧。

VAE慢谈

这一部分我们先回顾一般教程是怎么介绍 VAE 的，然后再探究有什么问题，接着就自然地发现了 VAE 真正的面目。

经典回顾

首先我们有一批数据样本 {X1,…,Xn}，其整体用 X 来描述，我们本想根据 {X1,…,Xn} 得到 X 的分布 p(X)，如果能得到的话，那我直接根据 p(X) 来采样，就可以得到所有可能的 X 了（包括 {X1,…,Xn} 以外的），这是一个终极理想的生成模型了。

当然，这个理想很难实现，于是我们将分布改一改：

这里我们就不区分求和还是求积分了，意思对了就行。此时 p(X|Z) 就描述了一个由 Z 来生成 X的模型，而我们假设 Z 服从标准正态分布，也就是 p(Z)=N(0,I)。如果这个理想能实现，那么我们就可以先从标准正态分布中采样一个 Z，然后根据 Z 来算一个 X，也是一个很棒的生成模型。

接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现。框架的示意图如下：

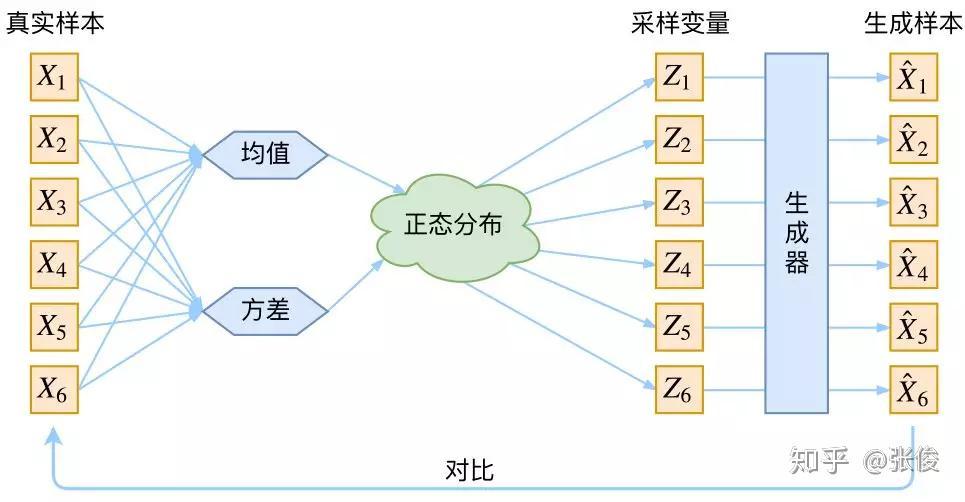
▲ VAE的传统理解

看出了什么问题了吗？如果像这个图的话，我们其实完全不清楚：究竟经过重新采样出来的Zk，是不是还对应着原来的 Xk，所以我们如果直接最小化 D(X̂ k,Xk)^2（这里 D 代表某种距离函数）是很不科学的，而事实上你看代码也会发现根本不是这样实现的。

也就是说，很多教程说了一大通头头是道的话，然后写代码时却不是按照所写的文字来写，可是他们也不觉得这样会有矛盾。

VAE初现

其实，在整个 VAE 模型中，我们并没有去使用 p(Z)（先验分布）是正态分布的假设，我们用的是假设 p(Z|X)（后验分布）是正态分布。

具体来说，给定一个真实样本 Xk，我们假设存在一个专属于 Xk 的分布 p(Z|Xk)（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。

为什么要强调“专属”呢？因为我们后面要训练一个生成器 X=g(Z)，希望能够把从分布 p(Z|Xk) 采样出来的一个 Zk 还原为 Xk。

如果假设 p(Z) 是正态分布，然后从 p(Z) 中采样一个 Z，那么我们怎么知道这个 Z对应于哪个真实的 X 呢？现在 p(Z|Xk) 专属于 Xk，我们有理由说从这个分布采样出来的 Z 应该要还原到Xk 中去。

事实上，在论文 Auto-Encoding Variational Bayes 的应用部分，也特别强调了这一点：

In this case, we can let the variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:

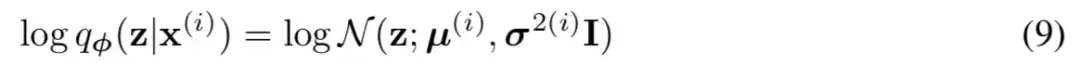
论文中的式 (9) 是实现整个模型的关键，不知道为什么很多教程在介绍 VAE 时都没有把它凸显出来。尽管论文也提到 p(Z) 是标准正态分布，然而那其实并不是本质重要的。

再次强调，这时候每一个 Xk 都配上了一个专属的正态分布，才方便后面的生成器做还原。但这样有多少个 X 就有多少个正态分布了。我们知道正态分布有两组参数：均值 μ 和方差 σ^2（多元的话，它们都是向量）。

那我怎么找出专属于 Xk 的正态分布 p(Z|Xk) 的均值和方差呢？好像并没有什么直接的思路。

那好吧，我就用神经网络来拟合出来。这就是神经网络时代的哲学：难算的我们都用神经网络来拟合，在 WGAN 那里我们已经体验过一次了，现在再次体验到了。

于是我们构建两个神经网络 μk=f1(Xk)，logσ^2=f2(Xk) 来算它们了。我们选择拟合 logσ^2 而不是直接拟合 σ^2，是因为 σ^2 总是非负的，需要加激活函数处理，而拟合 logσ^2 不需要加激活函数，因为它可正可负。

到这里，我能知道专属于 Xk 的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个 Zk 出来，然后经过一个生成器得到 X̂k=g(Zk)。

现在我们可以放心地最小化 D(X̂k,Xk)^2，因为 Zk 是从专属 Xk 的分布中采样出来的，这个生成器应该要把开始的 Xk 还原回来。于是可以画出 VAE 的示意图：

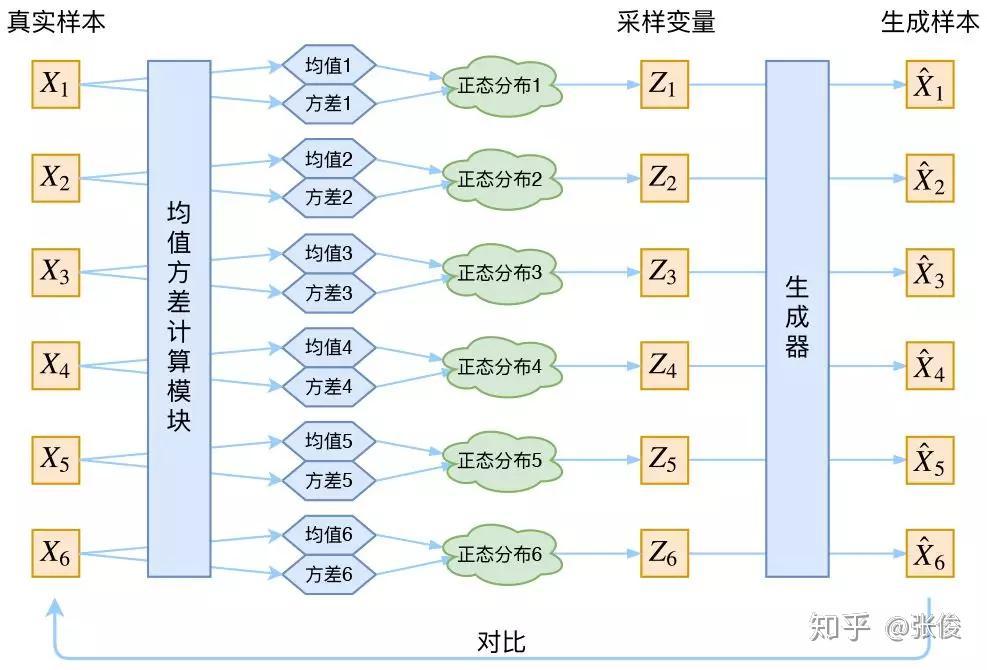
事实上，VAE 是为每个样本构造专属的正态分布，然后采样来重构。

分布标准化

让我们来思考一下，根据上图的训练过程，最终会得到什么结果。

首先，我们希望重构 X，也就是最小化 D(X̂k,Xk)^2，但是这个重构过程受到噪声的影响，因为Zk 是通过重新采样过的，不是直接由 encoder 算出来的。

显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差）通过一个神经网络算出来的，所以最终模型为了重构得更好，肯定会想尽办法让方差为0。

而方差为 0 的话，也就没有随机性了，所以不管怎么采样其实都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。

说白了，模型会慢慢退化成普通的 AutoEncoder，噪声不再起作用。

这样不就白费力气了吗？说好的生成模型呢？

别急别急，其实 VAE 还让所有的 p(Z|X) 都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。

怎么理解“保证了生成能力”呢？如果所有的 p(Z|X) 都很接近标准正态分布 N(0,I)，那么根据定义：

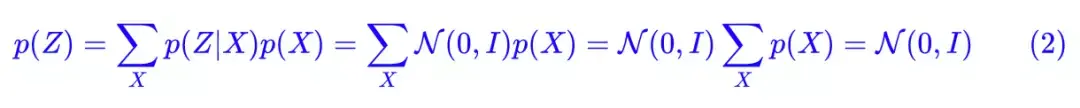
这样我们就能达到我们的先验假设：p(Z) 是标准正态分布。然后我们就可以放心地从 N(0,I) 中采样来生成图像了。

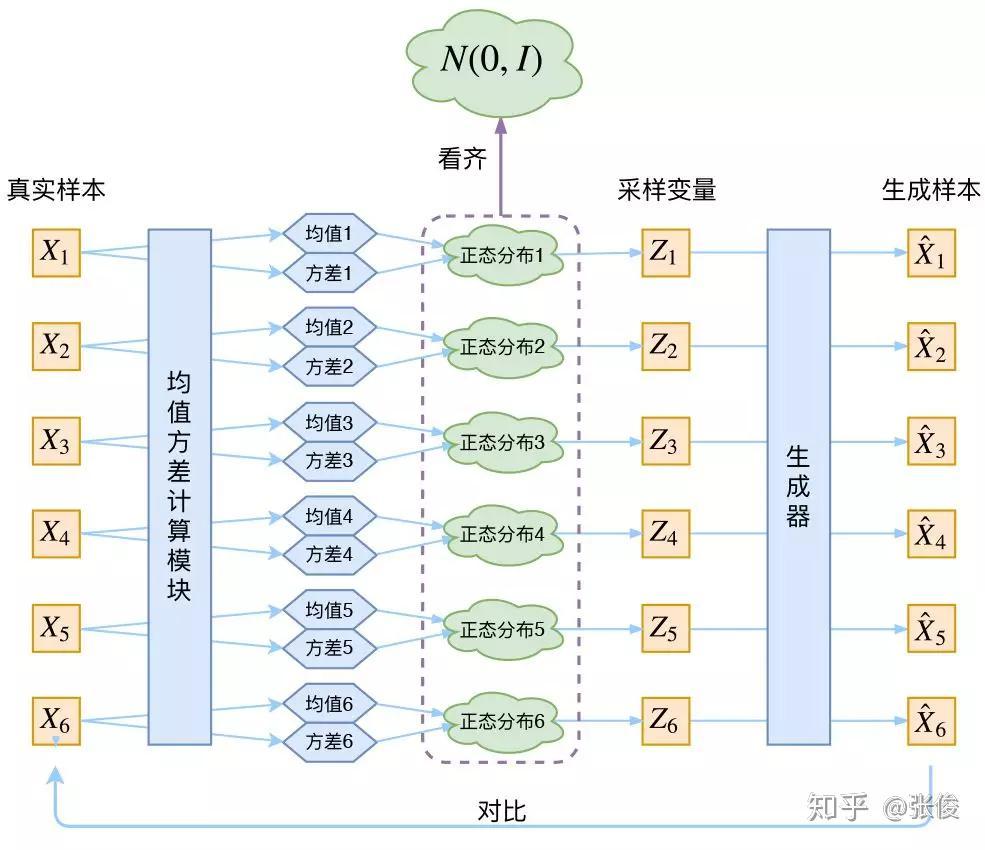
为了使模型具有生成能力，VAE 要求每个 p(Z_X) 都向正态分布看齐。

那怎么让所有的 p(Z|X) 都向 N(0,I) 看齐呢？如果没有外部知识的话，其实最直接的方法应该是在重构误差的基础上中加入额外的 loss：

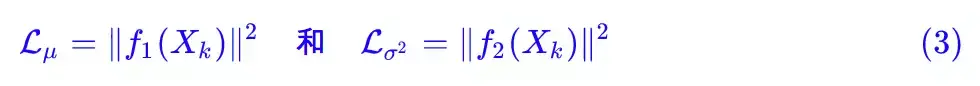
因为它们分别代表了均值 μk 和方差的对数 logσ^2，达到 N(0,I) 就是希望二者尽量接近于 0 了。不过，这又会面临着这两个损失的比例要怎么选取的问题，选取得不好，生成的图像会比较模糊。

所以，原论文直接算了一般（各分量独立的）正态分布与标准正态分布的 KL 散度KL(N(μ,σ^2)‖N(0,I))作为这个额外的 loss，计算结果为：

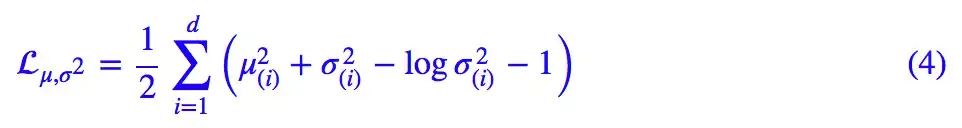
这里的 d 是隐变量 Z 的维度，而 μ(i) 和 σ_{(i)}^{2} 分别代表一般正态分布的均值向量和方差向量的第 i 个分量。直接用这个式子做补充 loss，就不用考虑均值损失和方差损失的相对比例问题了。

显然，这个 loss 也可以分两部分理解：

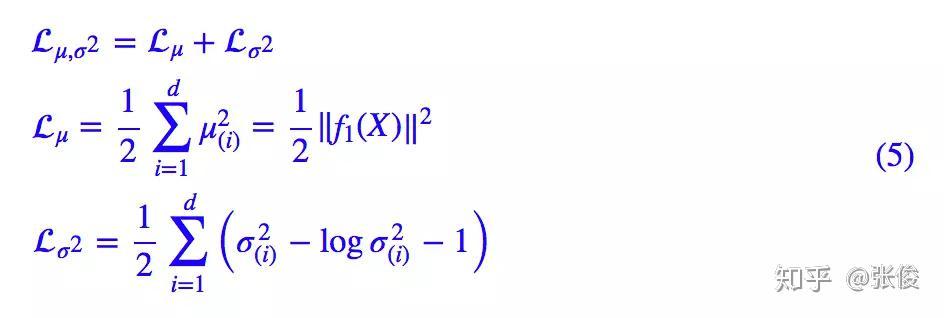
推导

由于我们考虑的是各分量独立的多元正态分布，因此只需要推导一元正态分布的情形即可，根据定义我们可以写出：

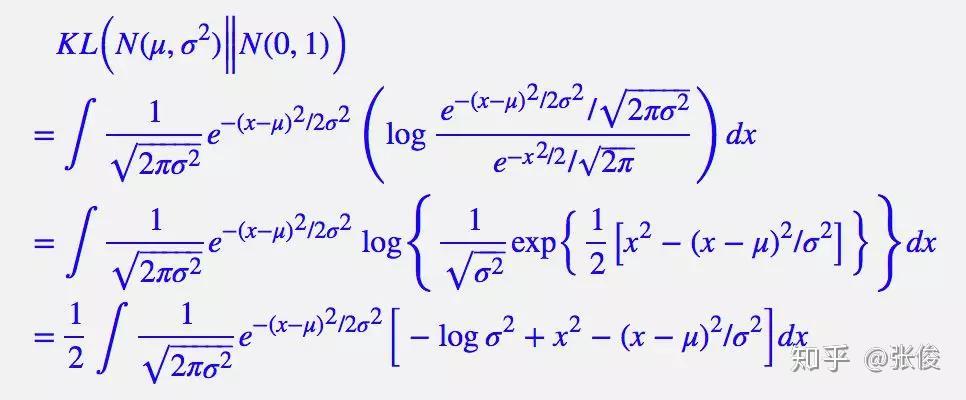
整个结果分为三项积分，第一项实际上就是 −logσ^2 乘以概率密度的积分（也就是 1），所以结果是 −logσ^2；第二项实际是正态分布的二阶矩，熟悉正态分布的朋友应该都清楚正态分布的二阶矩为 μ^2+σ^2；而根据定义，第三项实际上就是“-方差除以方差=-1”。所以总结果就是：

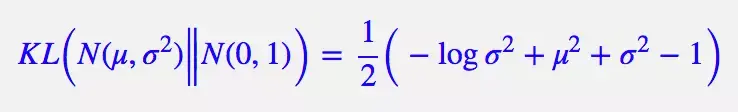
重参数技巧

最后是实现模型的一个技巧，英文名是 Reparameterization Trick，我这里叫它做重参数吧。

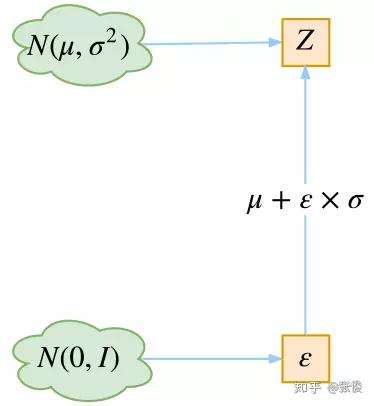
▲ 重参数技巧

其实很简单，就是我们要从 p(Z|Xk) 中采样一个 Zk 出来，尽管我们知道了 p(Z|Xk) 是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的，于是我们利用了一个事实：

所以，我们将从 N(μ,σ^2) 采样变成了从 N(μ,σ^2) 中采样，然后通过参数变换得到从N(μ,σ^2) 中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。

具体怎么实现，大家把上述文字对照着代码看一下，一下子就明白了。

后续分析

即便把上面的所有内容都搞清楚了，面对 VAE，我们可能还存有很多疑问。

本质是什么

VAE 的本质是什么？VAE 虽然也称是 AE（AutoEncoder）的一种，但它的做法（或者说它对网络的诠释）是别具一格的。

在 VAE 中，它的 Encoder 有两个，一个用来计算均值，一个用来计算方差，这已经让人意外了：Encoder 不是用来 Encode 的，是用来算均值和方差的，这真是大新闻了，还有均值和方差不都是统计量吗，怎么是用神经网络来算的？

事实上，我觉得 VAE 从让普通人望而生畏的变分和贝叶斯理论出发，最后落地到一个具体的模型中，虽然走了比较长的一段路，但最终的模型其实是很接地气的。

它本质上就是在我们常规的自编码器的基础上，对 encoder 的结果（在VAE中对应着计算均值的网络）加上了“高斯噪声”，使得结果 decoder 能够对噪声有鲁棒性；而那个额外的 KL loss（目的是让均值为 0，方差为 1），事实上就是相当于对 encoder 的一个正则项，希望 encoder 出来的东西均有零均值。 

那另外一个 encoder（对应着计算方差的网络）的作用呢？它是用来动态调节噪声的强度的。

直觉上来想，当 decoder 还没有训练好时（重构误差远大于 KL loss），就会适当降低噪声（KL loss 增加），使得拟合起来容易一些（重构误差开始下降）。

反之，如果 decoder 训练得还不错时（重构误差小于 KL loss），这时候噪声就会增加（KL loss 减少），使得拟合更加困难了（重构误差又开始增加），这时候 decoder 就要想办法提高它的生成能力了。

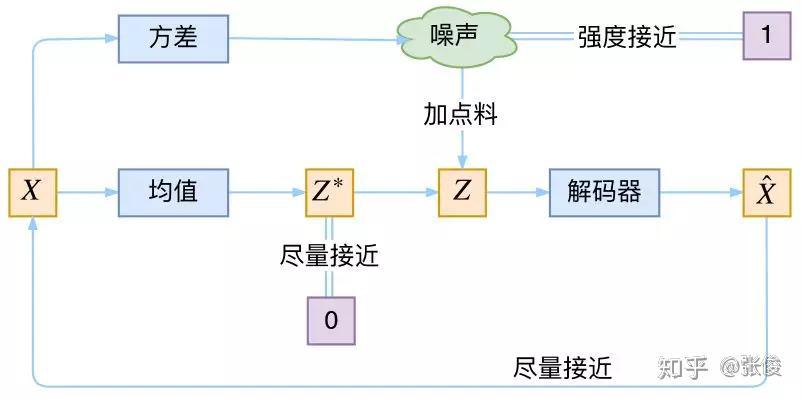
▲ VAE的本质结构

说白了，重构的过程是希望没噪声的，而 KL loss 则希望有高斯噪声的，两者是对立的。所以，VAE 跟 GAN 一样，内部其实是包含了一个对抗的过程，只不过它们两者是混合起来，共同进化的。

从这个角度看，VAE 的思想似乎还高明一些，因为在 GAN 中，造假者在进化时，鉴别者是安然不动的，反之亦然。当然，这只是一个侧面，不能说明 VAE 就比 GAN 好。

GAN 真正高明的地方是：它连度量都直接训练出来了，而且这个度量往往比我们人工想的要好（然而 GAN 本身也有各种问题，这就不展开了）。

正态分布？

对于 p(Z|X) 的分布，读者可能会有疑惑：是不是必须选择正态分布？可以选择均匀分布吗？

首先，这个本身是一个实验问题，两种分布都试一下就知道了。但是从直觉上来讲，正态分布要比均匀分布更加合理，因为正态分布有两组独立的参数：均值和方差，而均匀分布只有一组。

前面我们说，在 VAE 中，重构跟噪声是相互对抗的，重构误差跟噪声强度是两个相互对抗的指标，而在改变噪声强度时原则上需要有保持均值不变的能力，不然我们很难确定重构误差增大了，究竟是均值变化了（encoder的锅）还是方差变大了（噪声的锅）。

而均匀分布不能做到保持均值不变的情况下改变方差，所以正态分布应该更加合理。

变分在哪里

还有一个有意思（但不大重要）的问题是：VAE 叫做“变分自编码器”，它跟变分法有什么联系？在VAE 的论文和相关解读中，好像也没看到变分法的存在？

其实如果读者已经承认了 KL 散度的话，那 VAE 好像真的跟变分没多大关系了，因为 KL 散度的定义是：

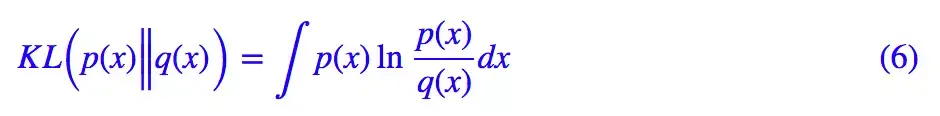
如果是离散概率分布就要写成求和，我们要证明：已概率分布 p(x)（或固定q(x)）的情况下，对于任意的概率分布 q(x)（或 p(x)），都有KLp(x)‖q(x))≥0，而且只有当p(x)=q(x)时才等于零。

因为 KL(p(x)‖q(x))实际上是一个泛函，要对泛函求极值就要用到变分法，当然，这里的变分法只是普通微积分的平行推广，还没涉及到真正复杂的变分法。而 VAE 的变分下界，是直接基于 KL 散度就得到的。所以直接承认了 KL 散度的话，就没有变分的什么事了。

一句话，VAE 的名字中“变分”，是因为它的推导过程用到了 KL 散度及其性质。

条件VAE

最后，因为目前的 VAE 是无监督训练的，因此很自然想到：如果有标签数据，那么能不能把标签信息加进去辅助生成样本呢？

这个问题的意图，往往是希望能够实现控制某个变量来实现生成某一类图像。当然，这是肯定可以的，我们把这种情况叫做 Conditional VAE，或者叫 CVAE（相应地，在 GAN 中我们也有个 CGAN）。

但是，CVAE 不是一个特定的模型，而是一类模型，总之就是把标签信息融入到 VAE 中的方式有很多，目的也不一样。这里基于前面的讨论，给出一种非常简单的 VAE。

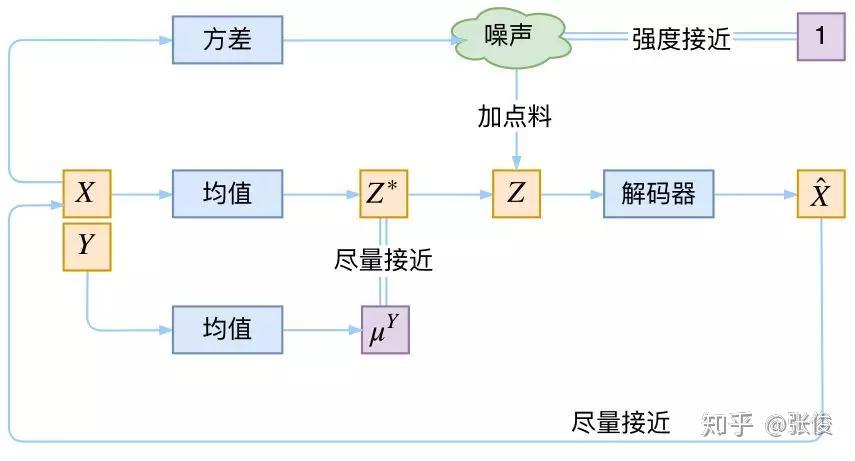
▲ 一个简单的CVAE结构

在前面的讨论中，我们希望 X 经过编码后，Z 的分布都具有零均值和单位方差，这个“希望”是通过加入了 KL loss 来实现的。

如果现在多了类别信息 Y，我们可以希望同一个类的样本都有一个专属的均值μ^Y（方差不变，还是单位方差），这个 μ^Y 让模型自己训练出来。

这样的话，有多少个类就有多少个正态分布，而在生成的时候，我们就可以通过控制均值来控制生成图像的类别。

事实上，这样可能也是在 VAE 的基础上加入最少的代码来实现 CVAE 的方案了，因为这个“新希望”也只需通过修改 KL loss 实现：

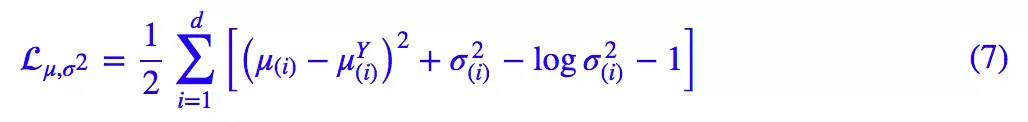
下图显示这个简单的 CVAE 是有一定的效果的，不过因为 encoder 和 decoder 都比较简单（纯 MLP），所以控制生成的效果不尽完美。

用这个 CVAE 控制生成数字 9，可以发现生成了多种样式的 9，并且慢慢向 7 过渡，所以初步观察这种 CVAE 是有效的。

更完备的 CVAE 请读者自行学习了，最近还出来了 CVAE 与 GAN 结合的工作 CVAE-GAN: Fine-Grained Image Generation through Asymmetric Training，模型套路千变万化。

代码

我把 Keras 官方的 VAE 代码复制了一份，然后微调并根据前文内容添加了中文注释，也把最后说到的简单的 CVAE 实现了一下，供读者参考。

代码：https://github.com/bojone/vae

终点站

磕磕碰碰，又到了文章的终点了。不知道讲清楚了没，希望大家多提点意见。

总的来说，VAE 的思路还是很漂亮的。倒不是说它提供了一个多么好的生成模型（因为事实上它生成的图像并不算好，偏模糊），而是它提供了一个将概率图跟深度学习结合起来的一个非常棒的案例，这个案例有诸多值得思考回味的地方。

点击以下标题查看相关内容：

• PaperWeekly 第二十七期 | VAE for NLP
• End-to-End任务驱动对话与数据库的衔接

本文由 AI 学术社区 PaperWeekly 精选推荐，社区目前已覆盖自然语言处理、计算机视觉、人工智能、机器学习、数据挖掘和信息检索等研究方向，点击即刻加入社区！

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。

微信公众号：PaperWeekly

新浪微博：@PaperWeekly

• 

  Jian wang1 年前

  有读者说不是有 KL 散度吗？当然不行，因为 KL 散度是根据两个概率分布的表达式来算它们的相似度的，然而目前我们并不知道它们的概率分布的表达式。

  这个表达可能不准确，其实根据两个分布的直方图可以直接计算kl距离，并不要求知道分布的具体形式

  ​16​回复​踩​举报

• 

  Saturn1 年前

  我的一点疑问是，到底是一个特定样本X_k对应一个隐变量z_k呢，还是一个特定样本X_k对应隐变量z_k的分布呢？如果我们想要在N(0,1)上采样z并且生成X，那么我们的z和X应该是一一对应的，而不是z的分布和X是一一对应的。但我们的模型却要最小化重构误差，让X_k对应的z_k分布尽可能包含X_k样本的信息，最后又要再最小化z的分布和N(0,1)，在N(0,1)上采样z来生成。。还是没有懂啊。

  ​赞​回复​踩​举报
• 

  荀迎曙回复Saturn11 个月前

  这个做法的目的是引入噪音，提高模型的泛化能力。比如极端点，假如一个网络死记硬背住了各个X和z的对应，也可以做到重构误差很低，但是没有任何泛化能力。强迫z必须从分布中取样，就是让网络不能这么干

  ​3​回复​踩​举报
• 

  利伯蒂回复荀迎曙11 个月前

  你好，我也有类似的疑问。按我的理解，模型要求所有样本图片经过编码后都服从标准正态分布，在生成一张新的图片时，则从标准正态分布中采样，然后传入解码器。那么既然都是从正态分布中采样，那么最后解码出的图片难道不都是一样的吗？同样的，对于图片重构，既然要求所有样本的隐变量都服从标准正态分布，那么编码得到的信息又是怎么被用上的？望解答，谢谢！

  ​1​回复​踩​举报

查看全部 6 条回复

• 

  如子1 年前

  为苏神疯狂打call

  ​1​回复​踩​举报

• 

  张枫1 年前

  请问GAN生成器怎么样学习样本分布的呢？

  ​赞​回复​踩​举报

• 

  陈辉1 年前

  请问如何理解VAE的对抗性？我觉得，重构loss和规范化loss训练时是一起训练的，不会让其他一个最优，再去优化另外一个。那么，这个和GAN的对抗性很不一样。用trade-off是不是更合适一点？

  ​1​回复​踩​举报

• 

  psubunwell1 年前

  感谢！

  ​赞​回复​踩​举报

• 

  笨笨1 年前

  您好，我想问一下p(Z|X)的均值和方差是怎么计算的，因为在您给的代码里是‘z_mean = Dense(latent_dim)(h)；z_log_var = Dense(latent_dim)(h)’，我觉得这两个量是同一个值啊，并且一直很疑惑为什么前面的Encoder可以同时产生均值和方差。

  ​赞​回复​踩​举报
• 

  隔壁小王回复笨笨1 年前

  他这个encoder就是个神经网络的全连接层。输入通过全连接得到特定维度的输出，如果输出是2维度（对于单个样本）。则这两个维度就是方差和期望呀

  ​赞​回复​踩​举报
• 

  贝鲁姆回复笨笨11 个月前

  这两行是在构建学习mean 和 var 的神经层，并不是具体的返回值。 另外，mean 和

  var 应该分别是一个vector。

  ​赞​回复​踩​举报

展开其他 2 条回复

• 

  zc lin1 年前

  其实真的这么复杂吗……我感觉VAE只是一个解带潜变量的有向概率图的方法而已啊 只是定义概率分布的时候用神经网络参数化 再加个重参数化trick求解 原则上也不一定要用高斯分布吧

  ​3​回复​踩​举报

• 

  SMON1 年前

  想问个问题，由于VAE的对抗性，是不是用已经训练好的模型的encoder输出Z，对decoder单独重新训练就不行了？

  ​赞​回复​踩​举报
• 

  荀迎曙回复SMON11 个月前

  感觉不行吧，用其他方式训练好的encoder输出的Z不符合高斯分布，如果要重新训练Z符合高斯，势必要调整encoder

  ​赞​回复​踩​举报

• 

  隔壁小王1 年前

  请教下：直觉上来想，当 decoder 还没有训练好时（重构误差远大于 KL loss），就会适当降低噪声（KL loss 增加），使得拟合起来容易一些（重构误差开始下降）。

  这句话该怎么理解

  ​1​回复​踩​举报

• 

  荀迎曙11 个月前

  写得真好，彻底搞懂了

  ​1​回复​踩​举报

• 

  十茗9 个月前

  我说说自己的理解，其实VAE的可以看成一个做降维的model，我们希望把一个高维的特征投影到一个低维的流型上，而在VAE中，这个低维流型就是一个多元标准正态分布。为了使投影准确，于是通过希望每一个样本Xi的计算出来的期望与方差都接近与我们希望投影的分布，所以这里就有了相对熵损失。至于重构损失，我大胆地猜测，是可以使采样的时候更加准确，能够采样到我们在encode的时候投影到的点。（如果不这样想，我实在不理解为什么随机采样能保证encode和decode过程的一致性）。。。

  ​2​回复​踩​举报

• 

  莫显博8 个月前

  受教了，网上看了很多教程，思想跟实现都有点矛盾，看了作者这个非常清晰，感谢！

  ​1​回复​踩​举报

• 

  wingwind7 个月前

  我觉得你说的xk专属zk的问题，是因为对图中的xk理解不同吧？很多VAE描述的图（和文中的传统描述图不同，不把z拆开画的），每一个xi应该是指一个step，而不是一个完整的样本，所以这并不说是所有样本属于同一个z分布。而下面你画的图每一个xk是一个完整的样本了，所以要分开画，每一个xk对应一个zk。也就是说，论文xi的那个i是上标，其他介绍VAE的"传统描述图"xk的k应该是下标。。

  ​7​回复​踩​举报

• 

  卡马壬5 个月前

  你说的（9）其实是个基本问题 根本不需要强调。本来的latent variable model 就是（X_i|Zi）(X_i | U,\sigma).

  ​赞​回复​踩​举报

• 

  秦睿5 个月前

  有一点我真没看明白，请指点下。kl越小，噪音越大，能解释下吗？

  ​赞​回复​踩​举报

• 

  黄鑫NAT4 个月前

  有两个问题希望大神能给与解答。

  1.对encoder的结果施加方差为1的干扰是希望模型具备生成的鲁棒性，那为什么要为均值施加mean=0的约束呢？这个的目的是什么？

  2.如果是普通的VAE出来的结果，每个样本是对应一个不同的\mu和\sigma，那同一各个类的不同样本，他们的\mu和\sigma有没有什么关系呢？是不是必须要像condition-VAE那样施加类别上的约束才能让同类别的样本的hidden vector存在相似性？

  ​赞​回复​踩​举报

---