线性回归Linear regression

线性回归算法

解决回归问题
思想简单，容易实现
是许多强大的非线性模型的基础
结果具有很好的可解释性
蕴含机器学习中的很多重要思想

基本思想：寻找一条直线，最大程度的“拟合”样本特征和样本输出标记之间的关系

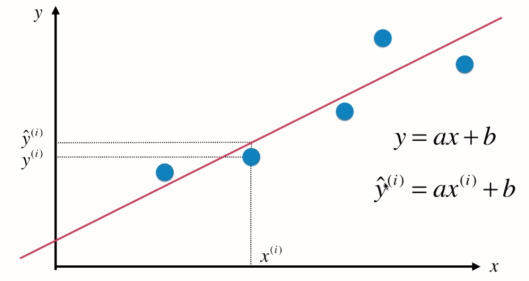
如横轴房屋面积，纵轴房屋价格

由实际值x⁽ⁱ⁾代入到拟合直线方程中得到的y_hat，即y的预测值。

假设找到最佳拟合的直线方程：y = ax + b, 则对于每一个样本点x⁽ⁱ⁾，根据直线方程其预测值为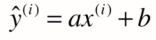：， 真值为y⁽ⁱ⁾。

因此，我们当然希望y⁽ⁱ⁾和y_hat⁽ⁱ⁾的差距尽量小。其差距可表示为：

（用绝对值表示的话，它不是一个处处可导的表达式，不便于后续计算）

考虑所有样本，其总差距为：

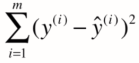
理所当然，我们希望其总差距尽可能小，将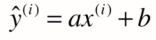代入上式可得：

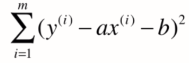------------------------（1）

（在(1)式中，只有a，b两个未知数，监督学习中x⁽ⁱ⁾和y⁽ⁱ⁾都是已知数。）

损失函数：度量出模型没有拟合住的那一部分

效用函数：度量拟合的程度

一类机器学习算法的基本思路：

通过分析问题，确定问题的损失函数或效用函数；通过最优化损失函数或效用函数，获得机器学习的模型。近乎所有参数学习的算法都是这样的套路。

如线性回归，多项式回归，逻辑回归，SVM，神经网络，...

它们都是学习相应参数来最优化其目标函数。其区别在于他们的模型不同，建立的目标函数不同，优化的方式不同。

P.S.

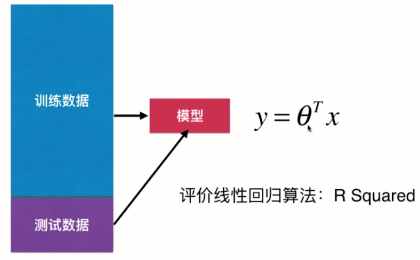
对于分类问题（左图），横纵坐标都是样本的特征，输出标记由点是红色还是蓝色表示。而对于回归问题（右图），纵轴是样本的输出标记。

因为在回归问题中，我们需要预测的是连续的值，而不是简单的用红色蓝色就可以表示。因此当要表示两个特征的回归问题时，就需要在三维空间中进行数据可视化。

样本特征只有一个，称为：简单线性回归

样本特征多个，多元线性回归

多元线性回归

数据有多少个特征，相应前面就有多少个系数(西塔1到西塔n，西塔0是截距)，对比简单线性回归，a是西塔1，b就是西塔0，区别就是特征数从1拓展到了n

其中，

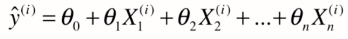
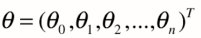（写出列向量的形式，所以加了一个转置）--------（1）

为了使式子看起来更一致，方便后续推导，我们加上第0个特征，其值恒等于1，

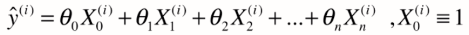
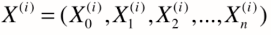（行向量的形式。对于X来说，每一行代表一个样本，每一列代表一个特征。X⁽ⁱ⁾代表从X中抽出一行）----------（2）

结合（1）（2），可将 y 的预测值写成，

（相乘再相加->点乘）

推广到所有样本，

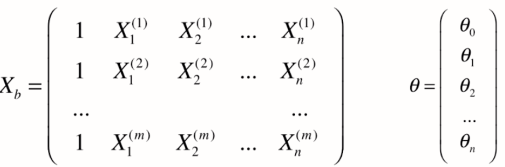
Xb (m*(n+1)) 与 X (m*n) 区分开，区别在于多了第一列我们虚拟出来的列，值全部为1。西塔为有n+1个元素的列向量。其中西塔0 是截距，剩下的西塔1 到西塔n 是系数coefficients. 西塔0 与数据特征无关，其只表示偏移，剩下的西塔与数据特征相关。

综上，

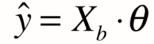（y_hat 得到的值是一个列向量，其有m个元素，每个元素对应原来的大X中每一个样本经过西塔后得到的预测值）

目标，

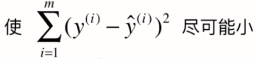
平方的和的形式可表示成两个向量点乘的形式，因此目标可写成，

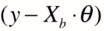本来是列向量(m * 1)，转置完成了行向量(1*m)。相乘的结果是一个值。

总结，

看起来这个式子很好，给Xb和y就能求出西塔，但为问题是其实现时间复杂度高: O(n^3)，即使优化了，复杂度也有n^2.4。

其优点是不需要对数据做归一化处理，它没有量纲的问题。直接将数据通过数学公式的运算就可以得到系数的值。这点与KNN不同。

=====>解决方案

线性回归算法总结

典型参数学习
- 对比KNN：非参数学习
只能解决回归问题
- 　　虽然很多分类方法中线性回归是基础（如逻辑回归）
- 对比KNN：既可解决分类问题，也可解决回归问题
对数据有假设：线性
- 　　对比KNN对数据没有假设
优点：对数据具有强解释性。（白盒）