【状压+状态转移】A Famous Airport Managere

https://www.bnuoj.com/v3/problem_show.php?pid=25653

【题意】

• 给定一个3*3的九宫格，模拟一个停机坪。第一个格子一定是'*',代表take off area,其他的格子可能是'*','B','G'中的一种,'*'代表空地,'B','G'代表蓝色和绿色的飞机。
• 每次操作都是一个飞机移动到take off area并起飞，在这个过程中其他飞机不能动。
• 问有多少种飞机起飞的不同序列，同一种颜色的飞机是一模一样的。

【思路】

• 这个停机坪最多有3^8=6561中不同的状态，可以考虑用三进制状压。
• 状态之间可以转移。比如：

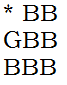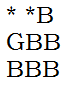可以由转移来，也就是当前的出队序列就是B+pre的出队序列。

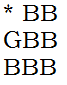可以由转移来，也就是当前的出队序列就是G+pre的出队序列。

• 这个出队序列也可以状压，为了表示方便，我们把当前的出队序列表示为pre的出队序列后面接上B或G,这样就可以用[pre]*3+1或[pre]*3+2表示当前状态。
• 使用set可以自动去重，去掉重复的状态。

【Accepted】

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<cmath>
 #include<algorithm>
 #include<set>
 #include<queue>
 using namespace std;
 const int maxn=;
 const int inf=0x3f3f3f3f;
 char s[][];
 int a[];
 int dig[];
 set<int> dp[maxn];
 set<int>:: iterator it;
 bool v[][];
 int dir[][]={{,},{,},{,-},{-,}};
 void init()
 {
     dig[]=;
     for(int i=;i<=;i++)
     {
         dig[i]=dig[i-]*;
     }
 }

 void BFS()
 {
     queue<pair<int,int> >Q;
     memset(v,false,sizeof(v));
     Q.push(make_pair(,));
     v[][]=true;
     while(!Q.empty())
     {
         int x=Q.front().first;
         int y=Q.front().second;
         Q.pop();
     //    cout<<x<<" "<<y<<endl;
         for(int i=;i<;i++)
         {
             int xx=x+dir[i][];
             int yy=y+dir[i][];
             if(v[xx][yy])
             {
                 continue;
             }
             if(xx<||x>=||y<||y>=)
             {
                 continue;
             }
             v[xx][yy]=true;
             if(s[xx][yy]=='*')
             {
                 Q.push(make_pair(xx,yy));
             }
         }
     }
 }

 void DP()
 {
     dp[].insert();
     for(int i=;i<dig[];i++)
     {
         int now=i;
         for(int j=;j<;j++)
         {
             a[-j]=now%;
             now/=;
         }
         for(int j=;j<;j++)
         {
             for(int k=;k<;k++)
             {
                 if(a[j*+k]==)
                 {
                     s[j][k]='*';
                 }
                 else if(a[j*+k]==)
                 {
                     s[j][k]='B';
                 }
                 else
                 {
                     s[j][k]='G';
                 }
             }
         }
         BFS();
         for(int j=;j<;j++)
         {
             for(int k=;k<;k++)
             {
                 if(v[j][k]&&s[j][k]=='B')
                 {
                     int pre=i-*dig[-*j-k];
                     for(it=dp[pre].begin();it!=dp[pre].end();it++)
                     {
                         dp[i].insert(*(it)*+);
                     }
                 }
                 else if(v[j][k]&&s[j][k]=='G')
                 {
                     int pre=i-*dig[-*j-k];
                     for(it=dp[pre].begin();it!=dp[pre].end();it++)
                     {
                         dp[i].insert(*(it)*+);
                     }
                 }
             }
         }
     }
 }
 int main()
 {
     init();
     DP();
     int cas=;
     while(~scanf("%s%s%s",s[],s[],s[]))
     {
         for(int i=;i<;i++)
         {
             for(int k=;k<;k++)
             {
                 if(s[i][k]=='*')
                 {
                     a[*i+k]=;
                 }
                 else if(s[i][k]=='B')
                 {
                     a[*i+k]=;
                 }
                 else
                 {
                     a[*i+k]=;
                 }
             }
         }
         int now=;
         for(int i=;i<;i++)
         {
             now+=a[i]*dig[-i];
         }
         printf("Case %d: ",++cas);
         cout<<dp[now].size()<<endl;
     }

     return ;
 }