[Codeforces Round #461 (Div2)] 题解

[比赛链接]

http://codeforces.com/contest/922

[题解]

Problem A. Cloning Toys

         [算法]

当y = 0 ,   不可以

当y = 1 , x不为0时 ， 不可以

当 y - 1 <= x , (x - y + 1)为偶数时 ， 可以

时间复杂度 : O(1)

[代码]

#include<bits/stdc++.h>
using namespace std;
 
template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); }
template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); }
template <typename T> inline void read(T &x)
{
    T f = ; x = ;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = (x << ) + (x << ) + c - '';
    x *= f;
}
 
int main()
{
 
        int x , y;
        read(x); read(y);
        if (y == ) printf("No\n");
        else if (y ==  && x != ) printf("No\n");
        else if (y -  <= x && (x - y + ) %  == ) printf("Yes\n");
        else printf("No\n");
 
        return ;
 
}

Problem B. Magic Forest

              [算法]

枚举三角形的两边 ， 计算第三边 ， 判断是否能构成三角形即可

时间复杂度 : O(N^2)

[代码]

#include<bits/stdc++.h>
using namespace std;
 
int n;
 
template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); }
template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); }
template <typename T> inline void read(T &x)
{
    T f = ; x = ;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = (x << ) + (x << ) + c - '';
    x *= f;
}
inline bool ok(int x,int y,int z)
{
        return x >  && y >  && z >  && x <= n && y <= n && z <= n && x + y > z && x + z > y && y + z > x;
}
 
int main()
{
 
        int answer = ;
        read(n);
        for (int i = ; i <= n; i++)
        {
                for (int j = ; j <= n; j++)
                {
                        int k = i ^ j;
                        if (ok(i,j,k)) answer++;
                }
        }
        answer /= ;
        printf("%d\n",answer);
 
        return ;
 
}

Problem C. Cave Painting

                [算法]

一个数除以1余数只可能为0

一个数除以2余数只可能为0,1

....

一个数除以n余数只可能为0,1,2,...n - 1

因此 ， 我们只需判断对于i <= k , n除以i余数是否余数(i - 1)

时间复杂度 : O(K)

[代码]

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
 
template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); }
template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); }
template <typename T> inline void read(T &x)
{
    T f = ; x = ;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = (x << ) + (x << ) + c - '';
    x *= f;
}
 
int main()
{
 
        LL n , k;
        read(n); read(k);
        for (LL i = ; i <= k; i++)
        {
                if (n % i != i - )
                {
                        printf("No\n");
                        return ;
                }
        }
        printf("Yes\n");
 
        return ;
 
}

Problem D. Robot Vacuum Cleaner

                  [算法]

显然 ， 答案只与字符串中"s"和"h"的个数有关

若a.s * b.h > a.h * b.s ， a比b优

调用std :: sort即可 ， 时间复杂度 ： O(NlogN)

[代码]

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MAXN = 1e5 + ;
 
struct info
{
        int s , h;
} a[MAXN];
 
int n;
 
inline bool cmp(info a,info b)
{
        return 1ll * a.s * b.h > 1ll * b.s * a.h;
}
 
int main()
{
 
        cin >> n;
        LL ans = ;
        for (int i = ; i <= n; i++)
        {
                string s;
                cin >> s;
                for (int j = ; j < (int)s.size(); j++)
                {
                        if (s[j] == 'h')
                        {
                                a[i].h++;
                                ans += a[i].s;
                        } else a[i].s++;
                }
        }
        sort(a + ,a + n + ,cmp);
        int pre = ;
        for (int i = ; i <= n; i++)
        {
                ans += 1ll * pre * a[i].h;
                pre += a[i].s;
        }
        printf("%I64d\n",ans);
 
        return ;
 
}

Problem E. Birds

                      [算法]

注意 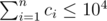.,考虑使用动态规划

用f[i][j]表示在前i只小鸟中选j只 ， 最多还剩多少能量 , 转移比较显然 ， 不再赘述

时间复杂度 : O(NV)

[代码]

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MAXN = 1e3 + ;
const LL MAXS = 1e4 + ;
const LL inf = 1e18;
 
LL n , W , B , X;
LL c[MAXN],cost[MAXN];
LL dp[MAXN][MAXS];
 
template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); }
template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); }
template <typename T> inline void read(T &x)
{
    T f = ; x = ;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = (x << ) + (x << ) + c - '';
    x *= f;
}
int main()
{
 
        read(n); read(W); read(B); read(X);
        for (LL i = ; i <= n; i++) read(c[i]);
        for (LL i = ; i <= n; i++) read(cost[i]);
        for (LL i = ; i <= n; i++)
        {
                for (LL j = ; j < MAXS; j++)
                {
                        dp[i][j] = -inf;
                }
        }
        LL cnt = c[];
        for (LL i = ; i <= c[]; i++)
        {
                if (W - 1LL * i * cost[] >= )
                        dp[][i] = min(W - 1LL * i * cost[] + X,W + i * B);
                else break;
        }
        for (LL i = ; i <= n; i++)
        {
                cnt += c[i];
                for (LL j = ; j <= cnt; j++)
                {
                        for (LL k = ; k <= min(j,c[i]); k++)
                        {
                                if (dp[i - ][j - k] == -inf) continue;
                                if (dp[i - ][j - k] - 1LL * cost[i] * k >= )
                                        chkmax(dp[i][j],min(1LL * W + 1LL * j * B,dp[i - ][j - k] + 1LL * X - 1LL * cost[i] * k));
                        }
                }
        }
        LL ans = ;
        for (LL i = ; i <= cnt; i++)
        {
                if (dp[n][i] >= )
                        ans = i;
        }
        printf("%I64d\n",ans);
 
        return ;
 
}

Problem F.  Divisbility

[算法]

用F(i)表示选取1-i ,  符合条件的二元组的个数

显然 ， 当k > F(n)时 ，  答案为No

否则 ， 若k < F(n / 2) ， 则不断将n降至n / 2

最后 ， 我们取出n  / 2 + 1至n ， 然后贪心删除一些数 ， 即可

时间复杂度 ： O(NlogN)

[代码]

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 3e5 + ;
typedef long long LL;
 
int n , k;
int d[MAXN];
vector< int > a[MAXN];
bool flg[MAXN];
 
template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); }
template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); }
template <typename T> inline void read(T &x)
{
    T f = ; x = ;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
    for (; isdigit(c); c = getchar()) x = (x << ) + (x << ) + c - '';
    x *= f;
}
inline LL f(int n)
{
        LL ret = ;
        for (int i = ; i <= n; i++) ret += 1LL * n / i - ;
        return ret;
}
 
int main()
{
 
        read(n); read(k);
        if (k > f(n))
        {
                printf("No\n");
                return ;
        }
        while (f(n >> ) >= k) n >>= ;
        for (int i = ; i <= n; i++)
        {
                for (int j =  * i; j <= n; j += i)
                {
                        ++d[j];
                }
        }
        for (int i = n /  + ; i <= n; i++) a[d[i]].push_back(i);
        memset(flg,true,sizeof(flg));
        int m = f(n) - k;
        for (int i = n; i >= ; i--)
        {
                for (unsigned j = ; j < (int)a[i].size(); j++)
                {
                        if (m >= i)
                        {
                                m -= i;
                                flg[a[i][j]] = false;
                        }
                }
        }
        int ans = ;
        for (int i = ; i <= n; i++)
                if (flg[i]) ans++;
        printf("Yes\n%d\n",ans);
        for (int i = ; i <= n; i++)
                if (flg[i]) printf("%d ",i);
        printf("\n");
 
        return ;
 
}