BZOJ3083: 遥远的国度(树链剖分)

题意

$n$个节点的树，每个点有权值，支持三种操作

1、 换根

2、把$x$到$y$路径上节点权值变为$z$

3、询问路径最小值

Sol

啥？你说这是TopTree的裸题？那你写去啊

很显然，如果没有第一个操作就是树剖的裸题

其实有了第一个操作也是树剖的裸题

我们考虑换根之后会对那些节点产生影响

以下图片来自(https://blog.csdn.net/lcomyn/article/details/45718295)

第一种情况：x == root

很显然直接查询子树的最小值就行

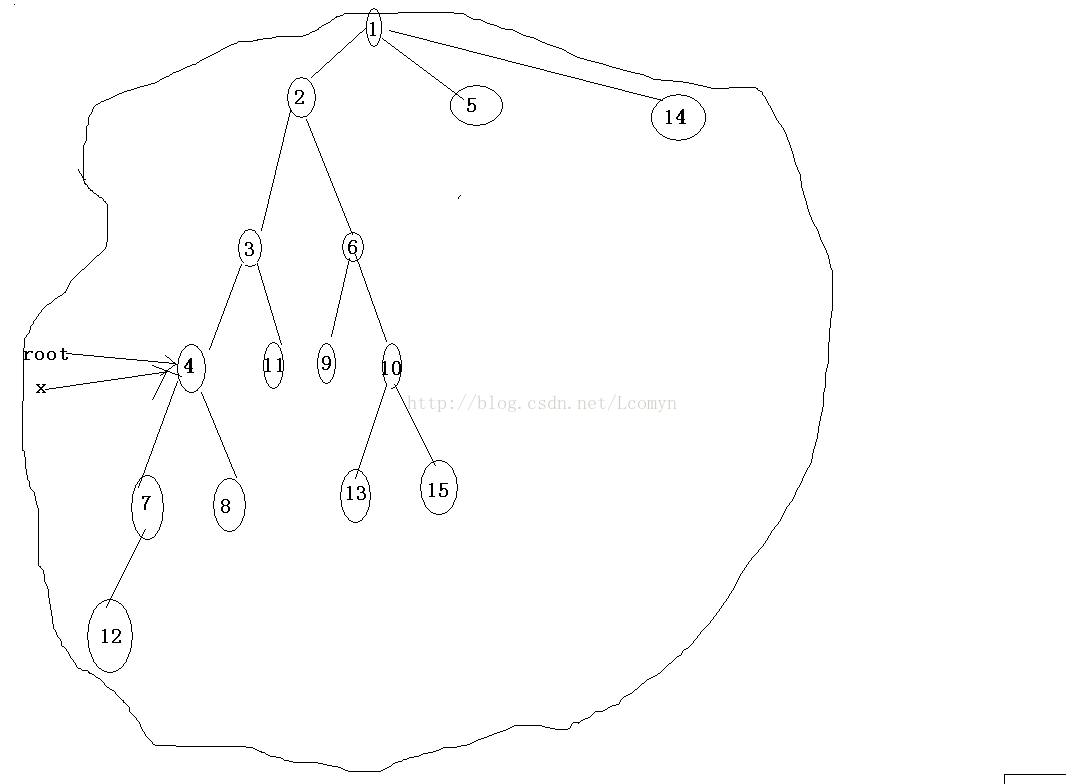
第二种情况：$lca(x,root) != x$

这种情况也简单，直接查询$x$子树中的最小值即可

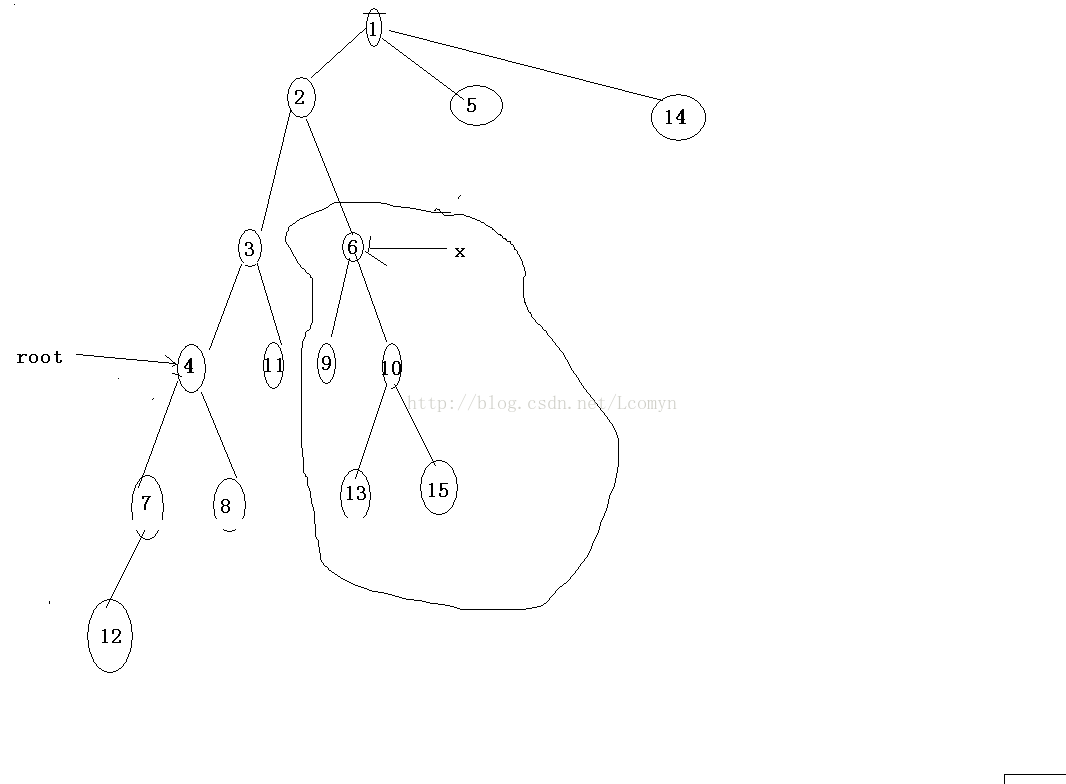
第三种情况：$lca(x,root) = x$

这种情况稍微复杂一些

我们需要找到$root$往上走，离$x$最近的点。

很显然，这个点以上的部分，就是我们要查询的区间

那么我们查询这个点的子树对应区间的补集即可

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN = 1e5 + , B = , INF = ;
inline int read() {
    char c = getchar(); int x = , f = ;
    while(c < '' || c > '') {if(c == '-') f = -; c = getchar();}
    while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
    return x * f;
}
int N, M, root = ;
int a[MAXN], b[MAXN];
vector<int> v[MAXN];
int fa[MAXN], top[MAXN], jump[MAXN][], deep[MAXN], siz[MAXN], l[MAXN], r[MAXN], tot = , cnt, son[MAXN], ID[MAXN];
void dfs1(int x, int _fa) {
    fa[x] = _fa; siz[x] = ; l[x] = ++cnt;
    jump[x][] = fa[x];
    for(int i = ; i < v[x].size(); i++) {
        int to = v[x][i];
        if(deep[to]) continue;
        deep[to] = deep[x] + ;
        dfs1(to, x);
        siz[x] += siz[to];
        if(siz[to] > siz[son[x]]) son[x] = to;
    }
    r[x] = cnt;
}
void dfs2(int x, int topf) {
    top[x] = topf; ID[x] = ++tot; a[tot] = b[x];
    l[x] = tot;
    if(!son[x]) {r[x] = tot; return ;}
    dfs2(son[x], topf);
    for(int i = ; i < v[x].size(); i++) {
        int to = v[x][i];
        if(top[to]) continue;
        dfs2(to, to);
    }
    r[x] = tot;
}
void Pre() {
    for(int i = ; i <= B; i++)
        for(int j = ; j <= N; j++)
            jump[j][i] = jump[jump[j][i - ]][i - ];
}
#define ls k << 1
#define rs k << 1 | 1
struct Node {
    int l, r, mi, si, tag;
}T[MAXN * ];
void update(int k) {T[k].mi = min(T[ls].mi, T[rs].mi);}
void ps(int k, int val) {T[k].mi = val; T[k].tag = val; return ;}
void pushdown(int k) {
    if(!T[k].tag) return;
    ps(ls, T[k].tag); ps(rs, T[k].tag);
    T[k].tag = ;
}
void Build(int k, int ll, int rr) {
    T[k].l = ll; T[k].r = rr; T[k].si = r - l + ;
    if(ll == rr) {T[k].mi = a[ll]; return ;}
    int mid = ll + rr >> ;
    Build(ls, ll, mid); Build(rs, mid + , rr);
    update(k);
}
void IntervalMem(int k, int ll, int rr, int val) {
    if(ll <= T[k].l && T[k].r <= rr) {
        T[k].mi = T[k].tag = val;
        return;
    }
    pushdown(k);
    int mid = T[k].l + T[k].r >> ;
    if(ll <= mid) IntervalMem(ls, ll, rr, val);
    if(rr >  mid) IntervalMem(rs, ll, rr, val);
    update(k);
}
void TreeChange(int x, int y, int val) {
    while(top[x] != top[y]) {
        if(deep[top[x]] < deep[top[y]]) swap(x, y);
        IntervalMem(, ID[top[x]], ID[x], val);
        x = fa[top[x]];
    }
    if(deep[x] < deep[y]) swap(x, y);
    IntervalMem(, ID[y], ID[x], val);
}
int IntervalMin(int k, int ll, int rr) {
    int ans = INF;
    if(ll <= T[k].l && T[k].r <= rr) return T[k].mi;
    pushdown(k);
    int mid = (T[k].l + T[k].r) >> ;
    if(ll <= mid) ans = min(ans, IntervalMin(ls, ll, rr));
    if(rr >  mid) ans = min(ans, IntervalMin(rs, ll, rr));
    return ans;
}
int LCA(int x, int y) {
    while(top[x] != top[y]) {
        if(deep[top[x]] < deep[top[y]]) swap(x, y);
        x = fa[top[x]];
    }
    if(deep[x] < deep[y]) swap(x, y);
    return y;
}
int Find(int rt, int x) {
    for(int i = B; i >= ; i--)
        while(deep[jump[rt][i]] > deep[x])
            rt = jump[rt][i];
    return rt;
}
int Query(int x) {
    if(x == root) return T[].mi;
    int lca = LCA(x, root);
    if(lca != x) return IntervalMin(, l[x], r[x]);
    int v = Find(root, x), ans = INF;
    if(l[v] > ) ans = min(ans, IntervalMin(, , l[v] - ));//tag
    if(r[v] < N) ans = min(ans, IntervalMin(, r[v] + , tot));
    return ans;
}
int main() {
    N = read(); M = read();
    for(int i = ; i <= N - ; i++) {
        int x = read(), y = read();
        v[x].push_back(y); v[y].push_back(x);
    }
    for(int i = ; i <= N; i++) b[i] = read();
    root = read();
    deep[] = ;
    dfs1(, );
    dfs2(, );
    Pre();
    Build(, , tot);
    while(M--) {
        int opt = read();
        if(opt == ) root = read();
        else if(opt == ){
            int x1 = read(), x2 = read(), v = read();
            TreeChange(x1, x2, v);
        } else {
            int x = read();
            printf("%d\n", Query(x));
        }
    }
    return ;
} 

/*
3 7
1 2
1 3
1 2 3
1
3 1
2 1 1 6
3 1
2 2 2 5
3 1
2 3 3 4
3 1
*/