YCOJ单向公路

题目：

描述

某地区有许多城镇，但并不是每个城镇都跟其他城镇有公路连接，并且有的公路并不能双向行驶。现在我们把这些城镇间的公路分布及允许的行驶方向告诉你，你需要编程解决通过公路是否可以从一个城镇到达另一个城镇。（我们规定，城镇自己跟自己可互相到达，即 a 可到达 a）。

输入

第一行只有一个数 N ，下面将跟着 2N 行数据。

在前 N 行数据中，每行数据开头第一个数字 number，表明这一行总共有 number个数， number的下一个数为 i ，代表编号为 i 的城镇。这行余下的就是跟 i 有公路连接的城镇名单，并且只能从城镇 i 驶向其他城镇。如 4 1 2 3，表明：此行有 4 个数，跟城镇 1 有公路连接的城镇是编号为 2 和 3 的城镇，且只允许从城镇 1驶向城镇 2 和 3 ，而不能从 2 到 1 或 3 到 1。

在后 N 行数据中,每行由两个数字组成 a , b。

对于每个输入的数有如下关系 0≤input_number≤1000。

输出

对于输入数据中的每个 a,b，判断是否可以从城镇 a 通过公路到达城镇 b，如果可以，输出 Yes；否则输出No。

输入样例 1

3
4 1 2 3
3 4 5
3 5 8
1 2
1 8
4 8

输出样例 1

Yes
No
Yes

这是一道经典的搜索题，用BFS或DFS都行，因为博主DFS打的已经很熟了，准备挑战一下自己，所以我就来讲讲BFS的做法。

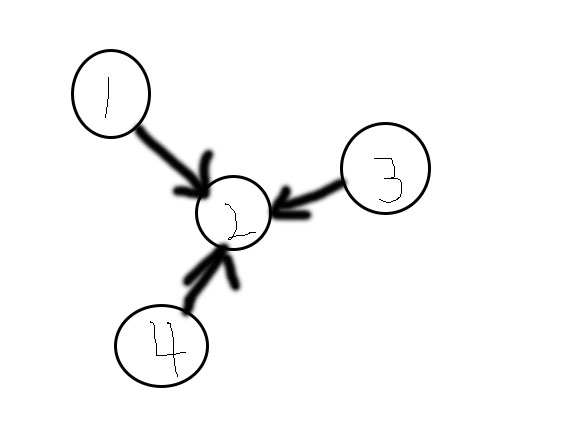
如图，因为是单向公路，所以尽管所有点都连得到点2，但点2却一个点都走不到，所以这是一个有向图。

---

首先，让我们来定义一波：

int n;
queue<int>q;
vector<int>g[];

这里也就不需要讲了吧，bfs必备的vector和queue的定义也就这样。

---

接下来，我们把输入输出解决了，这个输入特别怪异。输入n有2n行，前n行会首先输入一个number，代表这一行加上它共有number个数；后n行每行2个数，是询问，问a和b书否连通。

    cin>>n;
    for (int i=;i<=n;i++){
        int tmp1,tmp2;
        cin>>tmp1>>tmp2;
        for (int j=;j<tmp1-;j++){
            int x;
            cin>>x;
            g[tmp2].push_back(x);
        }

    }

然后进行输出，如果bool类型的bfs值是true或a和b相等，就输出Yes，否则输出No。

    for (int i=;i<=n;i++){
        int a,b;
        cin>>a>>b;
        if(bfs(a,b)==true||a==b){
            cout<<"Yes"<<endl;
        }
        else {
            cout<<"No"<<endl;
        }
    }

---

最后，开始我们的BFS！

首先，把起点push到队列里。

bool bfs(int start,int end){
    q.push(start);
}

然后开始BFS套路：while (!q.empty())

接下来，将目前的位置取出来(now)，再弹出队列。

最后，遍历g[now]，如果到达了end，就返回ture，否则就将找到的点放在队列里。如果队列都已经清空了，那就只有遗憾地告诉你，没有找到。只有输出No了。

整个BFS：

bool bfs(int start,int end){

    q.push(start);
    while (!q.empty()){
        int now=q.front();
        q.pop();
        for (int i=;i<g[now].size();i++){
            if(g[now][i]==end){
                return true;
            }
            q.push(g[now][i]);
        }
    }
    return false;
}

---

完整代码：

#include <bits/stdc++.h>
using namespace std;
int n,vis[];
queue<int>q;
vector<int>g[];

bool bfs(int start,int end){

    q.push(start);
    while (!q.empty()){
        int now=q.front();
        q.pop();
        for (int i=;i<g[now].size();i++){
            if(g[now][i]==end){
                return true;
            }
            q.push(g[now][i]);
        }
    }
    return false;
}

int main(){
    cin>>n;
    for (int i=;i<=n;i++){
        int tmp1,tmp2;
        cin>>tmp1>>tmp2;
        for (int j=;j<tmp1-;j++){
            int x;
            cin>>x;
            g[tmp2].push_back(x);
        }

    }
    for (int i=;i<=n;i++){
        int a,b;
        cin>>a>>b;
        if(bfs(a,b)==true||a==b){
            cout<<"Yes"<<endl;
        }
        else {
            cout<<"No"<<endl;
        }
    }
    return ;
}

最后，Accept送给大家！