bzoj 4037: [HAOI2015]数字串拆分【dp+矩阵加速】

首先f长得就很像能矩阵优化的，先构造转移矩阵（这里有一点神奇的地方，我看网上的blog和我构造的矩阵完全不一样还以为我的构造能力又丧失了，后来惊奇的发现我把那篇blog里的构造矩阵部分换成我的构造方式，交了一下完全没问题2333，并不知道为啥）

好久没写矩阵加速了，顺便说一下我的构造方法吧：

首先明确转移矩阵的目的，设m为构成f[i]的最小项f[i-m]，也就是f[i]=f[i-m]+f[i-...]+f[i-...]+....，其中i-m是最小的。我们需要构造一个m大小的矩阵，使得{f[i-m],f[i-m+1].....f[i-1}乘上这个正方形矩阵变成{f[i-m+1],f[i-m+2]....f[i]}然后因为矩阵乘法是一行乘一列，所以每个右边的每个f[i]都对应了一行矩阵和左边的每项依次相乘。拿这道题的递推式，m=3为例：



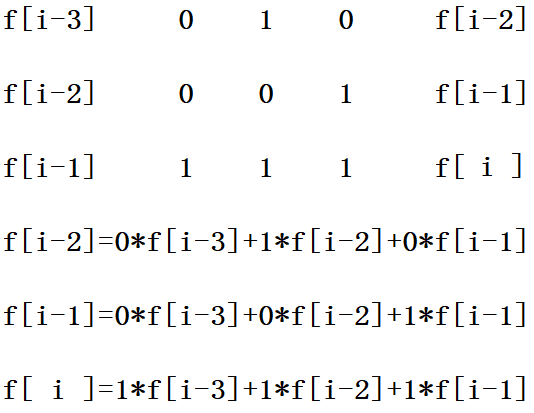
以上，我也不知道我在说什么。

然后这道题的精髓在于它使用f的矩阵进行g的dp。设f[i]为前i位的答案，因为矩阵乘法的结合律，我们可以记\( g[i]=\sum_{j=1}^{m}g[j]*c[j+1][i] \)。然后考虑如何预处理出c，可以设c[i][j]为i这个数(1<=i<=9)的\( j^{10} \)次（假装高精）。

总之，一道好题。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=505,mod=998244353;
int n,m;
char s[N];
struct qwe
{
	int a[7][7];
	void init()
	{
		memset(a,0,sizeof(a));
	}
	void pre()
	{
		memset(a,0,sizeof(a));
		for(int i=1;i<=m;i++)
			a[i][i]=1;
	}
	qwe operator * (const qwe &b) const
	{
		qwe c;
		c.init();
		for(int k=1;k<=m;k++)
			for(int i=1;i<=m;i++)
				for(int j=1;j<=m;j++)
					c.a[i][j]=(c.a[i][j]+1ll*a[i][k]*b.a[k][j]%mod)%mod;
		return c;
	}
	qwe operator + (const qwe &b) const
	{
		qwe c;
		c.init();
		for(int i=1;i<=m;i++)
			for(int j=1;j<=m;j++)
				c.a[i][j]=(b.a[i][j]+a[i][j])%mod;
		return c;
	}
}f[N],a,c[15][N];
qwe ksm(qwe a,int b)
{
	qwe r;
	r.pre();
	while(b)
	{
		if(b&1)
			r=r*a;
		a=a*a;
		b>>=1;
	}
	return r;
}
int main()
{
	scanf("%s%d",s+1,&m);
	n=strlen(s+1);
	for(int i=1;i<=n;i++)
		s[i]-='0';
	for(int i=1;i<m;i++)
		a.a[i][i+1]=1;
	for(int i=1;i<=m;i++)
		a.a[m][i]=1;
	c[0][1].pre();
	for(int i=1;i<=9;i++)
	{
		c[i][1]=c[i-1][1]*a;
		for(int j=2;j<=n;j++)
			c[i][j]=ksm(c[i][j-1],10);
	}
	f[0].a[1][m]=1;
	for(int i=1;i<=n;i++)
	{
		qwe tmp=c[s[i]][1];
		for(int j=i-1;j>=0;j--)
		{
			f[i]=f[i]+f[j]*tmp;
			if(j&&s[j])
				tmp=tmp*c[s[j]][i-j+1];
		}
	}
	printf("%d\n",f[n].a[1][m]);
	return 0;
}