Hdu1401-Solitaire(双向bfs)

Solitaire is a game played on a chessboard 8x8. The rows and columns of the chessboard are numbered from 1 to 8, from the top to the bottom and from left to right respectively.
There are four identical pieces on the board. In one move it is allowed to:
> move a piece to an empty neighboring field (up, down, left or right),
> jump over one neighboring piece to an empty field (up, down, left or right).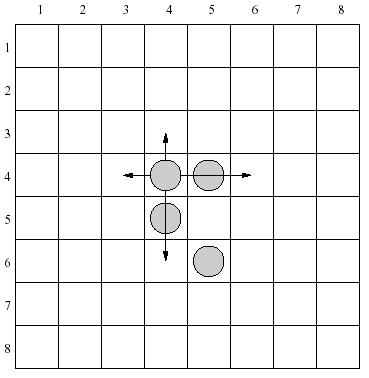There are 4 moves allowed for each piece in the configuration shown above. As an example let's consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right.
Write a program that:
> reads two chessboard configurations from the standard input,
> verifies whether the second one is reachable from the first one in at most 8 moves,
> writes the result to the standard output.

 

Input

Each of two input lines contains 8 integers a1, a2, ..., a8 separated by single spaces and describes one configuration of pieces on the chessboard. Integers a2j-1 and a2j (1 <= j <= 4) describe the position of one piece - the row number and the column number respectively. Process to the end of file.

 

Output

The output should contain one word for each test case - YES if a configuration described in the second input line is reachable from the configuration described in the first input line in at most 8 moves, or one word NO otherwise.

 

Sample Input

4 4 4 5 5 4 6 5

2 4 3 3 3 6 4 6

 

Sample Output

YES

 

题意：棋盘大小为8*8，然后有4个球，给出初始所有球的位置以及目标位置，每次可以移动一个球，要么移动到旁边空的地方，要么跨过一个

球到空的地方（不能跨过多个球），问能否在8步以内到达目标状态。

 

解析：限定了8步，而且前后搜效果是一样的，所以可以考虑用双向bfs，然后8个数哈希，要注意对4个点要排序。

 

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int mod=;
const int maxn=;
int dx[]={-,,,},dy[]={,-,,};
bool in(int x,int y){ return x>=&&x<=&&y>=&&y<=; }
struct point   //球的坐标
{
    int x,y;
    point(int x=,int y=):x(x),y(y){}
    bool operator < (const point& t) const
    {
        if(x!=t.x) return x<t.x;
        return y<t.y;
    }
};
struct node
{
    point p[];  //每个节点保存4个球的坐标，并且是排好序的
}nod[][maxn];   //开二维用于双向搜
struct Hash
{
    int v,k,nid,next;   //保存哈希值，0或1，下标，next指针
}ha[mod+maxn];
int f[],r[],hash_id;  //队首队尾指针
bool Same(int k1,int a,int k2,int b)  //判断两个结构体是否完全相同
{
    for(int i=;i<;i++)
    {
        if(nod[k1][a].p[i].x!=nod[k2][b].p[i].x) return false;
        if(nod[k1][a].p[i].y!=nod[k2][b].p[i].y) return false;
    }
    return true;
}
int GetHash(point p[])  //得到哈希值
{
    int ret=,k=;
    for(int i=;i<;i++)
    {
        ret+=p[i].x*k; k*=;  //k是系数
        ret+=p[i].y*k; k*=;
    }
    return ret;
}
int Insert_Hash(int v,int k,int nid)  //插入
{
    int a=v%mod;
    int p=ha[a].next;
    while(p!=-)
    {
        if(ha[p].v==v&&Same(ha[p].k,ha[p].nid,k,nid)) return ha[p].k==k?:;  //有相同的状态，k值相同返回0，不同返回1
        p=ha[p].next;
    }
    p=++hash_id;
    ha[p].v=v; ha[p].k=k; ha[p].nid=nid;  //增加新的节点
    ha[p].next=ha[a].next; ha[a].next=p;
    return -;
}
bool Has(node& t,int x,int y)
{
    for(int i=;i<;i++) if(t.p[i].x==x&&t.p[i].y==y) return true;  //此处是球
    return false;
}
bool AddNode(node& t,int i,int j,int k)
{
    int x=t.p[i].x;
    int y=t.p[i].y;
    int nx=x+dx[j];
    int ny=y+dy[j];
    if(!in(nx,ny)) return false;   //出界
    if(Has(t,nx,ny)) nx+=dx[j],ny+=dy[j]; //有球
    if(!in(nx,ny)) return false;  //出界
    if(Has(t,nx,ny)) return false; //还有球
    node& tt=nod[k][r[k]];
    tt=t;
    tt.p[i].x=nx; tt.p[i].y=ny;
    sort(tt.p,tt.p+);   //排序
    int a=Insert_Hash(GetHash(tt.p),k,r[k]);
    if(a==) return true;  //找到解
    else if(a==-) r[k]++;  //增加新节点
    return false;
}
bool bfs(int k)
{
    int en=r[k];
    while(f[k]<en)
    {
        node& t=nod[k][f[k]++];
        for(int i=;i<;i++)   //4个球4个方向
            for(int j=;j<;j++) if(AddNode(t,i,j,k)) return true;
    }
    return false;
}
bool solve()
{
    if(Same(,,,)) return true;  //相同
    int step=;
    f[]=f[]=; r[]=r[]=;
    for(int i=;i<mod;i++) ha[i].next=-;
    hash_id=mod-;
    Insert_Hash(GetHash(nod[][].p),,);
    Insert_Hash(GetHash(nod[][].p),,);
    while(f[]<r[]||f[]<r[])
    {
        if(step>=) return false;
        step++;
        if(bfs()) return true;
        if(bfs()) return true;
    }
    return false;
}
int main()
{
    int x,y;
    while(scanf("%d%d",&x,&y)!=EOF)
    {
        nod[][].p[]=point(x,y);
        for(int i=;i<;i++)
        {
             scanf("%d%d",&x,&y);
             nod[][].p[i]=point(x,y);
        }
        for(int i=;i<;i++)
        {
             scanf("%d%d",&x,&y);
             nod[][].p[i]=point(x,y);
        }
        sort(nod[][].p,nod[][].p+);
        sort(nod[][].p,nod[][].p+);
        if(solve()) printf("YES\n");
        else printf("NO\n");
    }
    return ;
}