hdu3095-Eleven puzzle(双向搜索+哈希)

Partychen invents a new game named “Eleven Puzzle” .Just like the classic game “Eight Puzzle”,but there some difference between them:The shape of the board is different and there are two empty tiles. 

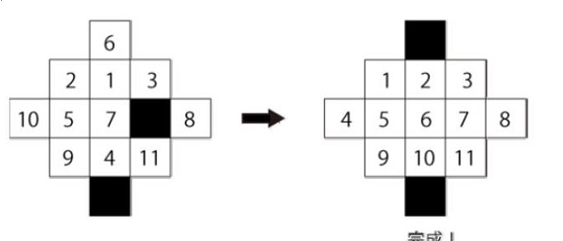
The tile in black means it’s empty

Each step you can move only one tile. 
Here comes the problem.How many steps at least it required to done the game. 

 

Input

The first line of input contains one integer specifying the number of test cases to follow. 
Every case contains five lines to describe the initial status of the board. 0 means empty.

It’s confirmed that the board is legal.

 

Output

Output one line for each testcase.Contain an integer denotes the minimum step(s) it need to complete the game.Or “No solution!” if it’s impossible to complete the game within 20 steps.

 

Sample Input

3

2

1 0 3

4 5 6 7 8

9 0 11

10

0

1 2 3

4 5 6 7 8

9 10 11

0

0

11 10 9

8 7 6 5 4

3 2 1

0

 

Sample Output

2

0

No solution!

 

题意：给出上图的11数码，有2个空格，每次可以移一步，问能否在20步以内达到目标状态，如果能输出步数，否则输出No solution!

 

解析：题目给了20步的限制，而且前后搜效果是一样的，所以很容易想到双向bfs，但是状态怎么保存呢，有11个数外加2个空格，可以考虑用康拓展开，但不能用数组保存值，因为值太大了，所以可以考虑用map，我用的方法是哈希，给每个数乘上一个权值，然后加起来哈希成一个值，用数组模拟链表保存状态，但可能出现两种不同的状态哈希成同一个值，所以在相同的情况下还要整个进行对比。

 

源代码

#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
#include<sstream>
#include<algorithm>
#include<utility>
#include<vector>
#include<set>
#include<map>
#include<queue>
#include<cmath>
#include<iterator>
#include<stack>
using namespace std;
const int INF=1e9+;
const double eps=1e-;
const int mod=;
const int maxn=;
int f[],r[];   //双向bfs的两个队列的队首队尾指针
int dx[]={-,,,},dy[]={,-,,}; //方向数组
bool in(int x,int y){ return x>=&&x<&&y>=&&y<; } //是否越界
struct node
{
    int px[],py[];  //保存2个空格的位置和整个数组
    int A[][];
}nod[][maxn];  //0是前面搜，1是后面搜
int B[][]={   //最终状态
    -,-,,-,-,
    -,,,,-,
    ,,,,,
    -,,,,-,
    -,-,,-,-
};
bool Same(int A[][])  //判断该状态是否与最终的状态相等
{
    for(int i=;i<;i++)
        for(int j=;j<;j++)
        if(A[i][j]!=B[i][j]) return false;
    return true;
}
int F[];  //保存2^i
void GetF()
{
    F[]=;
    for(int i=;i<;i++) F[i]=F[i-]*;
}
int Get(int A[][])  //得到哈希值
{
    int ret=,k=;
    for(int i=;i<;i++)
        for(int j=;j<;j++) if(A[i][j]>) ret+=F[k++]*A[i][j]; //乘上一个权值
    return ret;
}
struct Hash
{
    int v,next,nid,k;   //是哈希值，next指向下一个节点，nid和k分别保存是下标和0或1
}ha[mod+maxn];
int hash_id;
bool check(int a,int k1,int b,int k2)  //判断是否完全相等
{
    for(int i=;i<;i++)
        for(int j=;j<;j++)
        if(nod[k1][a].A[i][j]!=nod[k2][b].A[i][j]) return false;
    return true;
}
int Insert_Hash(int v,int nid,int k)  //插入
{
    int a=v%mod;
    int p=ha[a].next;
    while(p!=-)
    {
        if(ha[p].v==v&&check(ha[p].nid,ha[p].k,nid,k)) return ha[p].k;//有相同的状态
        p=ha[p].next;
    }
    p=++hash_id;  //没有则增加新节点，前插法
    ha[p].v=v; ha[p].nid=nid; ha[p].k=k;
    ha[p].next=ha[a].next; ha[a].next=p;
    return -;   //-1代表插入了新节点
}
bool AddNode(node& t,int i,int j,int k)
{
    int x=t.px[i],y=t.py[i];
    int nx=x+dx[j],ny=y+dy[j];
    if(!in(nx,ny)||t.A[nx][ny]<=) return false;
    node& tt=nod[k][r[k]];
    tt=t;
    swap(tt.A[x][y],tt.A[nx][ny]);  //交换
    tt.px[i]=nx; tt.py[i]=ny;
    int a=Insert_Hash(Get(tt.A),r[k],k);
    if(a==-){ r[k]++; return false; } //队尾指加1
    else if(a==k) return false;   //自己原来访问过的状态
    else return true;    //相遇了，找到了解
}
void Print(node& t)
{
    for(int i=;i<;i++)
    {
        for(int j=;j<;j++) printf("%d ",t.A[i][j]);
        puts("");
    }
    puts("=========");
    getchar();
}
bool bfs(int k)
{
    int& be=f[k];
    int en=r[k];
    while(be<en)
    {
        node& t=nod[k][be++];
        //Print(t);
        for(int i=;i<;i++)
            for(int j=;j<;j++) if(AddNode(t,i,j,k)) return true;
    }
    return false;
}
int solve()
{
    if(Same(nod[][].A)) return ;
    for(int i=;i<;i++)
        for(int j=;j<;j++) nod[][].A[i][j]=B[i][j];  //最终状态
    nod[][].px[]=; nod[][].py[]=;
    nod[][].px[]=; nod[][].py[]=;
    int step=;
    f[]=f[]=,r[]=r[]=;
    for(int i=;i<mod;i++) ha[i].next=-;
    hash_id=mod-;
    while(f[]<r[]||f[]<r[]) //双向搜
    {
        step++;
        if(bfs()) return step;
        step++;
        if(bfs()) return step;
        if(step>=) return -;
    }
    return -;
}
int main()
{
    int T;
    GetF();
    scanf("%d",&T);
    while(T--)
    {
        int k=;
        for(int i=;i<;i++)
            for(int j=;j<;j++)//得到初始状态
        {
            if(B[i][j]==-) { nod[][].A[i][j]=-; continue; }
            scanf("%d",&nod[][].A[i][j]);
            if(nod[][].A[i][j]==)
                { nod[][].px[k]=i; nod[][].py[k++]=j; }
        }
        int ans=solve();
        if(ans==-) printf("No solution!\n");
        else printf("%d\n",ans);
    }
    return ;
}