cf444A DZY Loves Physics

A. DZY Loves Physics

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

DZY loves Physics, and he enjoys calculating density.

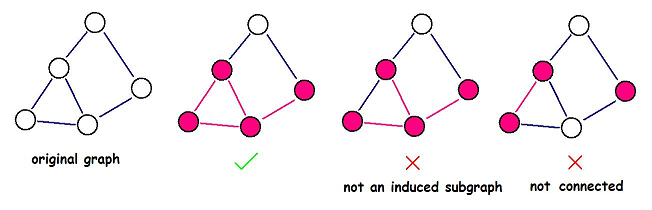
Almost everything has density, even a graph. We define the density of a non-directed graph (nodes and edges of the graph have some values) as follows:

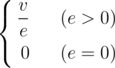
where v is the sum of the values of the nodes, e is
the sum of the values of the edges.

Once DZY got a graph G, now he wants to find a connected induced subgraph G' of
the graph, such that the density of G' is as large as possible.

An induced subgraph G'(V', E') of a graph G(V, E) is
a graph that satisfies:

• ;
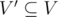• edge 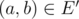 if
  and only if ,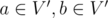
  and edge ;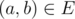
• the value of an edge in G' is the same as the value of the corresponding edge in G,
  so as the value of a node.

Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected.

Input

The first line contains two space-separated integers n (1 ≤ n ≤ 500), .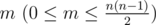
Integer n represents the number of nodes of the graph G, m represents
the number of edges.

The second line contains n space-separated integers xi (1 ≤ xi ≤ 106),
where xi represents
the value of the i-th node. Consider the graph nodes are numbered from 1 to n.

Each of the next m lines contains three space-separated integers ai, bi, ci (1 ≤ ai < bi ≤ n; 1 ≤ ci ≤ 103),
denoting an edge between node ai and bi with
value ci. The
graph won't contain multiple edges.

Output

Output a real number denoting the answer, with an absolute or relative error of at most 10 - 9.

Sample test(s)

input

1 0
1

output

0.000000000000000

input

2 1
1 2
1 2 1

output

3.000000000000000

input

5 6
13 56 73 98 17
1 2 56
1 3 29
1 4 42
2 3 95
2 4 88
3 4 63

output

2.965517241379311

Note

In the first sample, you can only choose an empty subgraph, or the subgraph containing only node 1.

In the second sample, choosing the whole graph is optimal.

lwh大神说，这不是01分数规划吗，二分+网络流！

我吓坏了

结果事实证明ccr代码竟然真A了

贪心证明略（废话我当然不知道怎么证）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
using namespace std;
int x[1000001];
int main()
{
int n, m;
cin >> n >> m;
double ans = 0;
int p, q, c;
for (int i = 1; i<= n; i++)
cin >> x[i];
for (int i = 0; i< m; i++)
{
cin >> p >> q >> c;
ans = max(ans, (double) (x[p] + x[q]) / c);
}
printf("%.10f", ans);
}