[bzoj 2460]线性基+贪心+证明过程

题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=2460

网上很多题目都没说这个题目的证明，只说了贪心策略，我比较愚钝，在大神眼里的显然的策略还是想证明一下才安心……所以这里记录一下证明过程。

贪心策略：按魔力值从大到小排序，从大往小往线性基里插，如果成功插入新元素，就选这个，如果插不进去，就不选这个。

证明：

　　设有n个材料，每个材料的属性值是x[1],x[2],...,x[n]，魔力值是v[1],v[2],...,v[n]，这里假设v已经排好序，即v[1]>=v[2]>=v[3]>=...>=v[n]。

　　首先证，一定有一个最优解，包含材料1，其属性值是x[1]，魔力值是v[1]。

　　　　假设原问题存在一个最优解 S = { t₁, t₂, ... , t_k }。其中t_i代表第t_i个物品，且t1<t2<...<tk。

　　　　　　如果t1等于1，那么得证。

　　　　　　如果t1不等于1，那么我们来证一定有一个元素可以被1替换下来。

　　　　　　　　考虑1为何不能加进S。因为S是线性无关的，加入1以后，S∪{1}就变得线性相关了。所以必然存在S的一个子集，它们的异或和等于x[1]。

　　　　　　　　用表达式写出来也就是

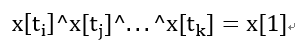(1)

　　　　　　　　那么1可以把谁替换下来呢？答案是1可以把任何一个替换下来。我们不妨让它替换下来ti，把式子变一下形，两边同时异或上x[ti]^x[1]，就得到了

(2)

　　　　　　　　就会发现x[ti]已经可以被线性表示出来了，而且显然，如果不加x[1]肯定是无法线性表示出来x[ti]的（因为S是线性无关的），所以替换后的线性基跟原来是等价的。

　　　　　　　　如果不放心，我可以再重述一遍，对于原来S可以表示出来的，替换后的一定也可以表示出来，因为被替换掉的x[ti]已经可以表示出来了；对于原来S不能表示出来的，替换后的也一定表示不出来。可以用反证法证。假设有一个y，用原来的表示不出来，而用替换后的可以表示出来。那肯定是因为加入了x[1]的原因。用式子写出来就是：

(3)

　　　　　　　　把x[1]用(1)式代换，就可以得到：

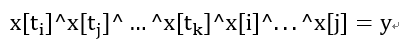(4)

　　　　　　　　是不是担心，万一左边的x都抵消没了怎么办？实际上不会出现这种情况，因为ti就是独一无二的，在x[i]^...^x[j]里是不会有的（因为ti已经被1替换下来了）。这样，就得到了原来的基也可以得到y，与假设矛盾。

　　所以这一步证明的作用是什么呢？就是证明了，第一步的贪心策略是正确的。下面来证明，如果第一步的贪心是正确的，以后的贪心也是正确的。

　　现在只需证，假设当前已经按照贪心策略造出了一个线性无关的基S = { t₁, t₂, ... , t_k }，一定存在一个最优解，包含下一步选择的那个最大魔力值的跟S线性无关的一个材料。

　　设下一步的贪心策略选择是j，假设最优解是 G = {t₁, t₂, ... , t_k , t_k+1, t_k+2, ... , t_k+m}。

　　　　如果j∈G，那么得证。

　　　　如果j∉G，现在证j一定可以替换掉G中的某个元素，实际上j可以替换掉跟它线性相关的那些元素里的任何一个元素，证明方法跟第一步类似。

　　　　　　j为什么不能属于G呢？因为G是线性无关的，但是加入j之后，就线性相关了，也就是说j是多余的，j可以用其他的线性表示出来。那么可以得到的式子就是：

(5)

（补充：图片里的i, j, k都是代指任意变量）

　　　　这个式子实际上跟(1)式是一模一样的。而且这里的i肯定>k，因为根据已知的策略，j一定会选跟t1...tk线性无关的最前面的那个。那么到此，后面的证明跟第1步的证明也是类似的，j也可以替换掉任何一个ti (i>k)。

　　综上，问题得证。

代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

const int maxn=;
pair<int,ll> a[maxn];

vector<ll> base;
bool add(ll x)
{
    for(int i=;i<base.size();i++)
        x=min(x,x^base[i]);
    if (x) base.push_back(x);
    if (x) return true;
    else return false;
}

int main()
{
    int n;
    scanf("%d",&n);
    for (int i=;i<n;i++) scanf("%lld%d",&a[i].second,&a[i].first);
    sort(a,a+n);
    int ans=;
    for (int i=n-;i>=;i--) if (add(a[i].second)) ans+=a[i].first;
    printf("%d",ans);
    return ;
}