poj1179 Polygon【区间DP】

Polygon

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions:6633		Accepted: 2834

Description

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N. 

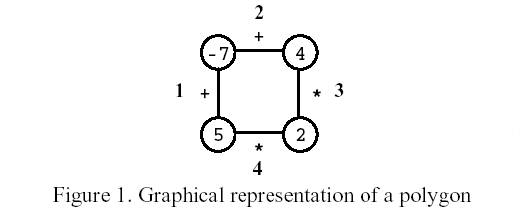
On the first move, one of the edges is removed. Subsequent moves involve the following steps: 
�pick an edge E and the two vertices V1 and V2 that are linked by E; and 
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2. 
The game ends when there are no more edges, and its score is the label of the single vertex remaining.

Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.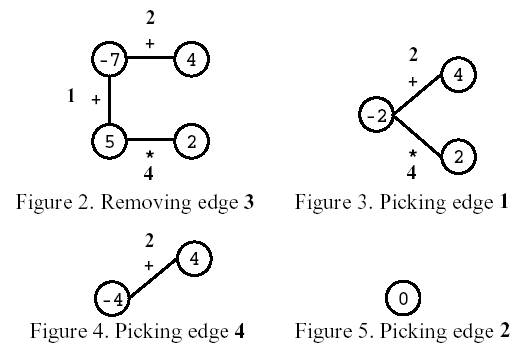 

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score. 

Input

Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices' labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *).

3 <= N <= 50 
For any sequence of moves, vertex labels are in the range [-32768,32767]. 

Output

Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

Source

IOI 1998

题意：

给一个n个顶点n条边的多边形，顶点上有一个整数值，边上有一个字符表示+ 或者 *。首先删除一条边，然后每次对两个顶点进行合并，用一个顶点代替这两个顶点，顶点的值是这两个顶点运算的结果，运算符为连接这两个顶点的边。最后只剩下一个顶点，问这个顶点最大值会是多少，以及得到这个结果的删边方法。

思路：

删除了一条边后，就类似于石子合并（https://www.cnblogs.com/wyboooo/p/9757387.html）这道题了。

不同之处在于因为有负数和乘法的存在，最大值有可能是由两个最小值相乘得到的。因此需要同时记录最大值和最小值。【已经遇到好多有负数、乘法要记录最大值最小值的问题了，需要注意！】

最开始需要枚举删掉的边，一个好方法是，将原来的数组在末尾复制一遍。从1~n跑一遍成为枚举，最后找dp[i][i+n-1]的最大值就行了。

这种“任意选择一个位置断开，复制形成2倍长度的链”的方法，是解决DP中环形结构的常用手段之一。

 //#include <bits/stdc++.h>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<stdio.h>
 #include<cstring>
 #include<map>

 #define inf 0x3f3f3f3f
 using namespace std;
 typedef long long LL;

 int n;
 const int maxn = ;
 int num[maxn * ];
 char op[maxn * ];
 int dp[maxn * ][maxn * ][];

 int main()
 {
     while(scanf("%d", &n) != EOF){

         for(int i = ; i <= n; i++){
             scanf(" %c %d", &op[i], &num[i]);
         }
         for(int i = n + ; i <=  * n; i++){
             op[i] = op[i - n];
             num[i] = num[i - n];
         }
         for(int i = ; i <= n * ; i++){
             dp[i][i][] = dp[i][i][] = num[i];
             for(int j = i + ; j <=  * n; j++){
                 dp[i][j][] = -inf;
                 dp[i][j][] = inf;
             }
         }

         for(int len = ; len <= n; len++){
             for(int l = ; l <=  * n - len + ; l++){
                 int r = l + len - ;
                 for(int k = l; k < r; k++){

                     int res1, res2;
                     if(op[k + ] == 't'){
                         res1 = dp[l][k][] + dp[k + ][r][];
                         res2 = dp[l][k][] + dp[k + ][r][];
                     }
                     else{
                         res1 = dp[l][k][] * dp[k + ][r][];
                         res2 = dp[l][k][] * dp[k + ][r][];
                         dp[l][r][] = max(dp[l][r][], dp[l][k][] * dp[k + ][r][]);
                         dp[l][r][] = min(dp[l][r][], dp[l][k][] * dp[k + ][r][]);
                         dp[l][r][] = min(dp[l][r][], dp[l][k][] * dp[k + ][r][]);
                     }
                     dp[l][r][] = max(dp[l][r][], res1);
                     dp[l][r][] = min(dp[l][r][], res2);
                 }
             }
         }

         int ans = -inf;
         for(int i = ; i <= n; i++){
             ans = max(dp[i][i + n - ][], ans);
         }
         printf("%d\n", ans);
         bool flag = false;
         for(int i = ; i <= n; i++){
             if(dp[i][i + n - ][] != ans)continue;
             if(flag){
                 printf(" ");
             }
             else{
                 flag = true;
             }
             printf("%d", i);
         }
         printf("\n");
     }
     return ;
 }