K倍区间 蓝桥杯

问题描述
　　给定一个长度为N的数列，A1, A2, ... AN，如果其中一段连续的子序列Ai, Ai+1, ... Aj(i <= j)之和是K的倍数，我们就称这个区间[i, j]是K倍区间。

　　你能求出数列中总共有多少个K倍区间吗？
输入格式
　　第一行包含两个整数N和K。(1 <= N, K <= 100000)
　　以下N行每行包含一个整数Ai。(1 <= Ai <= 100000)
输出格式
　　输出一个整数，代表K倍区间的数目。
样例输入
5 2
1
2
3
4
5
样例输出
6
数据规模和约定
　　峰值内存消耗（含虚拟机） < 256M
　　CPU消耗 < 2000ms

　　请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

　　注意：
　　main函数需要返回0;
　　只使用ANSI C/ANSI C++ 标准;
　　不要调用依赖于编译环境或操作系统的特殊函数。
　　所有依赖的函数必须明确地在源文件中 #include <xxx>
　　不能通过工程设置而省略常用头文件。

　　提交程序时，注意选择所期望的语言类型和编译器类型。

枚举所有区间和，然后一一判断是否可以整除K。

区间包含的元素可以有1/2/3/4……个，包含N个元素的区间和可以在包含N-1个元素的区间和的基础上加上元素N。

通过这样的反复迭代，可以求出所有的区间和。

可是OJ只给了25分，CPU和内存都超过了限制。

import java.util.Scanner;

public class Main {

    static int N;
    static int K;
    static int arr[];
    static int dp[][];
    static int result=0;

    static boolean judge(int a){
        if(a%K==0){
            return true;
        }
        return false;
    }

    public static void main(String[] args){
        Scanner reader=new Scanner(System.in);
        N=reader.nextInt();
        K=reader.nextInt();
        arr=new int[N+1];
        dp=new int[N+1][N+1];
        for(int i=1;i<=N;i++){
            arr[i]=reader.nextInt();
            dp[i][i]=arr[i];
            if(judge(dp[i][i])){
                result++;
            }
        }
        int count=1;
        while(count<=N-1){
            for(int i=1;i<=N-count;i++){
                dp[i][i+count]=dp[i][i+count-1]+arr[i+count];
                if(judge(dp[i][i+count])){
                    result++;
                }
            }
            count++;
        }
        System.out.print(result);
    }
}

参考了许多人的博客，思路大都一致。

求区间 [ i , j ] 的区间和，等于 [ 1 , j ] 的区间和减去 [ 1 , i-1 ]的区间和，用 sum[j]-sum[i-1] 来表示；

当区间和对K取模等于0即 ( sum[j]-sum[i-1] )%K= 0 (  化为sum[j]%K=sum[i-1] %K )  时此区间满足条件要求。

所以对每个sum[i]，求其值时顺求其对K的取模，最后得到一模数列，方便计算。

得到模数列，需选取模数列中的相同模进行组合，但题目限制了时空复杂度，此行不可行。

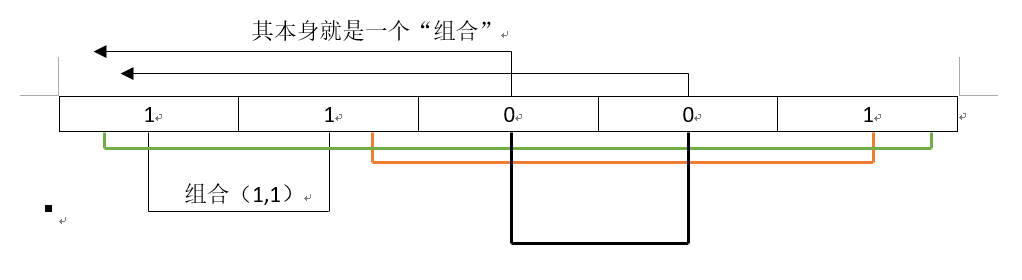
以题目中的第一个测试用例为例，求得模数列为 1 1 0 0 1

手动组合体验一下组合过程：

首元素 1 本身组合不了

第二个 1 可以与前面一个 1 组合

第三个元素 0 本身组合不了

第四个元素 0 可以与第三个元素 0 组合

第五个元素 1 可以与前面两个1 组合两次。（可以看出只要迭代加上前面已经出现过的相同模即可，假如存在第六个元素 1 ，此时它前面有 3 个 模 1 ，它可以与他们3个一一组合，一共在3种情况，所以加上3即可）

注意：模为0的情况，其本身不需要和其他0进行组合，因为他们不用和其他模相等（相减），自己这个数列本身就满足K倍。

Accept 代码

import java.util.Scanner;

public class Main {

    static int N;
    static int K;
    static int sum[];
    static int mod[];
    static long result=0;

    public static void main(String[] args){
        Scanner reader=new Scanner(System.in);
        N=reader.nextInt();
        K=reader.nextInt();
        sum=new int[N+1];
        mod=new int[K];
        for(int i=1;i<=N;i++){
            sum[i]=(sum[i-1]+reader.nextInt())%K;    //再次得到一个模 sum[i]
            result+=mod[sum[i]];    //其与前面相同的模一一组合
            mod[sum[i]]++;
        }
        System.out.print(result+mod[0]);
    }
}