Win32非递归遍历和搜索文件以及目录算法

转载请注明来源：http://www.cnblogs.com/xuesongshu

要点：

1、搜索的顶层目录在进入循环之前进栈

2、栈元素存储字符串指针，出栈时释放资源

3、每次循环开始，栈顶元素出栈

4、在遍历一个文件夹时，遇到子文件夹则进栈

5、外层循环以堆栈是否为空为标志，内层循环以FindNextFile返回值为标志

6、本搜索算法适用于按关键字搜索，当文件夹名称符合搜索条件时文件夹作为搜索结果通知调用者，不会入栈。

7、回调函数地址使用long型传递

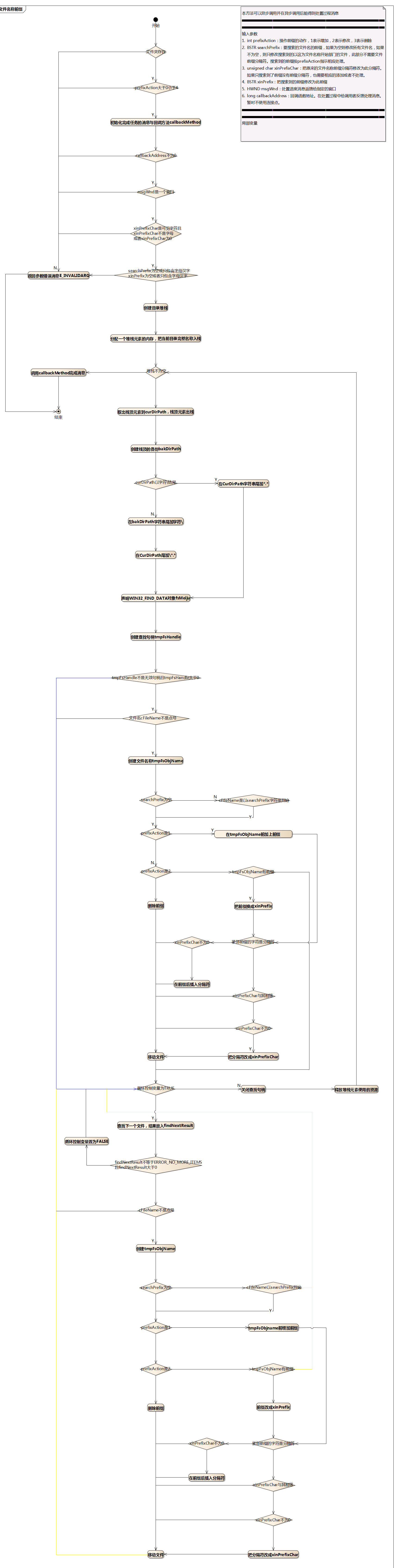
8、本程序功能是批量增加、修改或者删除指定文件夹下所有文件前缀，附带遍历功能。在参照流程图编写实现代码时与流程图所画逻辑会稍有出入。

流程图如下：

需要引入的头文件：

#include <stack>
#include <iostream>
#include <fstream>
#include <list>
#include <set>

　　

回调函数定义：

typedef HRESULT (__stdcall *XCallbackMethodType)(HWND,BSTR,int);

　　

实现代码如下：

STDMETHODIMP CFileTool::SearchFiles(BSTR topDirectoryName, BSTR key, HWND mainWnd,long callbackAddress)
{
	HINSTANCE dllInst=(HINSTANCE)GetModuleHandle(L"xssfj.dll");

	WCHAR finishedMsg[256]={0};
	LoadString(dllInst,IDS_FILE_DELETESPECIFY_SEARCHSUCCESS,finishedMsg,256);
	XCallbackMethodType callbackMsg=(XCallbackMethodType)callbackAddress;
	DWORD attribute=GetFileAttributesW(topDirectoryName);
	if(!(attribute&FILE_ATTRIBUTE_DIRECTORY))
		return E_INVALIDARG;
	if(!callbackMsg)
		return E_INVALIDARG;
	if(StrStrI(topDirectoryName,key))
	{
		callbackMsg(mainWnd,topDirectoryName,2);
		callbackMsg(mainWnd,finishedMsg,0);
		return S_OK;
	}
	std::stack<WCHAR*> directoryNameStack;
	WCHAR* tmpStackData=(WCHAR*)calloc(MAX_PATH,sizeof(WCHAR));
	lstrcpyW(tmpStackData,topDirectoryName);
	directoryNameStack.push(tmpStackData);
	while(!directoryNameStack.empty())
	{
		WCHAR* currentDirName=directoryNameStack.top();
		directoryNameStack.pop();
		callbackMsg(mainWnd,currentDirName,1);
		WCHAR tmpParentPath[MAX_PATH]={0};
		lstrcpy(tmpParentPath,currentDirName);
		if(currentDirName[lstrlen(currentDirName)-1]!='\\')
		{
			lstrcat(tmpParentPath,L"\\");
			lstrcat(currentDirName,L"\\*.*");
		}
		else
			lstrcat(currentDirName,L"*.*");
		WIN32_FIND_DATA meiju={0};

		HANDLE tmpHandle=FindFirstFile(currentDirName,&meiju);
		if(tmpHandle!=INVALID_HANDLE_VALUE&&tmpHandle)
		{
			if(lstrcmpW(meiju.cFileName,L".")!=0&&lstrcmpW(meiju.cFileName,L"..")!=0)
			{
				if(StrStrI(meiju.cFileName,key))
				{
					WCHAR tmpFsObj[MAX_PATH]={0};
					lstrcpyW(tmpFsObj,tmpParentPath);
					lstrcat(tmpFsObj,meiju.cFileName);
					callbackMsg(mainWnd,tmpFsObj,2);
				}
			}
			do
			{
				DWORD tmpFileResult=FindNextFile(tmpHandle,&meiju);
				if(tmpFileResult==ERROR_NO_MORE_FILES||tmpFileResult==0)
					break;
				if(lstrcmpW(meiju.cFileName,L".")==0||lstrcmpW(meiju.cFileName,L"..")==0)
					continue;
				if(StrStrI(meiju.cFileName,key))
				{
					WCHAR tmpFsObj[MAX_PATH]={0};
					lstrcpyW(tmpFsObj,tmpParentPath);
					lstrcat(tmpFsObj,meiju.cFileName);
					callbackMsg(mainWnd,tmpFsObj,2);
				}
				else
				{
					WCHAR tmpFsobjPath[MAX_PATH]={0};
					lstrcpy(tmpFsobjPath,tmpParentPath);
					lstrcat(tmpFsobjPath,meiju.cFileName);
					callbackMsg(mainWnd,tmpFsobjPath,1);
					DWORD tmpFileAttribute=GetFileAttributes(tmpFsobjPath);
					if(tmpFileAttribute&FILE_ATTRIBUTE_DIRECTORY)
					{
						WCHAR* tmpData=(WCHAR*)calloc(MAX_PATH,sizeof(WCHAR));
						lstrcpy(tmpData,tmpFsobjPath);
						directoryNameStack.push(tmpData);
					}
				}
			}
			while(true);
			FindClose(tmpHandle);
		}
		free(currentDirName);
	}
	callbackMsg(mainWnd,finishedMsg,0);
	return S_OK;
}