[杂题]URAL2047. Maths

题意：构造一个长度为n的串，使得 除了第一个以外，每个位置的前缀和的因子个数恰好等于该位置上的数。

n$\le 100000$

举个例子$a_i$：2   4    6     6    4    8    4    8    4   8

前缀和   ：     6   12   18   22  30  34  42  46  54

6的因子：1 2 3 6 为4个  等于a[2]

12的因子：1 2 3 4 6 12 为6个  等于a[3]

18的因子：1 2 3 6 9 18 为6个  等于a[4]

...

...

54的因子：1 2 3 6 9 18 27 54 为8个 等于a[9]

所有都满足，则该列合法

一开始一直在想到哪儿为止会Impossible

然后就打算暴力一发 看到哪儿为止

后来发现正着写，根本写不出来。

于是发现把每个数的因子数写出来，倒着减回去，

每个数回去都只有一条路，最长的就是答案。

比如

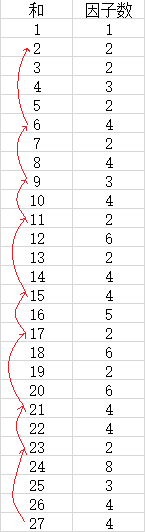
27这个数回去 长度为9

26这个数回去 长度为6

...

每个数回去都有一个长度

后来发现只需知道 “那个数减去因子个数” 的 那个数 回去有多长+1就好啦

那只要预处理一下因子个数

正着for一遍，O(1)就能得到长度

(for的是 和 ， 长度就是题目输入的n ， 需要输出的是 长度最长的那一串回去的路上的数的因子数)

那么打个这样的表，只需1秒钟

int phi[];
int pri()
{
    memset(phi, , sizeof(phi));
    for(int i=;i<=;i++)
        for(int j=i;j<=;j+=i)
            phi[j]++;
}

int dp[];
void pre()
{
    memset(dp, , sizeof(dp));
    dp[]=, dp[]=;
    for(int i=;i<=;i++)
    {
        int num=phi[i]+;
//        if(num>300 || dp[i-num]==-1)
//            dp[i]=-1;
//        else
            dp[i]=dp[i-num]+;
//        printf("%d %d\n", i, dp[i]);
        if(dp[i]>=)
        {
            printf("%d %d\n", i, dp[i]);
            break;
        }
    }
}

int main()
{
//    freopen("out.txt", "w", stdout);
    pri();
    pre();
    return ;
}

得到的这个1568617就是n为100000的最后一个数

要得到n个数，倒着减回去就好了

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 typedef pair<int, int> PI;
 const int N=1e5+;
 const double eps=1e-;
 const int mod=1e9+;

 int ans[], d;
 int phi[];
 void pre()
 {
     memset(phi, , sizeof(phi));
     for(int i=;i<=;i++)
         for(int j=i;j<=;j+=i)
             phi[j]++;
     int x=;
     d=;
     while(x)
     {
         ans[d++]=x;
         int num=phi[x]+;
         x-=num;
     }
 }

 int main()
 {
     pre();
     int n;
     while(~scanf("%d",&n))
     {
         int sum=;
         for(int i=d-, j=;j<=n;j++, i--)
         {
             printf("%d", ans[i]-sum);
             sum=ans[i];
             if(j==n)
                 puts("");
             else
                 putchar(' ');
         }
     }
     return ;
 }

Ural 2047