扩展KMP--求字符串S的所有后缀和字符串T的最长公共前缀

在解上面这个问题前我们要先解决一个类似的问题：求字符串s的所有后缀和s本身的最长公共前缀；

我们用next[]数组保存这些值；

现在我们假设要求next[ x ],并且next[ i ] 0<i<x的值都已经求出;

我们设p = k + next[k] - 1， k是使p最大的 i  (0<i<x);如图:

现在整理一下问题：

　　已知：s[k..p] == s[ 0 .. next[ k ]-1 ],求s[x .. n-1]与s[0 .. n-1]的最长公共前缀；

　　由s[k .. p] == s[ 0 .. next[ k ]-1 ] 得：

s[x .. p] == s[x-k .. next[ k ]-1 ]    ---------1//这个是显然的

并设L1=p-x+1;

因为x-k肯定是小于x的所以  L2=next[x-k]是已知的,得：

s[0 ..  L2-1] == s[x-k .. x-k+L2-1];      --------2

通过等式1,2可以推出 s[0 .. k1] == s[x .. k2]

if  L1<=L2  then  如下图

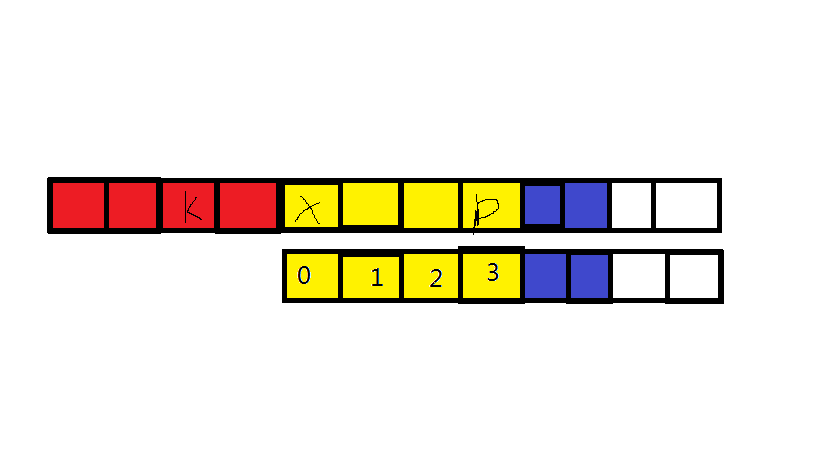
表示s[0 .. L1-1] == s[x .. x+L1-1]但不能确定蓝色部分是否相等，所以需要继续比下去

if  L1 > L2   then 如下图：

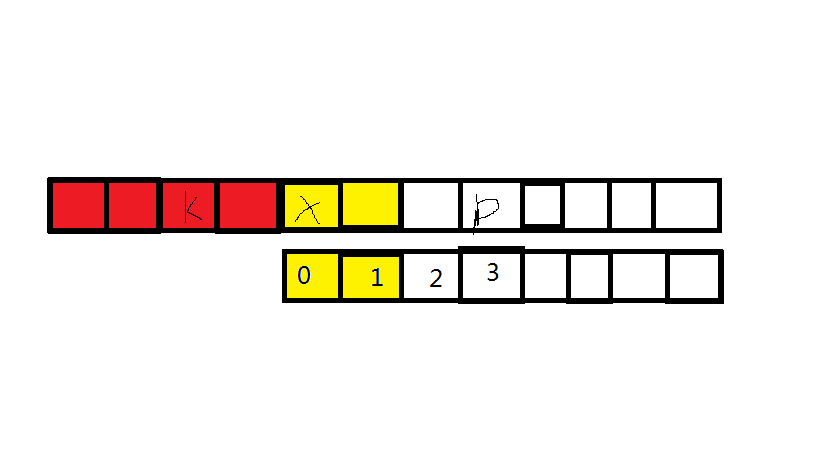
表示s[0 ..  L2-1] == s[x .. x+L2-1] 而且因为L2 = next[x-k]使得s[L2] != s[x+L2]

所以next[x] = L2;

证明：假设s[L2]==s[x+L2]，又因为s[x+L2]==s[x-k+L2]//由1推出

所以s[L2]==s[x-k+L2] 所以next[x-k]==L2+1与next[x-k]==L2矛盾

 void getNext(char *s,int next[]){
     int nn = strlen(s);
     next[] = nn;
     int p = ;
     while (p+ < nn && s[p] == s[p+]) p++;
     next[] = p;
     int k = , L;
     for (int i = ; i < nn; i++){
         p =     k + next[k] - ; L = next[i - k];
         if (i + L <= p) next[i] = L;
         else {
             int j = p - i + ;
             if (j < ) j = ;
             while (i + j < nn && s[i + j] == s[j]) j++;
             next[i] = j; k = i;

         }
     }
 /*    for (int i=0;i<nn;i++){
         cout<< next[i] <<" ";
     }cout<<endl;
 */
 }

回到原来的问题

此时已经求出next[]，我们用extend[]保存字符串S的所有后缀和字符串T的最长公共前缀的值

我们重复上面的过程：

现在我们假设要求extend[ x ],并且extend[ i ] 0<i<x的值都已经求出;

我们设p = k + extend[k] - 1， k是使p最大的 i  (0<i<x);如图：

现在整理一下问题：

　　已知：s[k..p] == T[ 0 .. extend[ k ]-1 ],求s[x .. n-1]与T[0 .. m-1]的最长公共前缀；

　　由s[k .. p] == T[ 0 .. extend[ k ]-1 ] 得：

s[x .. p] == T[x-k .. extend[ k ]-1 ]    ---------1//这个是显然的

并设L1=p-x+1;

因为x-k肯定是小于x的所以  L2=next[x-k]是已知的,得：

T[0 ..  L2-1] == T[x-k .. x-k+L2-1];      --------2

通过等式1,2可以推出 T[0 .. k1] == s[x .. k2]

if  L1<=L2  then  如下图

表示T[0 .. L1-1] == s[x .. x+L1-1]但不能确定蓝色部分是否相等，所以需要继续比下去

if  L1 > L2   then 如下图：

表示T[0 ..  L2-1] == s[x .. x+L2-1] 而且因为L2 = extend[x-k]使得T[L2] != s[x+L2]

所以extend[x] = L2;

证明：假设T[L2]==s[x+L2]，又因为s[x+L2]==T[x-k+L2]//由1推出

所以T[L2]==s[x-k+L2] 所以extend[x-k]==L2+1与extend[x-k]==L2矛盾

 void getExtend(char *s,char *T,int extend[]){
     int nn = strlen(s) ,mm = strlen(T);
     getNext(s,next);
     int p = ;
     while (p < nn && s[p] == T[p]) p++;
     extend[] = p;
     //extend[1] = p;
     int k = , L;
     for (int i = ; i < nn; i++){
         p =     k + extend[k] - ; L = next[i - k];
         if (i + L <= p) extend[i] = L;
         else {
             int j = p - i + ;
             if (j < ) j = ;
             while (i + j < nn && s[i + j] == T[j]) j++;
             extend[i] = j; k = i;

         }
     }
 /*    for (int i=0;i<nn;i++){
         cout<< extend[i] <<" ";
     }cout<<endl;
 */
 }

时间复杂度分析：

对于s串，每一位最多比较一次所以时间是O(n)的；