[转]python起步之卡尔曼滤波

原文地址：http://www.niwozhi.net/demo_c65_i50946.html

关于卡尔曼滤波的理论这里不打算讲了，就是那个5个基本的公式，这里直接给出公式：

公式1：X(k|k-1) = AX(k-1 | k-1) + BU(k) + W(k)

公式2：P(k|k-1) = AP(k-1|k-1)A' + Q(k)

公式3：X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)

公式4：Kg(k) = P(k|k-1)H'/{HP(k|k-1)H' + R} //卡尔曼增益

公式5：P(k|k) = (1- Kg(k) H) P(k|k-1)

另外，Z(k) = HX(k) + V，Z是测量值，X是系统值，W是过程噪声，V是测量噪声，H是测量矩阵，A是转移矩阵，Q是W的协方差，R是V的协方差，X(k|k-1)是估计值；X(k|k)是X(k|k-1)的最优估计值，即滤波估计值；P(k|k-1)是估计值误差方差矩阵，P(k|k)是滤波误差方差矩阵。

下面给出Python版本的卡尔曼滤波小程序，这里设置A=1，H=1，BU=0,W=0：

# -*- coding=utf-8 -*-
# Kalman filter example demo in Python

# A Python implementation of the example given in pages 11-15 of "An
# Introduction to the Kalman Filter" by Greg Welch and Gary Bishop,
# University of North Carolina at Chapel Hill, Department of Computer
# Science, TR 95-041,
# http://www.cs.unc.edu/~welch/kalman/kalmanIntro.html

# by Andrew D. Straw
#coding:utf-8
import numpy
import pylab

#这里是假设A=1，H=1的情况

# intial parameters
n_iter = 50
sz = (n_iter,) # size of array
x = -0.37727 # truth value (typo in example at top of p. 13 calls this z)
z = numpy.random.normal(x,0.1,size=sz) # observations (normal about x, sigma=0.1)

Q = 1e-5 # process variance

# allocate space for arrays
xhat=numpy.zeros(sz)      # a posteri estimate of x
P=numpy.zeros(sz)         # a posteri error estimate
xhatminus=numpy.zeros(sz) # a priori estimate of x
Pminus=numpy.zeros(sz)    # a priori error estimate
K=numpy.zeros(sz)         # gain or blending factor

R = 0.1**2 # estimate of measurement variance, change to see effect

# intial guesses
xhat[0] = 0.0
P[0] = 1.0

for k in range(1,n_iter):
    # time update
    xhatminus[k] = xhat[k-1]  #X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0
    Pminus[k] = P[k-1]+Q      #P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1

    # measurement update
    K[k] = Pminus[k]/( Pminus[k]+R ) #Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1
    xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k]) #X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1
    P[k] = (1-K[k])*Pminus[k] #P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1

pylab.figure()
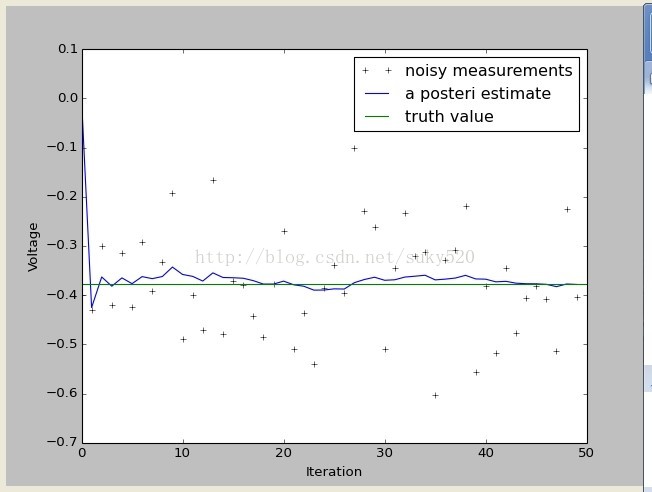
pylab.plot(z,'k+',label='noisy measurements')     #测量值
pylab.plot(xhat,'b-',label='a posteri estimate')  #过滤后的值
pylab.axhline(x,color='g',label='truth value')    #系统值
pylab.legend()
pylab.xlabel('Iteration')
pylab.ylabel('Voltage')

pylab.figure()
valid_iter = range(1,n_iter) # Pminus not valid at step 0
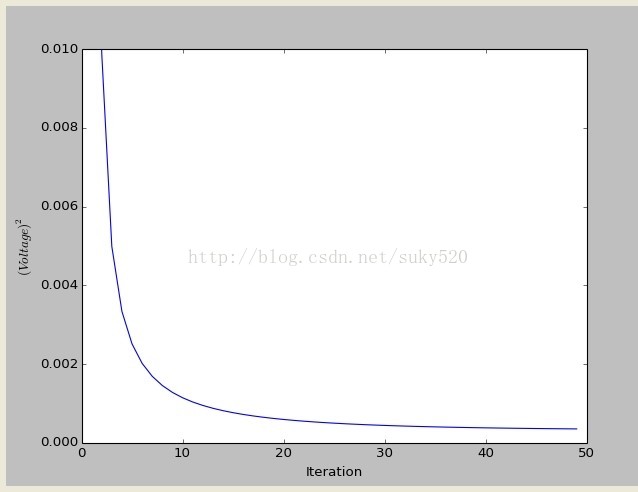
pylab.plot(valid_iter,Pminus[valid_iter],label='a priori error estimate')
pylab.xlabel('Iteration')
pylab.ylabel('$(Voltage)^2$')
pylab.setp(pylab.gca(),'ylim',[0,.01])
pylab.show()

结果：