MATLAB神经网络（6） PID神经元网络解耦控制算法——多变量系统控制

6.1 案例背景

6.1.1 PID神经元网络结构

PID神经元网络从结构上可以分为输入层、隐含层和输出层三层，$n$个控制量的PID神经元网络包含$n$个并列的相同子网络，各个子网络间既相互独立，又通过网络连接权值相互联系。每个子网络的输入层有两个神经元，分别接收控制量的目标值和当前值。每个子网络的隐含层由比例元、积分元和微分元构成，分别对应着PID控制器中的比例控制、积分控制和微分控制。PID神经元网络按被控系统控制量的个数可以分为控制单变量系统的单控制量神经元网络和控制多变量系统的多控制量神经元网络。其中单控制量神经元网络是PID神经元网络的基本形式，多控制量神经元网络可以看成是多个单控制量神经元网络的组合形式。

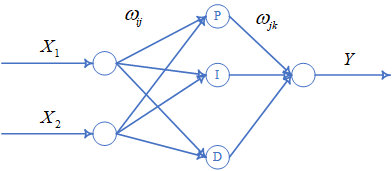
$X_{1}$是控制量的控制目标，$X_{2}$是控制量当前值，$Y$是神经元网络计算得到的控制律，${\omega _{ij}}$和${\omega _{jk}}$是网络权值，从中可以看到单控制量神经元网络是一个三层前向神经元网络，网络结构为2-3-1，隐含层包含比例元、积分元和微分元三个神经元。

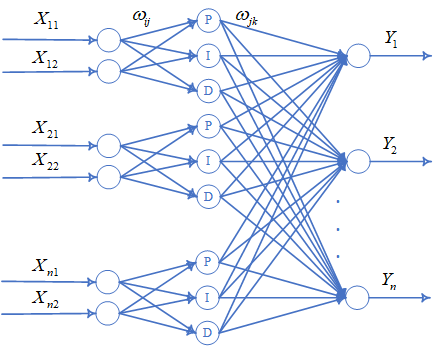
多控制量神经元网络可以看成多个单控制量网络的并联连接，$X_{11},X_{21},...,X_{n1}$是控制量的控制目标，$X_{12},X_{22},...,X_{n2}$是控制量的当前值，$Y_{1},Y_{2},...,Y_{n}$是多控制量神经元网络计算得到的控制律，${\omega _{ij}}$和${\omega _{jk}}$是网络权值。

6.1.2 控制率

• 输入层：输出数据$x_{si}$等于输入数据$X_{si}$：${x_{si}}(k) = {X_{si}}(k)$；
• 隐含层：输入值\[ne{t_{sj}}(k) = \sum\limits_{i = 1}^2 {{\omega _{ij}}{x_{si}}(k)\;\;\;j = 1,2,3} \]比例神经元\[{u_{s1}} = ne{t_{s1}}(k)\]积分神经元\[{u_{s2}} = ne{t_{s2}}(k) + ne{t_{s2}}(k - 1)\]微分神经元\[{u_{s3}} = ne{t_{s3}}(k) - ne{t_{s3}}(k - 1)\]
• 输出层：\[{y_k} = \sum\limits_{s = 1}^n {\sum\limits_{j = 1}^3 {{\omega _{jk}}{u_{sj}}(k)} } \]

6.1.3 权值修正

误差计算公式：\[J = \sum {E = \sum\limits_{k = 1}^n {{{[{y_h}(k) - r(k)]}^2}} } \]其中$n$为输出节点个数，$y_{h}(k)$为预测输出，$r(k)$为控制目标。

• 输出层到隐含层：\[{\omega _{jk}}(k + 1) = {\omega _{jk}}(k) - \eta \frac{{\partial J}}{{\partial {\omega _{jk}}}}\]
• 输入层到输出层：\[{\omega _{ij}}(k + 1) = {\omega _{ij}}(k) - \eta \frac{{\partial J}}{{\partial {\omega _{ij}}}}\]

其中$\eta$为学习速率。

6.1.4 控制对象

传递函数：

\[\left\{ \begin{array}{l}
{y_1}(k) = 0.4{y_1}(k - 1) + {u_1}(k - 1)/[1 + {u_1}{(k - 1)^2}] + 0.2{u_1}{(k - 1)^3} + 0.5{u_2}(k - 1) + 0.3{y_2}(k - 1)\\
{y_2}(k) = 0.2{y_2}(k - 1) + {u_2}(k - 1)/[1 + {u_2}{(k - 1)^2}] + 0.4{u_2}{(k - 1)^3} + 0.2{u_1}(k - 1) + 0.3{y_3}(k - 1)\\
{y_3}(k) = 0.3{y_3}(k - 1) + {u_3}(k - 1)/[1 + {u_3}{(k - 1)^2}] + 0.4{u_3}{(k - 1)^3} + 0.4{u_2}(k - 1) + 0.3{y_1}(k - 1)
\end{array} \right.\]

6.2 模型建立

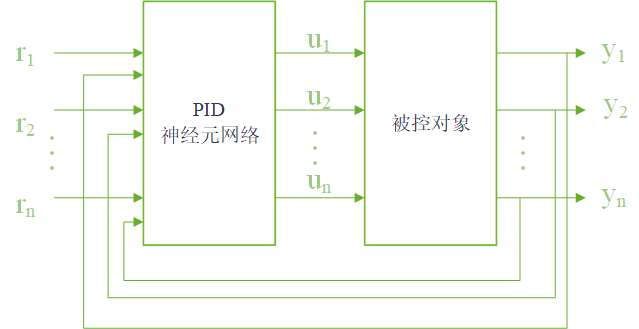
$r_{1}$,r_{2},...,r_{n}$是控制器目标，$u_{1}$,u_{2},...,u_{n}$为控制器规律，$y_{1}$,y_{2},...,y_{n}$为控制器当前值。

3个控制量——3个单神经元网络。

控制量初始值[0,0,0]，控制目标为[0.7,0.4,0.6]，控制时间间隔0.001s。

6.3 编程实现

6.3.1 初始化

%% 基于PID神经网络的系统控制算法
%% 清空环境变量
clc
clear

%% 网络结构初始化
rate1=0.006;rate2=0.001; %学习率
K=3;
y_1=zeros(3,1);y_2=y_1;    %输出值
u_1=zeros(3,1);u_2=u_1;    %控制率
h1i=zeros(3,1);h1i_1=h1i;  %第一个控制量
h2i=zeros(3,1);h2i_1=h2i;  %第二个控制量
h3i=zeros(3,1);h3i_1=h3i;  %第三个控制量
x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;   %隐含层输入

%权值初始化
k0=0.03;

%第一层权值
w11=k0*rand(3,2);
w12=k0*rand(3,2);
w13=k0*rand(3,2);
%第二层权值
w21=k0*rand(1,9);
w22=k0*rand(1,9);
w23=k0*rand(1,9);

%值限定
ynmax=1;ynmin=-1;  %系统输出值限定
xpmax=1;xpmin=-1;  %P节点输出限定
qimax=1;qimin=-1;  %I节点输出限定
qdmax=1;qdmin=-1;  %D节点输出限定
uhmax=1;uhmin=-1;  %输出结果限定

6.3.2 优化

%% 网络迭代优化
for k=1:1:300

    %% 控制量输出计算
    %--------------------------------网络前向计算--------------------------

    %系统输出
    y1(k)=(0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2);
    y2(k)=(0.2*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.4*u_1(2)^3+0.2*u_1(1))+0.3*y_1(3);
    y3(k)=(0.3*y_1(3)+u_1(3)/(1+u_1(3)^2)+0.4*u_1(3)^3+0.4*u_1(2))+0.3*y_1(1);

    r1(k)=0.7;r2(k)=0.4;r3(k)=0.6;  %控制目标

    %系统输出限制
    yn=[y1(k),y2(k),y3(k)];
    yn(yn>ynmax)=ynmax;
    yn(yn<ynmin)=ynmin;

    %输入层输出
    x1o=[r1(k);yn(1)];x2o=[r2(k);yn(2)];x3o=[r3(k);yn(3)];

    %隐含层
    x1i=w11*x1o;
    x2i=w12*x2o;
    x3i=w13*x3o;

    %比例神经元P计算
    xp=[x1i(1),x2i(1),x3i(1)];
    xp(xp>xpmax)=xpmax;
    xp(xp<xpmin)=xpmin;
    qp=xp;
    h1i(1)=qp(1);h2i(1)=qp(2);h3i(1)=qp(3);

    %积分神经元I计算
    xi=[x1i(2),x2i(2),x3i(2)];
    qi_1=[h1i(2),h2i(2),h3i(2)];
    qi=qi_1+xi;
    qi(qi>qimax)=qimax;
    qi(qi<qimin)=qimin;
    h1i(2)=qi(1);h2i(2)=qi(2);h3i(2)=qi(3);

    %微分神经元D计算
    xd=[x1i(3),x2i(3),x3i(3)];
    xd_1=[x1i_1(3),x2i_1(3),x3i_1(3)];
    qd=xd-xd_1;
    qd(qd>qdmax)=qdmax;
    qd(qd<qdmin)=qdmin;
    h1i(3)=qd(1);h2i(3)=qd(2);h3i(3)=qd(3);

    %输出层计算
    wo=[w21;w22;w23];
    qo=[h1i',h2i',h3i'];qo=qo';
    uh=wo*qo;
    uh(uh>uhmax)=uhmax;
    uh(uh<uhmin)=uhmin;
    u1(k)=uh(1);u2(k)=uh(2);u3(k)=uh(3);  %控制律

    %% 网络权值修正
    %---------------------网络反馈修正----------------------

    %计算误差
    error=[r1(k)-y1(k);r2(k)-y2(k);r3(k)-y3(k)];
    error1(k)=error(1);error2(k)=error(2);error3(k)=error(3);
    J(k)=(error(1)^2+error(2)^2+error(3)^2);   %调整大小
    ypc=[y1(k)-y_1(1);y2(k)-y_1(2);y3(k)-y_1(3)];
    uhc=[u_1(1)-u_2(1);u_1(2)-u_2(2);u_1(3)-u_2(3)];

    %隐含层和输出层权值调整

    %调整w21
    Sig1=sign(ypc./(uhc(1)+0.00001));
    dw21=sum(error.*Sig1)*qo';
    w21=w21+rate2*dw21;

    %调整w22
    Sig2=sign(ypc./(uh(2)+0.00001));
    dw22=sum(error.*Sig2)*qo';
    w22=w22+rate2*dw22;

    %调整w23
    Sig3=sign(ypc./(uh(3)+0.00001));
    dw23=sum(error.*Sig3)*qo';
    w23=w23+rate2*dw23;

    %输入层和隐含层权值调整
    delta2=zeros(3,3);
    wshi=[w21;w22;w23];
    %调整w11
    for t=1:1:3
        delta2(1:3,t)=error(1:3).*sign(ypc(1:3)./(uhc(t)+0.00000001));
    end
    for j=1:1:3
        sgn(j)=sign((h1i(j)-h1i_1(j))/(x1i(j)-x1i_1(j)+0.00001));
    end

    s1=sgn'*[r1(k),y1(k)];
    wshi2_1=wshi(1:3,1:3);
    alter=zeros(3,1);
    dws1=zeros(3,2);
    for j=1:1:3
        for p=1:1:3
            alter(j)=alter(j)+delta2(p,:)*wshi2_1(:,j);
        end
    end

    for p=1:1:3
        dws1(p,:)=alter(p)*s1(p,:);
    end
    w11=w11+rate1*dws1;

    %调整w12
    for j=1:1:3
        sgn(j)=sign((h2i(j)-h2i_1(j))/(x2i(j)-x2i_1(j)+0.0000001));
    end
    s2=sgn'*[r2(k),y2(k)];
    wshi2_2=wshi(:,4:6);
    alter2=zeros(3,1);
    dws2=zeros(3,2);
    for j=1:1:3
        for p=1:1:3
            alter2(j)=alter2(j)+delta2(p,:)*wshi2_2(:,j);
        end
    end
    for p=1:1:3
        dws2(p,:)=alter2(p)*s2(p,:);
    end
    w12=w12+rate1*dws2;

    %调整w13
    for j=1:1:3
        sgn(j)=sign((h3i(j)-h3i_1(j))/(x3i(j)-x3i_1(j)+0.0000001));
    end
    s3=sgn'*[r3(k),y3(k)];
    wshi2_3=wshi(:,7:9);
    alter3=zeros(3,1);
    dws3=zeros(3,2);
    for j=1:1:3
        for p=1:1:3
            alter3(j)=(alter3(j)+delta2(p,:)*wshi2_3(:,j));
        end
    end
    for p=1:1:3
        dws3(p,:)=alter2(p)*s3(p,:);
    end
    w13=w13+rate1*dws3;

    %参数更新
    u_2=u_1;u_1=uh;
    y_2=y_1;y_1=yn;
    h1i_1=h1i;h2i_1=h2i;h3i_1=h3i;
    x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;
end

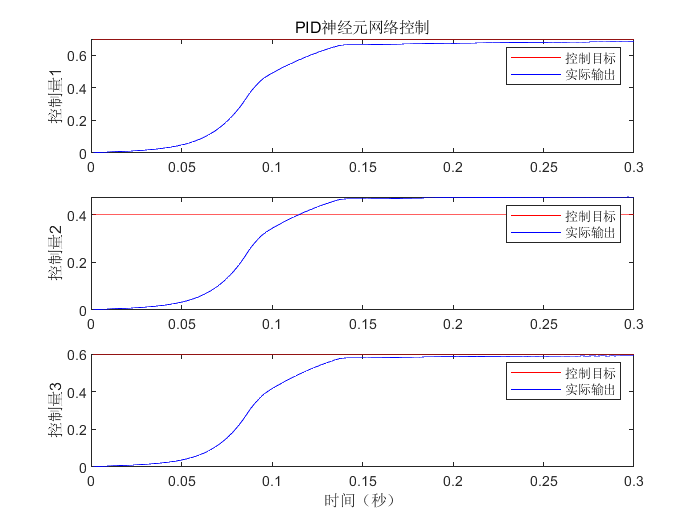
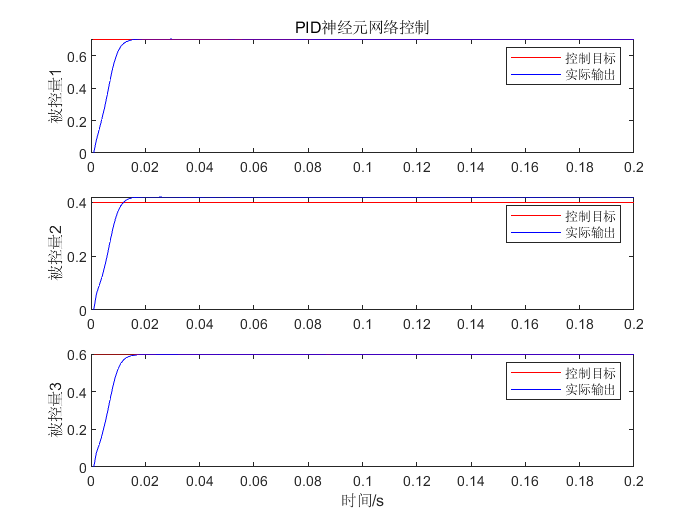
6.3.3 结果分析

%% 结果分析
time=0.001*(1:k);
figure(1)
subplot(3,1,1)
plot(time,r1,'r-',time,y1,'b-');
title('PID神经元网络控制','fontsize',12);
ylabel('控制量1','fontsize',12);
legend('控制目标','实际输出');

subplot(3,1,2)
plot(time,r2,'r-',time,y2,'b-');

ylabel('控制量2','fontsize',12);
legend('控制目标','实际输出');
subplot(3,1,3)
plot(time,r3,'r-',time,y3,'b-');
xlabel('时间（秒）','fontsize',12);ylabel('控制量3','fontsize',12);
legend('控制目标','实际输出');

figure(2)
plot(time,u1,'r-',time,u2,'g-',time,u3,'b');
title('PID神经网络提供给对象的控制输入');
xlabel('时间'),ylabel('被控量');
legend('u1','u2','u3');grid

figure(3)
figure(3)
plot(time,J,'r-');
axis([0,0.2,0,1]);grid
title('控制误差曲线','fontsize',12);
xlabel('时间','fontsize',12);ylabel('控制误差','fontsize',12);

6.3.4 Simulink仿真

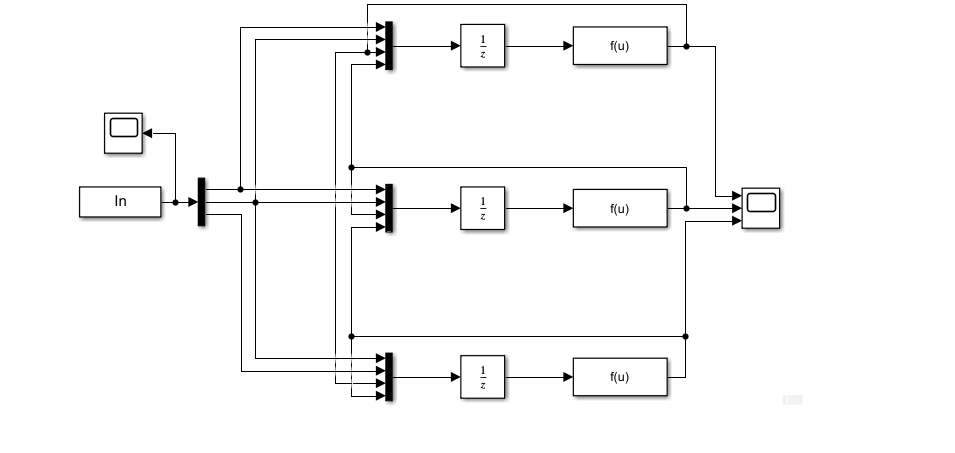
6.4 扩展

6.4.1 增加动量项

\[\begin{array}{l}
{\omega _{jk}}(k + 1) = {\omega _{jk}}(k) - \eta \frac{{\partial J}}{{\partial {\omega _{jk}}}} + {\eta _1}[{\omega _{jk}}(k) - {\omega _{jk}}(k - 1)]\\
{\omega _{ij}}(k + 1) = {\omega _{ij}}(k) - \eta \frac{{\partial J}}{{\partial {\omega _{ij}}}} + {\eta _1}[{\omega _{ij}}(k) - {\omega _{ij}}(k - 1)]
\end{array}\]

6.4.2 神经元系数

\[\begin{array}{l}
{u_{s1}} = {k_p} \cdot ne{t_{s1}}(k)\\
{u_{s2}} = {k_i} \cdot [ne{t_{s2}}(k) + ne{t_{s2}}(k - 1)]\\
{u_{s3}} = {k_d} \cdot [ne{t_{s3}}(k) - ne{t_{s3}}(k - 1)]
\end{array}\]

6.4.3 PID神经元网络权值优化

粒子群/遗传算法——解决可能陷入局部最优的问题，改善控制效果。