POJ 2287 田忌赛马

Tian Ji -- The Horse Racing

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 17699		Accepted: 5461

Description

Here is a famous story in Chinese history.

That was about 2300 years ago. General Tian Ji was a
high official in the country Qi. He likes to play horse racing with the
king and others.

Both of Tian and the king have three horses in different classes,
namely, regular, plus, and super. The rule is to have three rounds in a
match; each of the horses must be used in one round. The winner of a
single round takes two hundred silver dollars from the loser.

Being the most powerful man in the country, the king has so nice
horses that in each class his horse is better than Tian's. As a result,
each time the king takes six hundred silver dollars from Tian.

Tian Ji was not happy about that, until he met Sun Bin, one of the
most famous generals in Chinese history. Using a little trick due to
Sun, Tian Ji brought home two hundred silver dollars and such a grace in
the next match.

It was a rather simple trick. Using his regular class horse race
against the super class from the king, they will certainly lose that
round. But then his plus beat the king's regular, and his super beat the
king's plus. What a simple trick. And how do you think of Tian Ji, the
high ranked official in China?

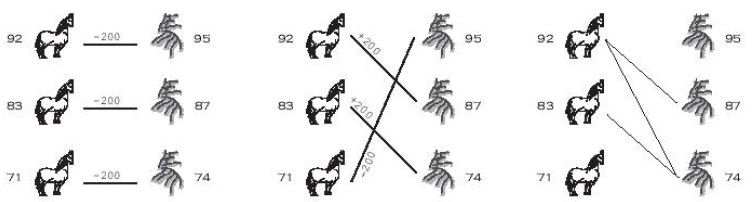
Were Tian Ji lives in nowadays, he will certainly laugh at himself.
Even more, were he sitting in the ACM contest right now, he may discover
that the horse racing problem can be simply viewed as finding the
maximum matching in a bipartite graph. Draw Tian's horses on one side,
and the king's horses on the other. Whenever one of Tian's horses can
beat one from the king, we draw an edge between them, meaning we wish to
establish this pair. Then, the problem of winning as many rounds as
possible is just to find the maximum matching in this graph. If there
are ties, the problem becomes more complicated, he needs to assign
weights 0, 1, or -1 to all the possible edges, and find a maximum
weighted perfect matching...

However, the horse racing problem is a very special case of
bipartite matching. The graph is decided by the speed of the horses -- a
vertex of higher speed always beat a vertex of lower speed. In this
case, the weighted bipartite matching algorithm is a too advanced tool
to deal with the problem.

In this problem, you are asked to write a program to solve this special case of matching problem.

Input

The
input consists of up to 50 test cases. Each case starts with a positive
integer n ( n<=1000) on the first line, which is the number of
horses on each side. The next n integers on the second line are the
speeds of Tian's horses. Then the next n integers on the third line are
the speeds of the king's horses. The input ends with a line that has a
single `0' after the last test case.

Output

For each input case, output a line containing a single number, which is the maximum money Tian Ji will get, in silver dollars.

Sample Input

3
92 83 71
95 87 74
2
20 20
20 20
2
20 19
22 18
0

Sample Output

200
0
0

/*
贪心策略：
1，如果田忌的最快马快于齐王的最快马，则两者比。
（因为若是田忌的别的马很可能就赢不了了，所以两者比）
2，如果田忌的最快马慢于齐王的最快马，则用田忌的最慢马和齐王的最快马比。
（由于所有的马都赢不了齐王的最快马，所以用损失最小的，拿最慢的和他比）
3，若相等，则比较田忌的最慢马和齐王的最慢马
3.1，若田忌最慢马快于齐王最慢马，两者比。
（田忌的最慢马既然能赢一个就赢呗，而且齐王的最慢马肯定也得有个和他比，所以选最小的比他快得。）
3.2，其他，则拿田忌的最慢马和齐王的最快马比。
（反正所有的马都比田忌的最慢马快了，所以这匹马必输，选贡献最大的，干掉齐王的最快马）
*/

#include<iostream>
#include<algorithm>
#include<string.h>
#include<string>
#include<vector>
#include<stack>
#include<math.h>
#define mod 998244353
#define ll long long
#define MAX 0x3f3f3f3f
using namespace std;
int a[],b[];
int n;
bool cmp(int x,int y)
{
    return x>y;
}
int main()
{
    while(scanf("%d",&n)&&n)
    {
        for(int i=;i<n;i++)
            scanf("%d",&a[i]);
        for(int i=;i<n;i++)
            scanf("%d",&b[i]);
        sort(a,a+n,cmp);
        sort(b,b+n,cmp);
        int mx_a=,mn_a=n-,mx_b=,mn_b=n-,ans=;
        while(n--)
        {
            if(a[mx_a]>b[mx_b])//田忌最快的马比齐王最快的马快
            {
                ans=ans+;
                mx_a++;
                mx_b++;
            }
            else if(a[mx_a]<b[mx_b])//田忌最快的马比齐王最快的马慢
            {
                ans=ans-;
                mn_a--;
                mx_b++;
            }
            else//快马速度相等，比较慢马
            {
                if(a[mn_a]>b[mn_b])//田忌最慢的马比齐王最慢的马快
                {
                    ans=ans+;
                    mn_a--;
                    mn_b--;
                }
                else if(a[mn_a]<b[mx_b])//必输，用田忌慢马消耗齐王快马
                {
                    ans=ans-;
                    mn_a--;
                    mx_b++;
                }
                else//相等,还是用田忌慢马消耗快马
                {
                    //ans=ans-200;
                    mn_a--;
                    mx_b++;
                }
            }
        }
        printf("%d\n",ans);
    }
}