LSTM的备胎，用卷积处理时间序列——TCN与因果卷积（理论+Python实践）

什么是TCN

TCN全称Temporal Convolutional Network，时序卷积网络，是在2018年提出的一个卷积模型，但是可以用来处理时间序列。

卷积如何处理时间序列

时间序列预测，最容易想到的就是那个马尔可夫模型：

\[P(y_k|x_k,x_{k-1},...,x_1)
\]

就是计算某一个时刻的输出值，已知条件就是这个时刻之前的所有特征值。上面公式中，P表示概率，可以不用管这个，\(y_k\)表示k时刻的输出值（标签），\(x_k\)表示k时刻的特征值。

如果使用LSTM或者是GRU这样的RNN模型，自然是可以处理这样的时间序列模型的，毕竟RNN生来就是为了这个的。

但是这个时间序列模型，宏观上思考的话，其实就是对这个这个时刻之前的数据做某个操作，然后生成一个标签，回想一下在卷积在图像中的操作，其实有异曲同工。（这里不理解也无妨，因为我之前搞了一段时间图像处理，所以对卷积相对熟悉一点）。

一维卷积

假设有一个时间序列，总共有五个时间点，比方说股市，有一个股票的价格波动：[10,13,12,14,15]:

TCN中，或者说因果卷积中，使用的卷积核大小都是2，我也不知道为啥不用更大的卷积核，看论文中好像没有说明这个，如果有小伙伴知道原因或者有猜想，可以下方评论处一起讨论讨论。

卷积核是2，那么可想而知，对上面5个数据做一个卷积核为2的卷积是什么样子的：

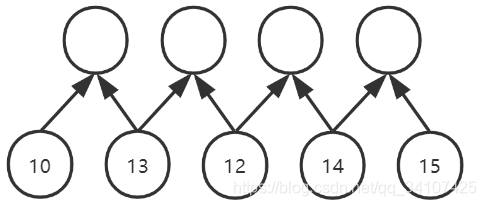
五个数据经过一次卷积，可以变成四个数据，但是每一个卷积后的数据都是基于两个原始数据得到的，所以说，目前卷积的视野域是2。

可以看到是输入是5个数据，但是经过卷积，变成4个数据了，在图像中有一个概念是通过padding来保证卷积前后特征图尺寸不变，所以在时间序列中，依然使用padding来保证尺寸不变：

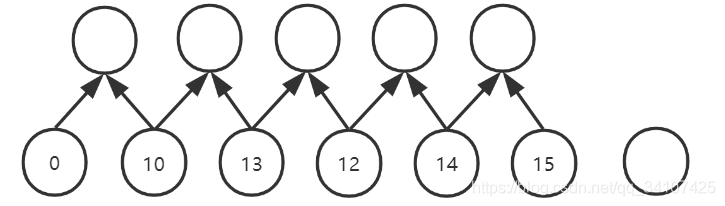
padding是左右两头都增加0，如果padding是1的话，就是上图的效果，其实会产生6个新数据，但是秉着：“输入输出尺寸相同”和“我们不能知道未来的数据”，所以最后边那个未来的padding，就省略掉了，之后再代码中会体现出来。

总之，现在我们大概能理解，对时间序列卷积的大致流程了，也就是对一维数据卷积的过程（图像卷积算是二维）。

下面看如何使用Pytorch来实现一维卷积：

net = nn.Conv1d(in_channels=1,out_channels=1,kernel_size=2,stride=1,padding=1,dilation=1)

其中的参数跟二维卷积非常类似，也是有通道的概念的。这个好好品一下，一维数据的通道跟图像的通道一样，是根据不同的卷积核从相同的输入中抽取出来不同的特征。kernel_size=2之前也说过了，padding=1也没问题，不过这个公式中假如输入5个数据+padding=1，会得到6个数据，最后一个数据被舍弃掉。dilation是膨胀系数，下面的下面会讲。

因果卷积

因果卷积是在wavenet这个网络中提出的，之后被用在了TCN中。

TCN的论文链接：
因果卷积应为就是：Causal Convolutions。

之前已经讲了一维卷积的过程了，那么因果卷积，其实就是一维卷积的一种应用吧算是。

假设想用上面讲到的概念，做一个股票的预测决策模型，然后希望决策模型可以考虑到这个时间点之前的4个时间点的股票价格进行决策，总共有3种决策：

0：不操作，1：买入，2：卖出

所以其实就是一个分类问题。因为要求视野域是4，所以按照上面的设想，要堆积3个卷积核为2的1维卷积层：

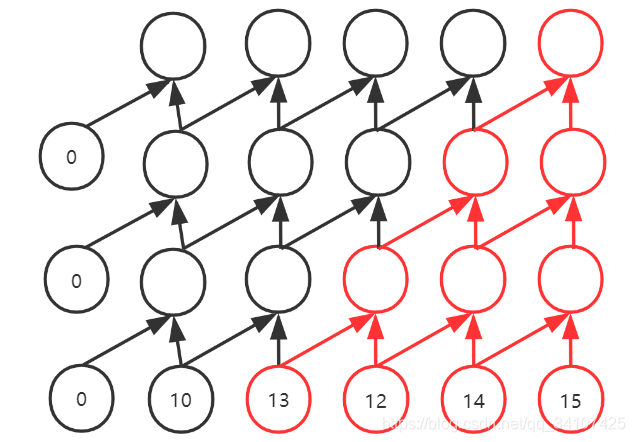
三次卷积，可以让最后的输出，拥有4个视野域。就像是上图中红色的部分，就是做出一个决策的过程。

股票数据，往往是按照分钟记录的，那少说也是十万、百万的数据量，我们决策，想要考虑之前1000个时间点呢？视野域要是1000，那意味着要999层卷积？啥计算机吃得消这样的计算。所以引入了膨胀因果卷积。

膨胀因果卷积

英文是Dilated Causal Convolution。这个其实就是空洞卷积啦，不确定在之前的博文中有没有讲过这个概念（最近别人要求在写一个非常长的教程，和博客中的博文可能会有记忆混乱的情况2333）
反正就是，这个空洞卷积、或者叫扩张卷积、或者叫膨胀卷积就是操作dilation这个参数。

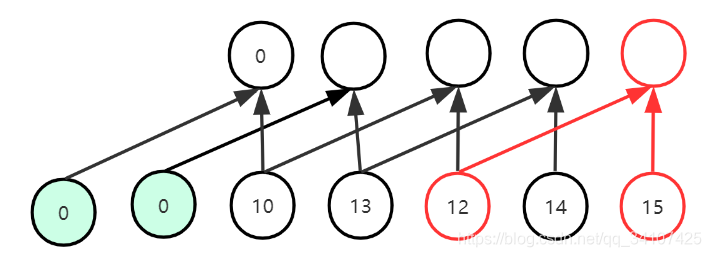
如图，这个就是dilation=2的时候的情况，与之前的区别有两个：
看红色区域：可以看到卷积核大小依然是2，但是卷积核之间变得空洞了，隔过去了一个数据；如果dilation=3的话，那么可以想而知，这个卷积核中间会空的更大，会隔过去两个数据。
看淡绿色数据：因为dilation变大了，所以相应的padding的数量从1变成了2，所以为了保证输入输出的特征维度相同，padding的数值等于dalition的数值（在卷积核是2的情况下，严格说说：padding=（kernel_size-1）*dilation）

然后我们依然实现上面那个例子，每次决策想要视野域为4：

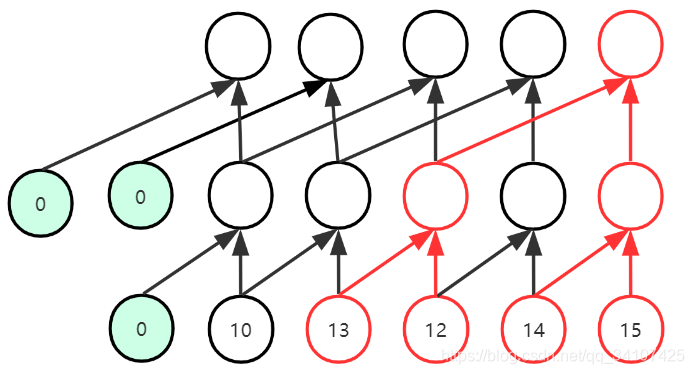
可以看到，第一次卷积使用dilation=1的卷积，然后第二次使用dilation=2的卷积，这样通过两次卷积就可以实现视野域是4.

那么假设事业域要是8呢？那就再加一个dilation=4的卷积。dilation的值是2的次方，然后视野域也是2的次方的增长，那么就算是要1000视野域，那十层大概就行了。

这里有一个动图，挺好看的：

TCN结构

TCN基本就是一个膨胀因果卷积的过程，只是上面我们实现因果卷积就只有一个卷积层。而TCN的稍微复杂一点（但是不难！）

卷积结束后会因为padding导致卷积之后的新数据的尺寸B>输入数据的尺寸A，所以只保留输出数据中前面A个数据；
卷积之后加上个ReLU和Dropout层，不过分吧这要求。
然后TCN中并不是每一次卷积都会扩大一倍的dilation，而是每两次扩大一倍的dilation
总之TCN中的基本组件：TemporalBlock()是两个dilation相同的卷积层，卷积+修改数据尺寸+relu+dropout+卷积+修改数据尺寸+relu+dropout
之后弄一个Resnet残差连接来避免梯度消失，结束！

关于Resnet的内容:【从零学习PyTorch】如何残差网络resnet作为pre-model +代码讲解+残差网络resnet是个啥其实不看也行，不妨碍理解TCN

模型的PyTorch实现（最好了解一点PyTorch）

如果不了解的话，emm，我要安利我的博文了2333：

从零学习pytorch 第5课 PyTorch模型搭建三要素

# 导入库

import torch

import torch.nn as nn

from torch.nn.utils import weight_norm

# 这个函数是用来修剪卷积之后的数据的尺寸，让其与输入数据尺寸相同。

class Chomp1d(nn.Module):

    def __init__(self, chomp_size):

        super(Chomp1d, self).__init__()

        self.chomp_size = chomp_size

    def forward(self, x):

        return x[:, :, :-self.chomp_size].contiguous()

可以看出来，这个函数就是第一个数据到倒数第chomp_size的数据，这个chomp_size就是padding的值。比方说输入数据是5，padding是1，那么会产生6个数据没错吧，那么就是保留前5个数字。

# 这个就是TCN的基本模块，包含8个部分，两个（卷积+修剪+relu+dropout）

# 里面提到的downsample就是下采样，其实就是实现残差链接的部分。不理解的可以无视这个

class TemporalBlock(nn.Module):

    def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):

        super(TemporalBlock, self).__init__()

        self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,

                                           stride=stride, padding=padding, dilation=dilation))

        self.chomp1 = Chomp1d(padding)

        self.relu1 = nn.ReLU()

        self.dropout1 = nn.Dropout(dropout)

        self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,

                                           stride=stride, padding=padding, dilation=dilation))

        self.chomp2 = Chomp1d(padding)

        self.relu2 = nn.ReLU()

        self.dropout2 = nn.Dropout(dropout)

        self.net = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,

                                 self.conv2, self.chomp2, self.relu2, self.dropout2)

        self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None

        self.relu = nn.ReLU()

        self.init_weights()

    def init_weights(self):

        self.conv1.weight.data.normal_(0, 0.01)

        self.conv2.weight.data.normal_(0, 0.01)

        if self.downsample is not None:

            self.downsample.weight.data.normal_(0, 0.01)

    def forward(self, x):

        out = self.net(x)

        res = x if self.downsample is None else self.downsample(x)

        return self.relu(out + res)

最后就是TCN的主网络了：

class TemporalConvNet(nn.Module):

    def __init__(self, num_inputs, num_channels, kernel_size=2, dropout=0.2):

        super(TemporalConvNet, self).__init__()

        layers = []

        num_levels = len(num_channels)

        for i in range(num_levels):

            dilation_size = 2 ** i

            in_channels = num_inputs if i == 0 else num_channels[i-1]

            out_channels = num_channels[i]

            layers += [TemporalBlock(in_channels, out_channels, kernel_size, stride=1, dilation=dilation_size,

                                     padding=(kernel_size-1) * dilation_size, dropout=dropout)]

        self.network = nn.Sequential(*layers)

    def forward(self, x):

        return self.network(x)

咋用的呢？就是num_inputs就是输入数据的通道数，一般就是1； num_channels应该是个列表，其他的np.array也行，比方说是[2,1]。那么整个TCN模型包含两个TemporalBlock，整个模型共有4个卷积层，第一个TemporalBlock的两个卷积层的膨胀系数\(dilation=2^0=1\)，第二个TemporalBlock的两个卷积层的膨胀系数是\(dilation=2^1=2\).

没了，整个TCN挺简单的，如果之前学过PyTorch和图像处理的一些内容，然后用TCN来上手时间序列，效果会和LGM差不多。（根据最近做的一个比赛），没有跟Wavenet比较过，Wavenet的pytorch资源看起来怪复杂的，因为wavenet是用来处理音频生成的，会更加复杂一点。

总之TCN就这么多，谢谢大家。