Properties in Algebra

附录-Properties in Algebra

部分证明转载自标注，仅作个人整理查阅用。

范数 (norm) \(^{[1]}\)

要更好的理解范数，就要从函数、几何与矩阵的角度去理解，我尽量讲的通俗一些。我们都知道，函数与几何图形往往是有对应的关系，这个很好想象，特别是在三维以下的空间内，函数是几何图像的数学概括，而几何图像是函数的高度形象化，比如一个函数对应几何空间上若干点组成的图形。但当函数与几何超出三维空间时，就难以获得较好的想象，于是就有了映射的概念，映射表达的就是一个集合通过某种关系转为另外一个集合。通常数学书是先说映射，然后再讨论函数，这是因为函数是映射的一个特例。
为了更好的在数学上表达这种映射关系，（这里特指线性关系）于是就引进了矩阵。这里的矩阵就是表征上述空间映射的线性关系。而通过向量来表示上述映射中所说的这个集合，而我们通常所说的基，就是这个集合的最一般关系。于是，我们可以这样理解，一个集合（向量），通过一种映射关系（矩阵），得到另外一个集合（另外一个向量）。
那么向量的范数，就是表示这个原有集合的大小；而矩阵的范数，就是表示这个变化过程的大小的一个度量。那么说到具体几几范数，其不过是定义不同，一个矩阵范数往往由一个向量范数引出，我们称之为算子范数，其物理意义都如我上述所述。

具体怎么用，看不同的领域，看你来自计算机领域 用的比较多的就是迭代过程中收敛性质的判断，如果理解上述的意义，在计算机领域，一般迭代前后步骤的差值的范数表示其大小，常用的是二范数，差值越小表示越逼近实际值，可以认为达到要求的精度，收敛。

L-p范数定义

\[
L_p=\Vert x\Vert_p=\sqrt[p]{\sum_{i=1}^{n}x_i^p}，x=(x_1,\dots,x_n)
\]

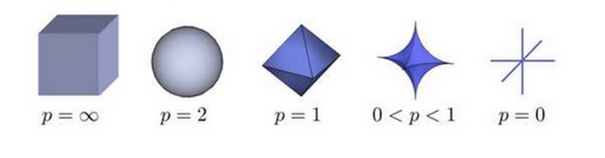
上图表示了p从无穷到0变化时，三维空间中到原点的距离（范数）为1的点构成的图形的变化情况。以常见的L-2范数（p=2）为例，此时的范数也即欧氏距离，空间中到原点的欧氏距离为1的点构成了一个球面。

\(L_0\)范数

\[
L_0=\Vert x\Vert_0=\sqrt[0]{\sum_{i=1}^{n}x_i^0}::=\#\{i|x_i\neq0\}
\]

在实际应用中，由于\(L_0\)范数本身不容易有一个好的数学表示形式，给出上面问题的形式化表示是一个很难的问题，故被人认为是一个NP难问题。所以在实际情况中，\(L_0\)的最优问题会被放宽到\(L_1\)或\(L_2\)下的最优化。 在通常情况下，大家都用"0范数"表示向量\(x\)中非零元素的个数。

\(L_1\)范数

表示向量\(x\)中非零元素的绝对值之和。
\[
L_1=\Vert x\Vert_1=\sqrt[1]{\sum_{i=1}^{n}x_i^1}::=\sum_{i=1}^{n}|x_i|
\]
\(L_1\)范数有很多的名字，例如我们熟悉的曼哈顿距离、最小绝对误差等。使用\(L_1\)范数可以度量两个向量间的差异，如绝对误差和（Sum of Absolute Difference）.

\(L_2\)范数

我们用的最多的度量距离：欧氏距离就是一种\(L_2\)范数，它的定义如下：
\[
L_2=\Vert x\Vert_2=\sqrt[2]{\sum_{i=1}^{n}x_i^2}
\]

\(L_\infty\)范数

主要用来表示向量元素中的最大项值，通常用此来表示：
\[
L_\infty=\Vert x\Vert_\infty=::=max\{|x_i|\}
\]

实对称矩阵

对称矩阵（Symmetric Matrices）：是指以主对角线为对称轴，各元素对应相等的矩阵。在线性代数中，对称矩阵是一个方形矩阵，其转置矩阵和自身相等。
\[
A=A^T
\]
实对称矩阵：如果有n阶矩阵A，其矩阵的元素都为实数，且矩阵A的转置等于其本身（\(a_{ij}=a_{ji}\)），则称A为实对称矩阵。

实对称矩阵里的元素全是实数，而对称矩阵只说明\(A=A^T\)，没说明矩阵中的元素是实数， 阵中的元素不仅可以是实数，也可以是虚数，甚至元素本身就是一个矩阵或其它更一般的数学对象，实对称矩阵就说明了矩阵中的元素要是实数。

• 性质1：实对称矩阵的特征值都是实数

$$

$$

• 性质2：实对称属于不同特征值的特征向量正交

$$

$$

• 性质3：若\(\lambda_0\)是实对称矩阵A的 k 重特征值，则与对\(\lambda_0\)应的有 k 个线性无关的特征向量

$$

$$

• 性质4：n 阶实对称矩阵 正交相似 于以特征值为对角的对角矩阵。

$$

$$

矩阵的逆

若方阵\(A\)满足\(|A|\neq0\)，则称\(A\)为非退化方阵或非奇异方阵，反正，则称其为退化方阵，下令\(A=(a_{ij})\)为一非退化方阵，令：
\[
B'=\frac{(A_{ij})}{|A|}
\]
则有\(AB=BA=I\)，称\(B\)为\(A\)的逆，记作\(B=A^{-1}\)，易证\(B\)也是一个非退化方阵，且\(A\)的逆是唯一的。

• \(AA^{-1}=A^{-1}A=I\)
• \((A')^{-1}=(A^{-1})'\)
• 若\(A,C\)均为\(p\)阶非退化方阵，则：\((AC)^{-1}=C^{-1}A^{-1}\)
• \(|A|^{-1}=|A^{-1}|\)
• 若\(A\)为正交矩阵，则\(A^{-1}=A'\)
• 若\(A=diag(a_{ii})\)非退化，则：\(A^{-1}=diag(a_{ii}^{-1})\)
• 若\(A,B\)为非退化方阵，则

\[
\left(
\begin{array}{cc}
A&O\\
O&B
\end{array}
\right)^{-1}=
\left(
\begin{array}{cc}
A^{-1}&O\\
O&B^{-1}
\end{array}
\right)
\]

非奇异矩阵的分块矩阵求逆

设\(A\)是\(p\)阶满秩矩阵，它的逆矩阵为\(A^{-1}\),他们可表示为下列分块矩阵：
\[
A=\left(
\begin{array}{c|c}
A_{11}&A_{12}\\\hline
A_{21}&A_{22}
\end{array}
\right)，
A^{-1}=\left(
\begin{array}{c|c}
A^{11}&A^{12}\\\hline
A^{21}&A^{22}
\end{array}
\right)
\]
其中\(A_{11},A^{11}\)均为\(r\times r\)矩阵，\(A_{22},A^{22}\)均为\(s\times s\)矩阵，且\(r+s=p\)。

\(^{[1]}\)范数对于数学的意义？1范数、2范数、无穷范数