初识DP动态规划

一、多阶段决策过程的最优化问题

在现实生活中,有类活 动的过程，由于 它的特殊性，可将过程分成若干个互相阶段。在它的每一阶段都需要作出决策,从而使整个过程达到最好的活动效果。当阶段决策的选取不是任意确定的，它依赖于当前面临的状态,又影响以后的发展，当段决策确定后，就组成一个决策序列,因而也就确定了整个过程的一条活动路线,这个问题看作是个前后关联具有链状结构的 多阶段过程就称为多阶段决策过程，这就称为多阶段决策问题。

多阶段决策过程,是指这样的一类特殊的活动过程,问题可以按时间顺序分解互联系的阶段，在每-个阶段都要作出决策,全部过程的决策是-个决策序列。

二、能采用动态规划求解的问题的一般要具有3个性质：

最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只 与当前状态有关。

有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）

三、动态规划基本概念

状态：描述事物的性质，不同事物有不同的性质，因而用不同的状态来刻画。对问题的求解状态的描述是分阶段的。

决策：根据题意要求，对每个阶段所做出的某种选择性操作。

状态转移方程：用数学公式描述与阶段相关的状态间的演变规律。

四、解题步骤：

1. 拆分问题
2. 定义状态(并找出初状态)
3. 状态转移方程

五、模型方法

第一种递归搜索法。

第二种递归搜索法+记忆。

第三种递推式法。

六、例题

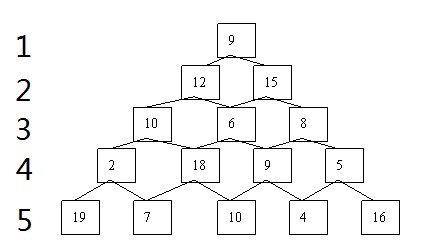
数塔问题



思路分析：

贪心不可解，每一步都会影响后续的操作。

在用动态规划考虑数塔问题时可以自顶向下的分析，自底向上的计算。

从顶点出发时到底向左走还是向右走应取决于是从左走能取到最大值还是从右走能取到最大值，只要左右两道路径上的最大值求出来了才能作出决策。同样的道理下一层的走向又要取决于再下一层上的最大值是否已经求出才能决策。这样一层一层推下去，直到倒数第二层时就非常明了。

所以第一步对第五层的8个数据，做如下四次决策：

如果经过第四层2，则在第五层的19和7中肯定是19；

如果经过第四层18，则在第五层的7和10中肯定是10；

如果经过第四层9，则在第五层的10和4中肯定是10；

如果经过第四层5，则在第五层的4和16中肯定是16；

经过一次决策，问题降了一阶。5层数塔问题转换成4层数塔问题，如此循环决策…… 最后得到1阶的数塔问题。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100+10;
int num[MAXN][MAXN];
int dp[MAXN][MAXN];
int main()
{
    int t;
    scanf("%d", &t);
    while( t-- )
    {
        memset(dp, 0, sizeof(dp));
        int n;
        scanf("%d", &n);
        for( int i=1; i<=n; i++ )
        {
            for( int j=1; j<=i; j++ )
                scanf("%d", &num[i][j]);
        }
        for( int j=1; j<=n; j++ )
            dp[n][j] = num[n][j];
        for( int i = n-1; i >= 1; i-- )
        {
             for( int j=1; j <= i; j++ )
             {
                 dp[i][j] = num[i][j] + max(dp[i+1][j], dp[i+1][j+1]);
             }
        }
        printf("%d\n", dp[1][1] );
    }
    return 0;
}