Codeforces 1290B/1291D - Irreducible Anagrams

题目大意：

两串字符串 s 和 t 是否 anagrams（下文简称ANA） 的定义是：

　　是否能将 s 内的字母打乱顺序后再拼接得到 t

我们考虑互相ANA的两串字符串 s 和 t

我们称 t 是 s 的 reducible anagram（下文简称RANA），在当存在一个数 k≥2，且满足下面的定义时：

　　1、s 可以被分割成 k 个非空子串 s1,s2,...,sk

　　2、t 对应着 s 的每个子串的长度也这样分割 t1,t2,...tk

　　3、分割后对应的 si 和 ti （1≤i≤k）都是互相ANA的

如果不存在，那么则称 t 是 s 的 irreducible anagram （下文简称IRANA）

给定一个字符串 S

q 次询问，每次询问 S 中 l 到 r 位置这一段子串 s

问这段子串 s 是否存在至少一个IRANA

是，输出Yes，否，输出No

解题思路：

问这段子串 s 是否存在至少一个IRANA

那么，只要找到一种 t 不是 s 的RANA即可

先直接给出结论：

　　1、只有单个字符

　　2、首尾字符不同

　　3、包含三种及以上的字符

分成以下五种情况（带上了证明，写得很繁琐）：

　　1、根据RANA的定义1可以得知，如果给定的字符串长度为1，无法找到k>=2使其分成至少两个非空子串，所以这个字符串本身就是自己的IRANA，输出Yes

　　2、如果给定的字符串只有一种字符，那么 t 只有一种情况，不论怎么分 t 都是 s 的RANA，不存在IRANA，输出No

　　3、排除了只存在一种字符的情况，接下来如果给定的字符串首尾是不同的，以a和b举例，可得

　　

　　此时会出现四种组合，但我们只考虑交换首尾顺序的那个 t 即可，即

　　

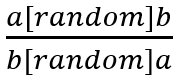
　　只考虑a和b，不妨看上a下b为1，看上b下a为-1，其余为0，可得从首位置加到末位置最后会得出0（化成坐标系能看到首尾处在同一条水平线上），故得到上述例子的折线图为

　　

　　因为只要接触这条水平线，就说明可以以这个点为分割线分成左右两块

　　但总能找出一种组合使得这条折线不触碰初始的水平线到达终点（即如果有其他的1和-1的组合，把1排在-1前面即可）

　　所以至少存在一种 t 是 s 的IRANA，输出Yes

　　4、如果给定的字符串这个字符串首尾是相同的，且只包含两种字符，拿a和b举例

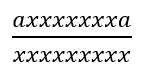　　上为s，下为t，其中x代表a或者b任意字符

　　假设刚开始t相等于s，再对t任意字符进行交换操作

　　因为相同的两个字符交换没有意义，只考虑不同字符交换

　　会出现4种情况：

　　　　1、上a下a与上b下a形式，下面两个进行交换，变成上a下a和上b下a（不变）

　　　　2、上a下a与上b下b形式，下面两个进行交换，变成上a下b和上b下a

　　　　3、上a下b与上b下a形式，下面两个进行交换，变成上a下a和上b下b

　　　　4、上a下b与上b下b形式，下面两个进行交换，变成上a下b和上b下b（不变）

　　可以得到，有多少组上a下b形式的，就会有多少组上b下a的形式与其对应

　　又因为s首尾字符相同，不妨先让这两字符为a

　　此时，首尾只存在上a下a和上a下b两种形式

　　　　1、如果上a下a存在一组，直接单独拎出来分成一块，即如下图分成两块

　　　　

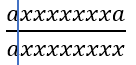
　　　　此时的 t 是 s 的RANA

　　　　2、如果上a下a都不存在，即首尾都是上a下b形式，那么中间必定存在两组及以上（偶数组）的上b下a形式

　　　　

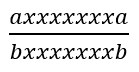
　　　　同上述方式做折线图得

　　

　　　　可知，左侧第二点和右侧倒数第二点中间一定是连续的，所以必定会接触水平线大于等于1次

　　　　而每次接触这条水平线，就说明可以以这个点为分割线分成左右两块

　　　　即 t 肯定是 s 的RANA

　　　　综上，不存在IRANA，输出No

　　5、如果给定的字符串这个字符串首尾是相同的，且包含三种及以上字符

　　将首尾的这种字符全部取出来排在中间，再选择第一个剩余的按顺序来的第一个字符排在其后，剩余的随机排在其左侧

　　例如

　　

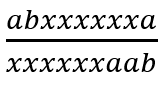
　　此时 t 串的a会排在b前，且最前面会出现上a下x的形式

　　要想让第一个位置开始，即上a下x开始能有相同的前缀种类及数量（先去尝试寻找是否存在ANA的一段子串，即必须让一段前缀能够独自分块），就必须要找到一个上x下a形式与其“相消”

　　那么就可以直接看到上x下a的位置，加入第一个上x下a形式就能与受位置上a下x“相消”，即

　　

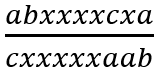
　　但是到这个位置过，其中还有一个上b下x的位置需要消除

　　消除需要寻找上x下b这种情况，但是在 t 串中b排在了a后的位置

　　但是，在 t 串中的位置到b之前，t 串中的a已经全部搜索完，而 s 串中的最后一定会有至少一个a

　　很明显，这样的前缀种类及数量永远不可能相等

　　可以得出这样排列的 t 是 s 的IRANA，输出Yes

至此，5种情况全部找完了，代码实现很简单，做一个字母前缀和就行了

#include<bits/stdc++.h>
using namespace std;
struct type{
    int v[];
}ar[];
string s;
int l,r;
bool solve(){
    if(l==r||s[l]!=s[r])
        return true;
    l--;
    int i,kind=;
    for(i=;i<;i++)
        if(ar[r].v[i]-ar[l].v[i])
            kind++;
    if(kind>=)
        return true;
    return false;
}
int main(){
    ios::sync_with_stdio();
    cin.tie();cout.tie();
    int q,i,len;
    cin>>s>>q;
    len=s.size();
    s=" "+s;
    for(i=;i<=len;i++){
        ar[i]=ar[i-];
        ar[i].v[s[i]-'a']++;
    }
    while(q--){
        cin>>l>>r;
        cout<<(solve()?"Yes":"No")<<'\n';
    }

    return ;
}