LeetCode-Stack-Easy

简单题

1. 有效的括号（leetcode-20）

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。 

有效字符串需满足：
1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 注意空字符串可被认为是有效字符串。 

示例 1:       输入: "()"          输出: true
示例 2:       输入: "()[]{}"      输出: true
示例 3:       输入: "(]"          输出: false
示例 4:       输入: "([)]"        输出: false
示例 5:       输入: "{[]}"        输出: true 

Related Topics 栈 字符串

1) 栈

遍历输入字符串

1. 当前字符是左括号时，入栈；

2. 当前字符是右括号时，观察栈顶元素

   • 栈顶元素为与当前右括号匹配的左括号，弹出左括号，继续遍历字符串（说明两者相匹配）。
   • 栈顶元素不是当前右括号匹配的左括号，返回false（括号不匹配）。

使用栈+Hashmap实现

import java.util.HashMap;
import java.util.Stack;

class Solution {
public boolean isValid(String s) {
    if(s.length()%2==1){
        return false;
    }

    HashMap<Character, Character> map = new HashMap<>();
    map.put(')', '(');
    map.put(']', '[');
    map.put('}', '{');

    Stack<Character> stack = new Stack<>();

    for(int i=0; i<s.length(); i++){
        char ch = s.charAt(i);
        if(ch == '(' || ch == '[' || ch == '{'){
            stack.push(ch);
        }else if(!stack.empty() && stack.peek() == map.get(ch)){
            stack.pop();
        }else{
            return false;
        }
    }

    return stack.empty();

}

}

也可以不使用Hashmap

栈实现

public boolean isValid(String s) {
        if(s.isEmpty())
            return true;
        Stack stack=new Stack();
        for(char c:s.toCharArray()){
            if(c=='(')
                stack.push(')');
            else if(c=='{')
                stack.push('}');
            else if(c=='[')
                stack.push(']');
            else if(stack.empty()||c!=stack.pop())
                return false;
        }
        return stack.empty();
    }

2）字符串替换

不推荐 复杂度高，仅作为了解。时间复杂度是O(n平方)。

展示代码

public boolean isValid(String s) {
        if (s.contains("()") || s.contains("[]") || s.contains("{}")) {
            return isValid(s.replace("()", "").replace("[]", "").replace("{}", ""));
        } else {
            return "".equals(s);
        }
    }

2. 最小栈（leetcode-155）

设计一个支持 push ，pop ，top 操作，并能在【常数时间】内检索到最小元素的栈。
1. push(x) —— 将元素 x 推入栈中。
2. pop() —— 删除栈顶的元素。
3. top() —— 获取栈顶元素。
4. getMin() —— 检索栈中的最小元素。 

示例:
输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

提示： pop、top 和 getMin 操作总是在 非空栈 上调用。 

Related Topics 栈 设计

1）辅助栈 MinStack存储最小值

思路一

对于栈来说，如果一个元素 a 在入栈时，栈里有其它的元素 b, c, d，那么无论这个栈在之后经历了什么操作，只要 a 在栈中，b, c, d 就一定在栈中，因为在 a 被弹出之前，b, c, d 不会被弹出。

因此，在操作过程中的任意一个时刻，只要栈顶的元素是 a，那么就可以确定栈里面现在的元素一定是 a, b, c, d。

那么，在每个元素 a 入栈时把当前栈的最小值 m 存储起来。在这之后无论何时，如果栈顶元素是 a，就可以直接返回存储的最小值 m。

基于上述思路：

只需要设计一个数据结构，使得每个元素 a 与其相应的最小值 m 时刻保持一一对应。因此可以使用一个辅助栈，与元素栈同步插入与删除，用于存储与每个元素对应的最小值。

1. 当一个元素要入栈时，取当前辅助栈的栈顶存储的最小值，与当前元素比较得出最小值，将这个最小值插入辅助栈中；

2. 当一个元素要出栈时，把辅助栈的栈顶元素也一并弹出；

3. 在任意一个时刻，栈内元素的最小值就存储在辅助栈的栈顶元素中。

辅助栈 MinStack存储最小值

import java.util.Stack;

class MinStack {
private <Integer> s;
private <Integer> minStack;

/** initialize your data structure here. */
public MinStack() {
    s = new Stack<>();
    minStack = new Stack<>();
}

public void push(int x) {
    s.push(x);
    if(s.isEmpty()){
        minStack.push(x);
    }else{
        minStack.push(Math.min(x, minStack.peek()));
    }
}

public void pop() {
    if(!s.isEmpty()){
        s.pop();
        minStack.pop();
    }
}

public int top() {
    if(!s.isEmpty()){
        return s.peek();
    }else{
        throw new RuntimeException("stack is empty");
    }
}

public int getMin() {
    if(!s.isEmpty()){
        return minStack.peek();
    }else{
        throw new RuntimeException("stack is empty");
    }
}

}

思路二

1. 将第一个元素入栈。

2. 新加入的元素如果【大于】栈顶元素，那么新加入的元素就【不处理】。

3. 新加入的元素如果【小于等于】栈顶元素，那么就将新元素【入栈】。

4. 出栈元素【不等于】栈顶元素，【不操作】。

5. 出栈元素【等于】栈顶元素，那么就将栈顶元素【出栈】。

辅助栈思路二

class MinStack {
/** initialize your data structure here. */
private Stack<Integer> stack;
private Stack<Integer> minStack;

public MinStack() {
    stack = new Stack<>();
    minStack = new Stack<>();
}

public void push(int x) {
    stack.push(x);
    if (!minStack.isEmpty()) {
        int top = minStack.peek();
        //小于的时候才入栈
        if (x <= top) {
            minStack.push(x);
        }
    }else{
        minStack.push(x);
    }
}

public void pop() {
    int pop = stack.pop();

    int top = minStack.peek();
    //等于的时候再出栈
    if (pop == top) {
        minStack.pop();
    }

}

public int top() {
    return stack.peek();
}

public int getMin() {
    return minStack.peek();
}

}

2）单向链表(增加一个min值域)

用一个链表即可实现栈的基本功能，在 Node 节点中增加一个 min 字段，每次加入一个节点时，只要同时确定它的 min 值即可。

单向链表实现最小栈

class MinStack {
class Node{

    int value;
    int min;
    Node next;

    Node(int v, int min){
        this.value = v;
        this.min = min;
        next = null;
    }
}

Node head;
/** initialize your data structure here. */
public MinStack() {
    head = new Node(-1,-1);
}

public void push(int x) {
    if(head.next == null){
        head.next = new Node(x, x);
    }else{
        // 头插：每次像链表头插入数据
        Node t = new Node(x, Math.min(x, head.next.min));
        t.next = head.next;
        head.next = t;
    }
}

public void pop() {
    if(head.next != null){
        head.next = head.next.next;
    }else{
        throw new RuntimeException("stack is empty");
    }
}

public int top() {
    if(head.next != null){
        return head.next.value;
    }else{
        throw new RuntimeException("stack is empty");
    }
}

public int getMin() {
    if(head.next != null){
        return head.next.min;
    }else{
        throw new RuntimeException("stack is empty");
    }
}

}

3）一个栈同时存储元素与最小值

• push操作，更新最小值时，同时将之前的最小值入栈。

• pop操作，当删除的元素为最小值时，一次弹出两个元素，第二次弹出的元素为新的最小值

入栈 3
|   |   min = 3
|   |
|_3_|
stack   

入栈 5
|   |   min = 3
| 5 |
|_3_|
stack  

入栈 2 ，同时将之前的 min 值 3 入栈，再把 2 入栈，同时更新 min = 2
| 2 |   min = 2
| 3 |
| 5 |
|_3_|
stack  

入栈 6
| 6 |  min = 2
| 2 |
| 3 |
| 5 |
|_3_|
stack  

出栈 6
| 2 |   min = 2
| 3 |
| 5 |
|_3_|
stack  

出栈 2
| 2 |   min = 2
| 3 |
| 5 |
|_3_|
stack  

出栈 2
|   |  min = 3
| 5 |
|_3_|
stack

一个栈同时存储元素与最小值

class MinStack {
int min = Integer.MAX_VALUE;
Stack<Integer> stack = new Stack<Integer>();
public void push(int x) {
    //当前值更小
    if(x <= min){   //等于的时候要push，连续多个相等，就push多个。因为出栈的时候，会pop多个。
        //将之前的最小值保存
        stack.push(min);
        //更新最小值
        min=x;
    }
    stack.push(x);
}

public void pop() {
    //如果弹出的值是最小值，那么将下一个元素更新为最小值
    if(stack.pop() == min) {
        min=stack.pop();
    }
}

public int top() {
    return stack.peek();
}

public int getMin() {
    return min;
}

}

4）一个栈存储元素差值

1. 每次存入的是原来值 - 当前最小值。

2. 当原来值大于等于当前最小值的时候，存入的肯定就是非负数，所以出栈的时候就是栈中的值 + 当前最小值。

3. 当原来值小于当前最小值的时候，存入的肯定就是负值，此时的值不入栈，用 min 保存起来，同时将差值入栈。

4. 当后续如果出栈元素是负数的时候，那么要出栈的元素其实就是 min。此外之前的 min 值，可以通过栈顶的值和当前 min 值进行还原，就是用 min 减去栈顶元素即可。

入栈 3，存入 3 - 3 = 0
|   |   min = 3
|   |
|_0_|
stack   

入栈 5，存入 5 - 3 = 2
|   |   min = 3
| 2 |
|_0_|
stack  

入栈 2，因为出现了更小的数，所以我们会存入一个负数，这里很关键
也就是存入  2 - 3 = -1, 并且更新 min = 2
对于之前的 min 值 3, 我们只需要用更新后的 min - 栈顶元素 -1 就可以得到
| -1|   min = 2
| 5 |
|_3_|
stack  

入栈 6，存入  6 - 2 = 4
| 4 |   min = 2
| -1|
| 5 |
|_3_|
stack  

出栈，返回的值就是栈顶元素 4 加上 min，就是 6
|   |   min = 2
| -1|
| 5 |
|_3_|
stack  

出栈，此时栈顶元素是负数，说明之前对 min 值进行了更新。
入栈元素 - min = 栈顶元素，入栈元素其实就是当前的 min 值 2
所以更新前的 min 就等于入栈元素 2 - 栈顶元素(-1) = 3
|   | min = 3
| 5 |
|_3_|
stack     

一个栈存储元素差值

public class MinStack {
  long min;
  Stack<Long> stack;

  public MinStack(){
        stack=new Stack<>();
  }

  public void push(int x) {
        if (stack.isEmpty()) {
              min = x;
              stack.push(x - min);
        } else {
              stack.push(x - min);
              if (x < min){
                    min = x; // 更新最小值
              }
        }
  }

  public void pop() {
        if(stack.isEmpty())
              return;

        long pop = stack.pop();
        //弹出的是负值，要更新 min
        if (pop < 0) {
            min = min - pop;
        }
  }

  public int top() {
        long top = stack.peek();
        //负数的话，出栈的值保存在 min 中
        if (top < 0) {
              return (int) (min);
        //出栈元素加上最小值即可
        } else {
              return (int) (top + min);
        }
  }

  public int getMin() {
        return (int) min;
  }

}

3. 用队列实现栈（leetcode-225）

使用队列实现栈的下列操作：
1. push(x) -- 元素 x 入栈
2. pop() -- 移除栈顶元素
3. top() -- 获取栈顶元素
4. empty() -- 返回栈是否为空 

注意:
你只能使用队列的基本操作, 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
你所使用的语言也许不支持队列。 你可以使用 list 或者 deque（双端队列）来模拟一个队列, 只要是标准的队列操作即可。
你可以假设所有操作都是有效的（例如, 对一个空的栈不会调用 pop 或者 top 操作）。 

Related Topics 栈 设计

用队列实现栈

用 queue 去保存数据

1. push 操作正常的加到队列；

2. pop 操作，因为队列是先进先出，栈是先进后出，所以此时应该将队列最后一个元素出队列。只需要将队列中除去最后一个元素，其他元素全部出队列，剩下的最后一个就是要弹出的。然后把之前出了队列的元素再保存起来即可。

用队列实现栈

import java.util.LinkedList;
import java.util.Queue;

//leetcode submit region begin(Prohibit modification and deletion)

class MyStack {
Queue<Integer> queue;
/** Initialize your data structure here. */
public MyStack() {
    queue = new LinkedList<>();
}

/** Push element x onto stack. */
public void push(int x) {
    //add()和remove()方法在失败的时候会抛出异常(不推荐)
    queue.offer(x);
}

/** Removes the element on top of the stack and returns that element. */
public int pop() {
    int qSize = queue.size();
    while(qSize > 1){
        queue.offer(queue.poll());
        qSize--;
    }

    return queue.poll();
}

/** Get the top element. */
public int top() {
    int qSize = queue.size();
    while(qSize > 1){
        queue.offer(queue.poll());
        qSize--;
    }
    int res = queue.poll();
    queue.offer(res);
    return res;
}

/** Returns whether the stack is empty. */
public boolean empty() {
    return queue.isEmpty();
}

}

队列是一种特殊的线性表，它只允许在表的前端进行删除操作，而在表的后端进行插入操作。

Java中，LinkedList类实现了Queue接口，因此可以把LinkedList当成Queue来用。

Queue<Integer> queue = new LinkedList<Integer>();

错误用法

Queue<Integer> q1 = new Queue<Integer>();

会报错：error: Queue is abstract; cannot be instantiated

4. 用栈实现队列（leetcode-232）

使用栈实现队列的下列操作：
1. push(x) -- 将一个元素放入队列的尾部。
2. pop() -- 从队列首部移除元素。
3. peek() -- 返回队列首部的元素。
4. empty() -- 返回队列是否为空。 

示例:
MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek();  // 返回 1
queue.pop();   // 返回 1
queue.empty(); // 返回 false 

说明:
你只能使用标准的栈操作 -- 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。
假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）。 

Related Topics 栈 设计

1）使用两个栈（推荐）

使用两个栈，一个栈输入，一个栈输出。（每个元素只会遍历一次）

• 当需要查看或者出队的时候，若输出栈为空，就将输入栈元素依次放入到输出栈中；若输出栈不为空，直接出栈即可。输出栈的输出顺序和队列是相符的。

• 入栈时，直接入输入栈即可。

使用两个栈实现队列

class MyQueue {
Stack<Integer> input;
Stack<Integer> output;

/** Initialize your data structure here. */
public MyQueue() {
    input = new Stack<>();
    output = new Stack<>();
}

/** Push element x to the back of queue. */
public void push(int x) {
    input.push(x);
}

/** Removes the element from in front of queue and returns that element. */
public int pop() {
    if(!output.isEmpty()){
        return output.pop();
    }

    while(!input.isEmpty()){
        output.push(input.pop());
    }

    return output.pop();
}

/** Get the front element. */
public int peek() {
    if(!output.isEmpty()){
        return output.peek();
    }

    while(!input.isEmpty()){
        output.push(input.pop());
    }

    return output.peek();
}

/** Returns whether the queue is empty. */
public boolean empty() {
    return input.isEmpty() && output.isEmpty();
}

}

2）使用临时栈

通过一个临时栈，每次 pop 的时候将原来的元素都保存到临时栈中，只剩下最后一个元素，这个元素是第一个加入栈中的，对于队列就是第一个应该弹出的。然后再把原来的元素还原到栈中即可。

（每个元素会遍历两遍）

使用临时栈

class MyQueue {
Stack<Integer> s1;

/** Initialize your data structure here. */
public MyQueue() {
    s1 = new Stack<>();
}

/** Push element x to the back of queue. */
public void push(int x) {
    s1.push(x);
}

/** Removes the element from in front of queue and returns that element. */
public int pop() {
    Stack<Integer> s2 = new Stack<>();
    while(s1.size()>1){
        s2.push(s1.pop());
    }
    int res = s1.pop();
    while(!s2.isEmpty()){
        s1.push(s2.pop());
    }
    return res;
}

/** Get the front element. */
public int peek() {
    Stack<Integer> s2 = new Stack<>();
    while(s1.size()>1){
        s2.push(s1.pop());
    }
    int res = s1.pop();
    s1.push(res);
    while(!s2.isEmpty()){
        s1.push(s2.pop());
    }
    return res;
}

/** Returns whether the queue is empty. */
public boolean empty() {
    return s1.isEmpty();
}

}

5. 下一个更大元素 I（leetcode-496）

给定两个 没有重复元素 的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出 -1 。 

示例 1:
      输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
      输出: [-1,3,-1]

解释:
- 对于num1中的数字4，你无法在第二个数组中找到下一个更大的数字，因此输出 -1。
- 对于num1中的数字1，第二个数组中数字1右边的下一个较大数字是 3。
- 对于num1中的数字2，第二个数组中没有下一个更大的数字，因此输出 -1。 

示例 2:
      输入: nums1 = [2,4], nums2 = [1,2,3,4].
      输出: [3,-1]

解释:
- 对于 num1 中的数字 2 ，第二个数组中的下一个较大数字是 3 。
- 对于 num1 中的数字 4 ，第二个数组中没有下一个更大的数字，因此输出 -1 。

提示：
- nums1和nums2中所有元素是唯一的。
- nums1和nums2 的数组大小都不超过1000。 

Related Topics 栈

单调栈+HashMap

思路：可以忽略数组 nums1，先对将 nums2 中的每一个元素，求出其下一个更大的元素。随后对于将这些答案放入哈希映射（HashMap）中，再遍历数组 nums1，并直接找出答案。对于 nums2，可以使用单调栈来解决这个问题。

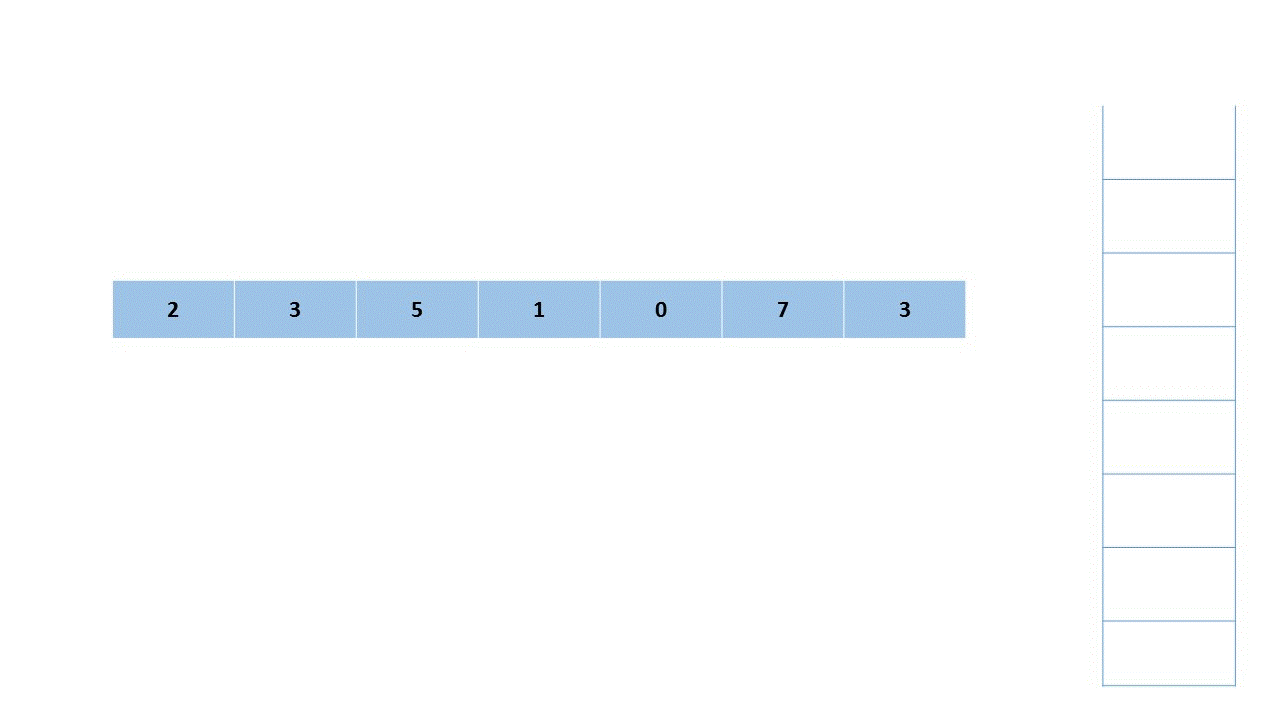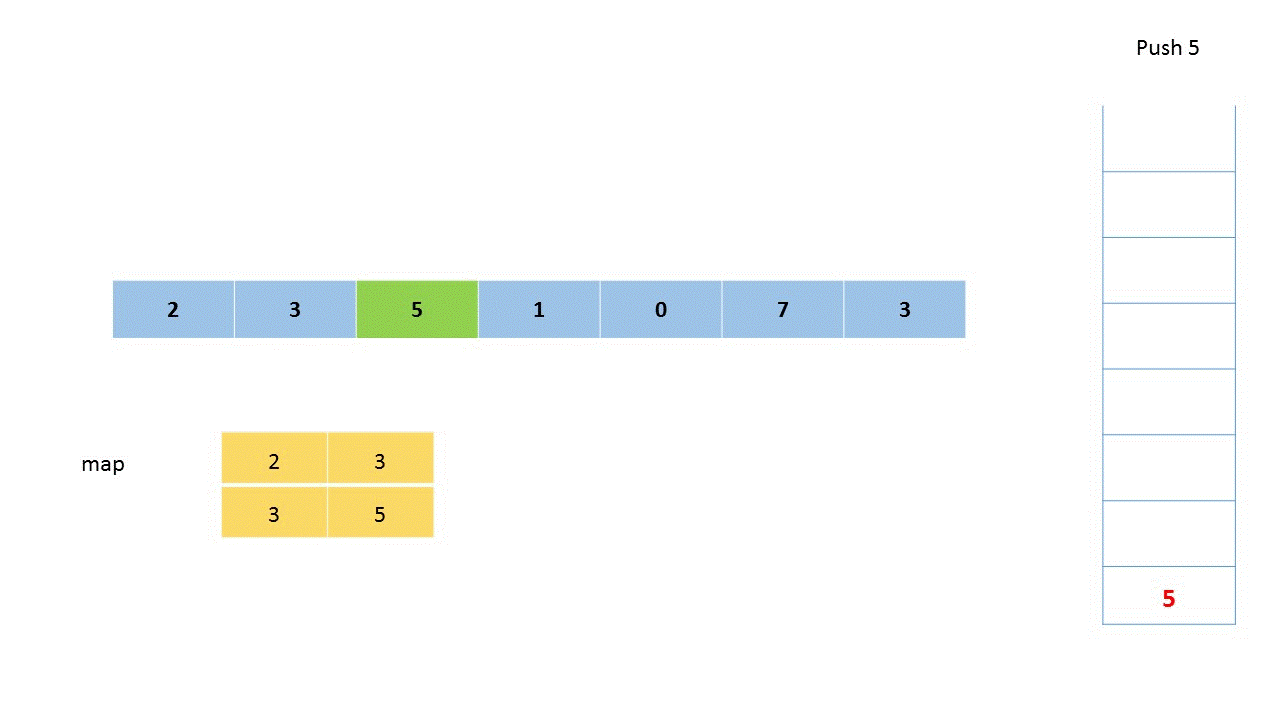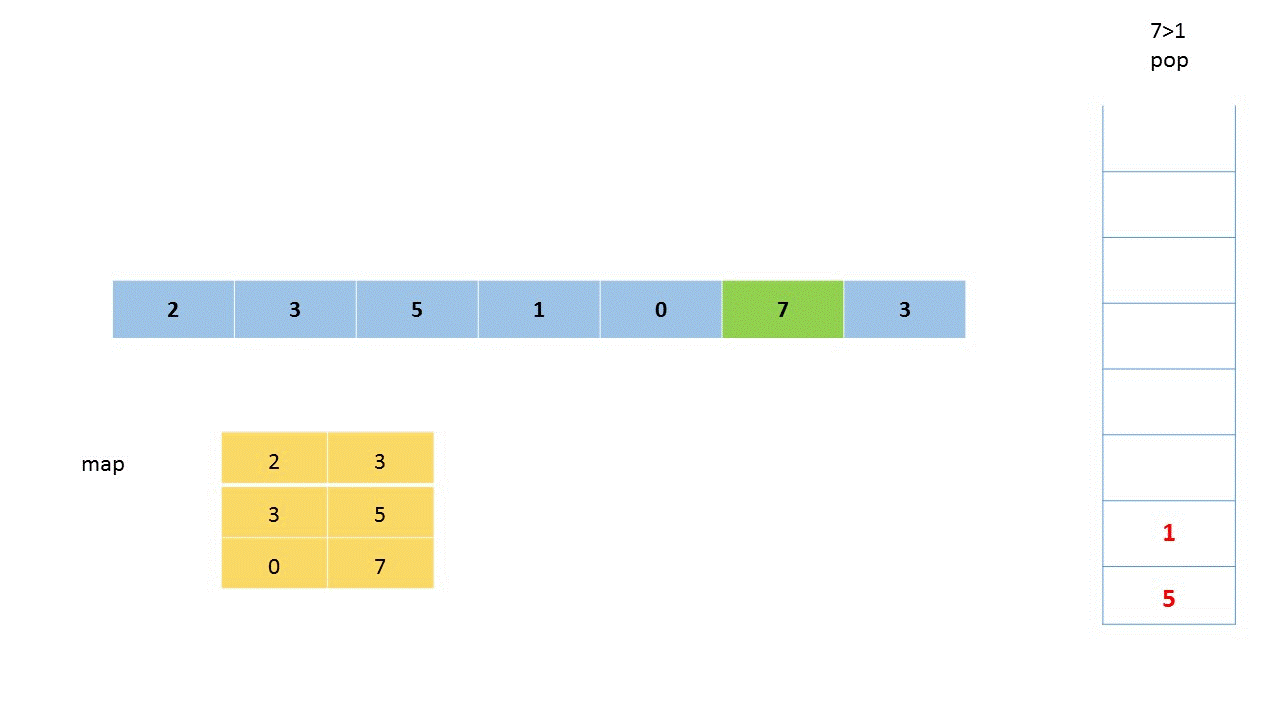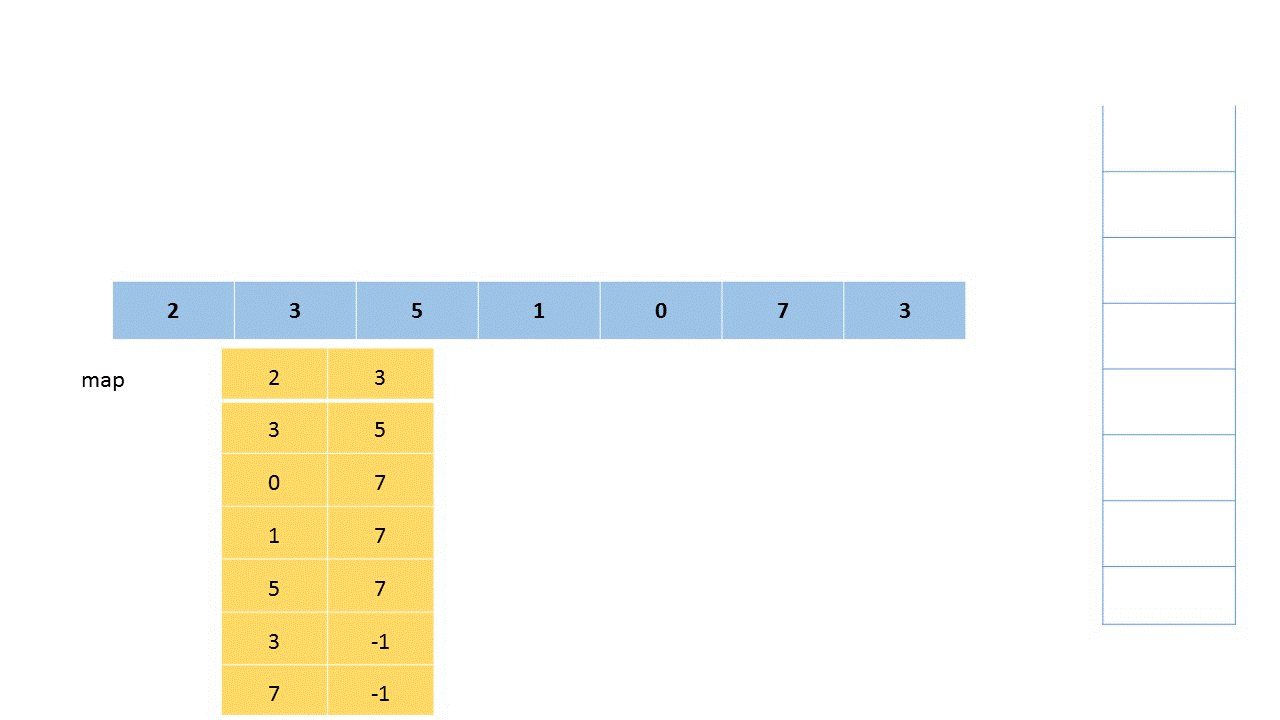
单调栈+HashMap

class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
    int[] res = new int[nums1.length];
    Stack<Integer> s = new Stack<>();
    HashMap<Integer, Integer> map = new HashMap<>();

    for(int i=0; i<nums2.length; i++){

        while(!s.isEmpty() && s.peek()<nums2[i]){
            map.put(s.pop(), nums2[i]);
        }
        s.push(nums2[i]);
    }

    while(!s.isEmpty()){
        map.put(s.pop(), -1);
    }

    for(int i=0; i<nums1.length; i++){
        res[i] = map.get(nums1[i]);
    }

    return res;

}

}

时间复杂度：O(M+N)，其中 M 和 N 分别是数组 nums1 和 nums2 的长度。

空间复杂度：O(N)。我们在遍历 nums2 时，需要使用栈，以及哈希映射用来临时存储答案。

6. 棒球比赛（leetcode-682）

你现在是棒球比赛记录员。
给定一个字符串列表，每个字符串可以是以下四种类型之一：
1.整数（一轮的得分）：直接表示您在本轮中获得的积分数。
2. "+"（一轮的得分）：表示本轮获得的得分是前两轮有效回合得分的总和。
3. "D"（一轮的得分）：表示本轮获得的得分是前一轮有效回合得分的两倍。
4. "C"（一个操作，这不是一个回合的分数）：表示您获得的最后一个有效回合的分数是无效的，应该被移除。
每一轮的操作都是永久性的，可能会对前一轮和后一轮产生影响。 你需要返回你在所有回合中得分的总和。 

示例 1:
输入: ["5","2","C","D","+"]      输出: 30
解释:
第1轮：你可以得到5分。总和是：5。
第2轮：你可以得到2分。总和是：7。
操作1：第2轮的数据无效。总和是：5。
第3轮：你可以得到10分（第2轮的数据已被删除）。总数是：15。
第4轮：你可以得到5 + 10 = 15分。总数是：30。

示例 2:
输入: ["5","-2","4","C","D","9","+","+"]      输出: 27
解释:
第1轮：你可以得到5分。总和是：5。
第2轮：你可以得到-2分。总数是：3。
第3轮：你可以得到4分。总和是：7。
操作1：第3轮的数据无效。总数是：3。
第4轮：你可以得到-4分（第三轮的数据已被删除）。总和是：-1。
第5轮：你可以得到9分。总数是：8。
第6轮：你可以得到-4 + 9 = 5分。总数是13。
第7轮：你可以得到9 + 5 = 14分。总数是27。

注意：
输入列表的大小将介于1和1000之间。 列表中的每个整数都将介于-30000和30000之间。 

Related Topics 栈

栈

在处理数据时保持栈上每个有效回合的值。栈是理想的，因为只处理涉及最后或倒数第二轮的操作。

栈实现棒球比赛

class Solution {
public int calPoints(String[] ops) {
    Stack<Integer> stack = new Stack<>();
    int res = 0;

    for(String s : ops){
        if("C".equals(s)){
            stack.pop();
        }else if("D".equals(s)){
            stack.push(stack.peek()*2);
        }else if("+".equals(s)){
            int t = stack.pop();
            int newT = stack.peek() + t;
            stack.push(t);
            stack.push(newT);
        }else{
            stack.push(Integer.valueOf(s));
        }
    }

    while(!stack.isEmpty()){
        res += stack.pop();
    }

    return res;
}

}

7. 比较含退格的字符串（leetcode-844）

给定 S 和 T 两个字符串，当它们分别被输入到空白的文本编辑器后，判断二者是否相等，并返回结果。 # 代表退格字符。
注意：如果对空文本输入退格字符，文本继续为空。 

示例 1：
输入：S = "ab#c", T = "ad#c"            输出：true
解释：S 和 T 都会变成 “ac”。

示例 2：
输入：S = "ab##", T = "c#d#"            输出：true
解释：S 和 T 都会变成 “”。

示例 3： 输入：S = "a##c", T = "#a#c"            输出：true
解释：S 和 T 都会变成 “c”。

示例 4：
输入：S = "a#c", T = "b"            输出：false
解释：S 会变成 “c”，但 T 仍然是 “b”。 

提示：
1 <= S.length <= 200
1 <= T.length <= 200
S 和 T 只含有小写字母以及字符 '#'。 

进阶：
你可以用 O(N) 的时间复杂度和 O(1) 的空间复杂度解决该问题吗？ 

Related Topics 栈 双指针

1）双指针（推荐）

一个字符是否属于最终字符串的一部分，取决于它后面有多少个退格符。

如果反向遍历字符串，就可以先知道有多少个退格符，然后知道退格符左边有多少个字符会被删除，对应的也就知道哪些字符会保留在最终的字符串中。

双指针比较字符串

class Solution {
public boolean backspaceCompare(String S, String T) {
    int i = S.length() - 1, j = T.length() - 1;
    int skipS = 0, skipT = 0;

    while (i >= 0 || j >= 0) { // While there may be chars in build(S) or build (T)
        while (i >= 0) { // Find position of next possible char in build(S)
            if (S.charAt(i) == '#') {skipS++; i--;}
            else if (skipS > 0) {skipS--; i--;}
            else break;
        }
        while (j >= 0) { // Find position of next possible char in build(T)
            if (T.charAt(j) == '#') {skipT++; j--;}
            else if (skipT > 0) {skipT--; j--;}
            else break;
        }
        // If two actual characters are different
        if (i >= 0 && j >= 0 && S.charAt(i) != T.charAt(j))
            return false;
        // If expecting to compare char vs nothing
        if ((i >= 0) != (j >= 0))
            return false;
        i--; j--;
    }
    return true;
}

}

时间复杂度：O(M + N)，其中 M, N 是字符串 S 和 T 的长度。

空间复杂度：O(1)。

2）重构字符串

构造函数（使用栈）去除退格符和被删除字符后的字符串，然后比较它们是否相等。

栈比较字符串

class Solution {
public boolean backspaceCompare(String S, String T) {
    return build(S).equals(build(T));
}

public String build(String S) {
    Stack<Character> ans = new Stack();
    for (char c: S.toCharArray()) {
        if (c != '#')
            ans.push(c);
        else if (!ans.empty())
            ans.pop();
    }
    return String.valueOf(ans);  //（从栈底到栈顶）
}

}

时间复杂度：O(M + N)，其中 M, N 是字符串 S 和 T 的长度。

空间复杂度：O(M + N)。

8. 删除最外层的括号（leetcode-1021）

有效括号字符串为空 ("")、"(" + A + ")" 或 A + B，其中 A 和 B 都是有效的括号字符串，+ 代表字符串的连接。例如，""，"()"，"(())()" 和 "(()(()))" 都是有效的括号字符串。
如果有效字符串 S 非空，且不存在将其拆分为 S = A+B 的方法，我们称其为原语（primitive），其中 A 和 B 都是非空有效括号字符串。
给出一个非空有效字符串 S，考虑将其进行原语化分解，使得：S = P_1 + P_2 + ... + P_k，其中 P_i 是有效括号字符串原语。
对 S 进行原语化分解，删除分解中每个原语字符串的最外层括号，返回 S 。 

示例 1：
输入："(()())(())"            输出："()()()"
解释：
输入字符串为 "(()())(())"，原语化分解得到 "(()())" + "(())"，
删除每个部分中的最外层括号后得到 "()()" + "()" = "()()()"。 

示例 2：
输入："(()())(())(()(()))"            输出："()()()()(())"
解释：
输入字符串为 "(()())(())(()(()))"，原语化分解得到 "(()())" + "(())" + "(()(()))"，
删除每个部分中的最外层括号后得到 "()()" + "()" + "()(())" = "()()()()(())"。

示例 3：
输入："()()"            输出：""
解释：
输入字符串为 "()()"，原语化分解得到 "()" + "()"，
删除每个部分中的最外层括号后得到 "" + "" = ""。

提示：
S.length <= 10000
S[i] 为 "(" 或 ")"
S 是一个有效括号字符串 

Related Topics 栈

1）借用一个int值记录左右括号数量（推荐）

使用一个值记录左右括号的数量。

展示代码

class Solution {
public String removeOuterParentheses(String S) {
    StringBuilder sb = new StringBuilder();
    int level = 0;
    for(char c: S.toCharArray()){
        //下述三条语句顺序不可改变！
        if(c == ')') level--;      //（1）
        if(level>=1) sb.append(c); //（2）
        if(c == '(') level++;      //（3）
    }
    return sb.toString();
}

}

2）使用栈

遍历字符串，遇到左括号就入栈，遇到右括号就出栈，每次栈空的时候，都说明找到了一个原语，记录下每个原语的起始位置和结束位置，取原字符串在原语的起始位置+1到原语的结束位置的子串便得到原语删除了最外层括号的字符串，拼接，即可解出答案。

栈方法

class Solution {
public String removeOuterParentheses(String S) {
    StringBuilder ans = new StringBuilder();
    Stack<Character> stack = new Stack<>();

    int start = 0;// 初始化原语的起始位置
    int end = 0;// 初始化原语的结束位置
    boolean flag = false;// 标志每个原语

    for (int i = 0;i < S.length();i++) {
        char ch = S.charAt(i);

        if (ch == '(') {// 遇到左括号，入栈
            stack.push(ch);
            if (!flag) {// 遇到的第一个左括号，是原语的开始位置，记录下原语开始位置
                start = i;
                flag = true;
            }
        }

        if (ch == ')') {// 遇到右括号，出栈
            stack.pop();
            if (stack.isEmpty()) {// 当栈空的时候，找到了一个完整的原语
                end = i;// 记录下结束位置
                ans.append(S.substring(start + 1,end));// 去掉原语的最外层括号，并追加到答案中
                flag = false;// 置标志为false，往后接着找下一个原语
                start = end;// 往后找，再次初始化原语开始位置
            }
        }
    }

    return ans.toString();
}

}

9. 删除字符串中的所有相邻重复项（leetcode-1047）

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。在 S 上反复执行重复项删除操作，直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。 

示例：
输入："abbaca"      输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

提示：
1 <= S.length <= 20000
S 仅由小写英文字母组成。 

Related Topics 栈

1）栈（推荐）

可以用栈来维护没有重复项的字母序列：

• 若当前的字母和栈顶的字母相同，则弹出栈顶的字母；

• 若当前的字母和栈顶的字母不同，则放入当前的字母。

实现1

class Solution {
public String removeDuplicates(String S) {
    StringBuilder sb = new StringBuilder();
    int sbLength = 0;
    for (char character : S.toCharArray()) {
        if (sbLength != 0 && character == sb.charAt(sbLength - 1))
            sb.deleteCharAt(sbLength-- - 1);
        else {
            sb.append(character);
            sbLength++;
        }
    }
    return sb.toString();
}

}

实现2

class Solution {
public String removeDuplicates(String S) {
    Stack<Character> stack = new Stack<>();
    for(int i=0; i<S.length(); i++){
        if(!stack.isEmpty() && stack.peek().equals(S.charAt(i)) ){
            stack.pop();
        }else {
            stack.push(S.charAt(i));
        }
    }
    StringBuilder str = new StringBuilder();
    for (Character c : stack){ // 栈的for循环，从栈底开始？  用while循环遍历，要反转字符串
        str.append(c);
    }

    return str.toString();
}

}

时间复杂度：O(N)，其中 N 是字符串的长度。

空间复杂度：O(N)。

2）替换函数（不推荐）

可以用字符串自带的替换函数，由于字符串仅包含小写字母，因此只有 26 种不同的重复项。

将 aa 到 zz 的 26 种重复项放入集合中；遍历这 26 种重复项，并用字符串的替换函数把重复项替换成空串。

注意，在进行过一次替换之后，可能会出现新的重复项。例如对于字符串 abbaca，如果替换了重复项 bb，字符串会变为 aaca，出现了新的重复项 aa。因此，上面的过程需要背重复若干次，直到字符串在一整轮替换过程后保持不变（即长度不变）为止。

展示代码

class Solution {
public String removeDuplicates(String S) {
  // generate 26 possible duplicates
    HashSet<String> duplicates = new HashSet();
    StringBuilder sb = new StringBuilder();
    for (char i = 'a'; i <= 'z'; ++i) {
        sb.setLength(0);
        sb.append(i); sb.append(i);
        duplicates.add(sb.toString());
    }

    int prevLength = -1;
    while (prevLength != S.length()) {
        prevLength = S.length();
        for (String d : duplicates) S = S.replace(d, "");
    }

  return S;
}

}

10. 用栈操作构建数组（leetcode-1441）

给你一个目标数组 target 和一个整数 n。每次迭代，需要从 list = {1,2,3..., n} 中依序读取一个数字。 

请使用下述操作来构建目标数组 target ：
Push：从 list 中读取一个新元素， 并将其推入数组中。
Pop：删除数组中的最后一个元素。
如果目标数组构建完成，就停止读取更多元素。 

题目数据保证目标数组严格递增，并且只包含 1 到 n 之间的数字。 

请返回构建目标数组所用的操作序列。 

题目数据保证答案是唯一的。 

示例 1：
输入：target = [1,3], n = 3
输出：["Push","Push","Pop","Push"]
解释：
读取 1 并自动推入数组 -> [1]
读取 2 并自动推入数组，然后删除它 -> [1]
读取 3 并自动推入数组 -> [1,3]

示例 2：
输入：target = [1,2,3], n = 3
输出：["Push","Push","Push"]

示例 3：
输入：target = [1,2], n = 4
输出：["Push","Push"]
解释：只需要读取前 2 个数字就可以停止。

示例 4：
输入：target = [2,3,4], n = 4
输出：["Push","Pop","Push","Push","Push"]

提示：
1 <= target.length <= 100
1 <= target[i] <= 100
1 <= n <= 100
target 是严格递增的 

Related Topics 栈

遍历[1~target的最大值]

遍历[1~target的最大值]，并与target内的元素比较，若target内存在该元素，则只有Push操作，若不存在，则Push操作后又执行Pop操作。

展示代码

class Solution {
public List<String> buildArray(int[] target, int n) {
    List<String> str = new ArrayList<>();
    int len = target.length;
    int maxv = target[len-1];
    int j=0;
    for(int i=1; i<=maxv && j<len; i++){
        if(target[j] == i){
            str.add("Push");
            j++;
        }else{
            str.add("Push");
            str.add("Pop");
        }
    }
    return str;
}

}